fe=0

S[i*( (<-v)v))+

+M(u,A(i-i-v)i);

и

где

-Mt (v-J) + Mv) +

(-1)*

ft=0

*(v ())

(6.70)

(6.70)

\((l-Y)-) = (-)-((l-Y)f). tAvM(-v))=4-)-4(l-V)l).

Ау/г

Вычисление годографов /i(cu) и /(cu) no /г(0 и w{t), если Y = const, производится тем лее способом, что и ранее (при Y=1). Разница состоит в том, что вместо разностей А^ /г(0) и Д^ ш(- вычисляются разности А^(Душ((1-V)-)];

Д'(Д, ,()) Д'(Д^((1-У))),Д'(()).

Определение годографов J\ (ю), (а ) по передаточной функции линейной части системы. Аналогично предыдущему, производя суммирование в выражениях. /, (со), /(сй), полученных выше можно найти представление /, (со), 1 (со) в явной форме через параметры (и полюсы) передаточной функции линейной части системы W{p). Для этой цели вычисляем при помощи (6.31):

Vi(-v)f) = (fe-)-{(fe-Y)-)==

A/(*i)-*((* + 0-A(*i)-

Подставляя эти значения в (6.69) и (6.69), после преобразований, подобных проделанным выше, найдем:

/, (ю) = -

(6.71)

1 +e

/(<o) находится аналогично:

/ ((й) = -p

P..V -

±

(Pv)

Zi Q(Pv)

(6.710

Эти выражения справедливы, когда полюсы передаточной функции

Р' Qip)

отличны от нуля и не равны друг другу. При наличии одного нулевого полюса

Q(p) = Qi{p)p

предельным переходом получаем /, (ш) = - ftp

1 +е

+ /

Ql(0) 2CD QUpv)Pv , . Ру-=-

I +е

(6.72)

/у (со) == - ftp

P V -

2Ш , q;(p,);,

(6.72)

При наличии двух нулевых полюсов

предельным переходом из (6.72) и (6.72) находим

/, (fi)) = -,

2©

Р (0) iL + У P(Pv) е -е Q.,(0) 2(0 Q2(Pv)Pv .

/ p (p) \ Я . Y P(pv)

rfpU2(p)jp=o 2C0 Q(p,)/

/.v- Pvn-v,-=.

I -1-е

(6.73)

v(<u)=ft

n-2 p V -

) V J V P(Py) - I

QaCO) 2co

C2(Pv)Pv

/P(P)\ ... у P(Pv) rfpW2(p)jp=o2co£ Q(p,)p

l-l-e PvV-

P -

. (6.73)

в общем случае, при наличии кратных полюсов, аналогично предыдущему получим

/, ((о)= -fep

v=0 11=0

. dp

/vl /vO-V.l\

v=0 n=o

111 dpi

и ±0 .±n 1 Pv

/V15- /v -v-

(6.74)

v=0 11=0

\ l+e-/

/ я \

(6.74)

v=0 n=0

Как видно из приведенных выражений, наличие зоны нечувствительности усложняет расчеты, поскольку теперь необходимо определить не одну величину, со, а две: со и у.

Если в линейной части системы имеет место запаздывание, то

(6.75)

Аналогично тому, как это было сделано в § 6.2, можно получить выражения для годографа релейной автоматической системы в этом случае. Они будут иметь вид

/j(C0) = (-I)fc

1 VI Р (ру) -р„т е

SUA Qi

Ру +-- /у + -5-

м Q(Pv)

IZi Q(p)p

l + e Py +-V-=- /y +l>-

для интервала /-со<(/ + у)- и

1+е

(6.76)

/, (a))=.(-l)+fc

CD Q (pv)

v=

;У P(Pv

Pv -v>v+/v + -

Pv +2-V)- . Py +1)

(6.77)

для интервала (/+ y)-J-<m <(/+

(0 Q (Pv)

, . у P(Pv) -PyT

1 +e

1 +e

(6.760

для интервала (/-1 + y)-7<m</-,

J V ZlPvLp-Pv-i

a Q (Pv)

P(Pv) g-PvtA

Q (pv) Pv

(6.770

для интервала - со (/+ y) 7-

Если передаточная функция линейной части имеет один нулевой полюс, т.е.

(6.78)

то предельным переходом из (6.76) - (6.77) получим годографы релейной автоматической системы для этого наиболее распространенного случая *):

/,(со) =

Со1 1 Y Р (Ру) -P t £

Pv +2-V) Pv - -

v Qi(Pv)Pv

v=l Р(0)

Qi (0)

,-1 P (pv) -Pvt £

v +2-V>i Pv + -

Q (Pv) Pv

Pv-

(6.79)

*) Cm. также Л. A. С л a в и p [!]

для интервала + v)- w + О

/, (co) = (-l)/jp

n-l Pv +-V>77 Pv + -77

® (Pv) Pv

P(0) Я yi P (pv) -p,.T e - e

Q,(0) 2co Q;(Pv)Pv

Pv -

(6.80)

для интервала / < со < (/ + v) .

/ (со) = (-!)yfe Jiy P(Pv) g-Pyxe >-e

I+e

Q,(0) 2cu

q;(pv)pv

л

I +e

(6.79)

для интервала {I-I+у)а>1.

/,(C0) = (-1)/Jp

£oi 1 у P (pv) -p T e >,Qi(Pv)Pv

Pv +V)- Pv <+>-

I +e

P(0)

Ql (0)

[ V P (Pv) -P t e

zLl , Ч 2

Pv +V>l /V<+)

Ql(Pv)Pv

(6.80)

для интервала /-<co<(/-f у) -

При произвольном расположении элемента запаздывания в линейной части системы передаточная функция ее может быть представлена в форме

1Г(р) = 1Г,(р) + 1Г2(р)е-р-

и для определения годографов релейной системы /i(co) и 1у{а>) следует применить выражения /i(co) и /(со) при г = О и т =7 О, приведенные в этом параграфе.

§ 6.4. Годографы релейных систем с несимметрией

Для релейных автоматических систем с несимметричной характеристикой релейного элемента, обладающей гистерезисом (без зоны нечувствительности), годографы /i(co) и /(со) имеют вид (6.9):

т f \ I ~-( 2я\ . / 2я\

(6.81)

Задаваясь значениями сое(0, оо), построим для различных

jlml,(u)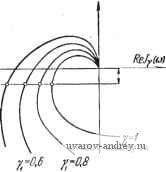

Рис. 6.16. Семейство годографов /j (и) и /у (со) параметра Y и прямые -f + и +у (0)

-fn- o+Jo o

значений у годографы /i(to) и /у(со) (рис. 6.16). Проведем на плоскости J\ прямую - fn -f Ио + .+ 2/oUo(0), а на плоскости /у - прямую - fn -xo + f/o1o(0). Как и ранее, в точках пересечения первой из этих прямых с /i((o), находящихся в правой полуплоскости, и второй прямой с /у(со), находящихся в левой полуплоскости, определяем значения со, соответствующие различным значениям Yi- Строя зависимости yi - Ti (со) и Yi = Гу(со) (рис. 6.17), находим возможные частоты автоколебаний со и соответствующие им значения Yi, в точке пересечения кривых Ti и Гу.

Для этих значений со и yi, как следует из рис. 6.16, выполняются условия

Im/,(co) = -/n + Xo + i/oWo(0), Re/,(co)>0 (6.82)

Рис. 6.17. Определение параметров ав-токоле5аний ю и V по кривым Г| и Г^.

Im 1у(со) = -Г„-щ> + yoWo (0), Не/(со)<0,

(6.83)

что совпадает с условиями существования автоколебаний (5.74), (5.74).

jImlM

Рис. 6.18. Го.п,ографы /j (и) и Sy ((о) при Y=const и прямые -f + -1-г„, -fn-Ид+гд. К определению зависимостей Zg=rj (и), г^Ту (т).

Если же линейная часть нейтральна, то для определения несимметричных автоколебаний нужно воспользоваться годографами (6.10)

/. (со) = - 4 () - /2 {-).

( ) = - i (y, ) - /2 (v. ) .

(6.84)

где Yi - фиксированная величина. Построим при фиксированном зна-Ъ чении Yi и (ое(0, оо) годографы /i(co) , и /((о) (рис. 6.18) и. проведем на пло-

Рис. 6.19. Определение парамет г^ р , ,

ров автоколебаний (о и г„ по СКОСТИ ПрЯМуЮ -/п i Хо2о, а На кривым г, и Гу. ПЛОСКОСТИ /у- ПрЯМуЮ - fп - Хо-f о.

В точках пересечения при заданных хо, fn находим для различных значений го соответствующие значения соо. Определяя по этим данным зависимости го = Г1((о)и 2о = Гу((й) (рис. 6.19), находим возможные частоты автоколебаний (d и соответствующие им смещения го.

Годографы релейной системы можно вычислить, как и ране.е, по частотной или переходной характеристикам или передаточной функции линейной части. Мы ограничимся здесь получением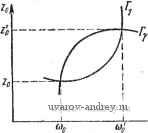

годографов релейной системы, определяемых по частотным характеристикам и передаточной функции.

Определение годографов /1(01) и /у(ш) по частотной характеристике линейной части. Рассмотрим сначала случай устойчивой (не нейтра. 1ьной) линейной части системы.

Воспользуемся выражением 2, {t) (5.70)

g,(0 = ftp{(2Y,-l)iro(0) +

+ S S sin У|Яг cos [rco - ryin + Q (m)]

Производная 2, (t) no t равна 4fe

Zi () = - CO ~ Wo (m) sin YiW sin [rcof - гу,зт -f 6 (rco)]. Учитывая, что

получаем после обычных преобразований

2 [(1 - COS 2гу,л) t; (rco) -f sin 2rY,nF(rco)] - - -

(2y. - 1)1Го (0) + Jl! (rco) - -7- 1/ (rco)

(6.85)

vW-i r(v,f)-a(v,)=

2fe,

[(1 - COS 2rY,n) и (rco) - sin 2гу,я(rco)] --Ц^ -

1 /-=1

- /[(2y - 1)f ITo (0) -f V p-M f/ l-cosryin (

(6.850

Отметим, что теперь годографы /i(co), с ростом © стре-

мятся не к нулю или действительной постоянной, а к /(2у1 - l)Wo(O). Если линейная часть системы нейтральна (Uo(0)=oo), то вместо Zi{t) (5.70) нужно воспользоваться 2(0 (5.81)

4kp -г^ Wo {ГШ)

2 (О = 2-г- Yi ~ Yi + 6 ( )]-

Го (лсо)

Производная 22(/) совпадает с производной 5i(/). Следовательно, вместо (6.85) и (6.85) в этом случае мы получаем

AM=-ti-()-ft(f)-

= 5] [(1 - cos 2гу,я) (У (га) -f sin 2,-у,я V (ш)]

. v Г sin 2rYi3t f, , ч 1 - cos 2rYin , ч1 I /с

~ 2j L-г ()--;- ()J j (6.86)

)-/.2(y,

to J

V [(1 cos 2гу,я) и (2co) + sin 2гу,яУ (rco)] + -

i!£l!£L uirco)- F (ra)] . (6.86)

Определение годографов /i(co) и /y(w) по передаточной функции линейной части. Если передаточная функция устой-

чивой линейной части W{р)=

Р(Р) Q(P)

имеет простые полюсы.

отличные от нуля, то выражения годографов /j (со) и /(со) будут иметь вид

/, (со) = - 2kp

li О'

(О Q (pv)

I -e

1 / V (Pv) Zi Q(Pv)

vC-v.)!

I -e

v CO

(6.87)