график годографа / (со) при изменении со от О до оо, построенный по формуле (6.56) при ко - 1, изображен на рис. 6.12 сплошной линией.

Изменение ко приводит к изменению масштаба, а изменение 7м меняет оцифровку со годографа /(со).

Предположим, что переходная характеристика h{t) и импульсная характеристика w{t) заданы графиками рис. 6.10 или.

3 о

Рис. 6.10. Переходная характеристика h (i) {а) и ее производная к [t)=w (t) (б) линейной части следящей системы.

i и

Рис. 6.11- Действительная U (и) (о) и мнимая V (и) (б) части W (/и).

что эквивалентно, таблицами 6.2, 6.3. Для определения искомых разностей проще всего пользоваться табличным способом. Пусть

=1,57, т. е. со = 2. Выписывая в первых столбцах значения

h(t) и w{t)== li{t) при t - k, находим разности двух следующих друг за другом чисел. Проделывая то же самое с каждым столбцом, как это было описано выше, находим

д'+/г(0).

указанные в таблицах 6.2 и 6.3 жирным шрифтом.

Вычисление по этим данным годографа /(со) (6.29), если в нем ограничиться шестью членами, приводит к следующему значению:

/(2) = -0,320-А ИЗ,

JM(6)) ReM)

\-D,8

Рис. 6.12. Годограф релейной следящей системы / (и), вычисленный различными способами:-по передаточной функции (точные значения)---по частотной характеристике.

-0,8\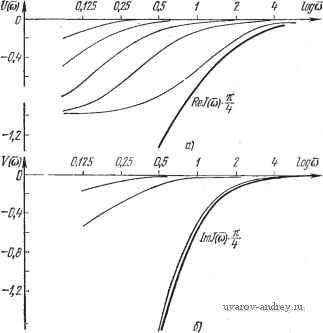

Рис. 6.13. Построение действительной Re / (и) и мнимой Im / (и) частей (-одографа / (со по действительной V (и) (а) и мнимой V Щ (б) частям частотной характеристики.

которое показано точкой с йо = 2 на рис. 6.12. Как видно из сопоставления, в выражении (6.29) нужно учесть шесть членов, чтобы получить достаточную точность. Следует отметить, что этот способ вычисления /(о) требует знания не только переходной, но и импульсной характеристики, и приводит хотя и к принципиально простым, но все же к длительным вычислениям.

Предположим теперь, что заданной является частотная характеристика линейной системы (см. рис. 6.11).

Пользуясь описанным выше способом построения годографа /(со), смещаем f/(co) и У(со) на 1,6; 2,3; 2,8; ... октавы; уменьшаем ординаты V[{2m- 1)й] в 2т - 1 раз и суммируем ординаты полученного семейства кривых при одних и тех же значениях й (рис. 6.13). В результате находим графики действительной и мнимой частей -/(й), показанные на рис. 6.13 жирными

линиями. Годограф /(со), построенный по этим данным, изображен на рис. 6.12 пунктиром. Совпадение его с точными значениями достаточно хорошее.

§ 6.3. Годографы релейных систем с зоной нечувствительности

При наличии зоны нечувствительности симметричные автоколебания характеризуются уже не одной, а двумя величинами - частотой со и относительной длительностью у. Для фактического определения этих величин воспользуемся введенными в § 6.1 годографами релейной системы /i(co) и /у((о), которые являются функциями частоты со и параметра у.

Задаваясь различными значениями со, построим для фиксированных значений параметра у (0<.у^1) годографы /i(co) и /у(со) (рис. 6.14,а,б).

Проведем на плоскости /i прямую -Хо, а на плоскости /у - прямую Кщ, где К - коэффициент возврата (при отсутствии гистерезиса Я, равно единице). Часто целесообразно годографы /i(co) и /у(ю) изображать на одной плоскости, как это показано на рис. 6.14, е.

В точках пересечения прямых -ко и Кко с годографами /[ (со) и /у(со) в левых полуплоскостях определяем значения со, соответствующие значениям у, т. е. находим зависимости у = Г] (со) и У = Гу(со), которые в виде кривых изображаем в системе координат у, со (рис. 6.15). Точки пересечения этих кривых и определяют частоты автоколебаний со, со и соответствующие им значения Yo и Yo-

Действительно, для этих значений со = сОд и со = со , как это следует из построения рис. 6.14, одновременно выполняются

j1 } 0.8 YD.6

\ ReJyia)

ReJ(o)

Рис. 6.14. Семейство годографов /i(a)) и 1у((л) параметра V и прямые -и К определению зависимостей V=ri (и), y=Vy (и).

Рис. 6,15. Определение параметров автоколебаний и и у ПО кривым Т\: и Г^.

следующие условия:

Im/, (со) = - Ко, Re /, (со) < О

} . (6.57)

1т/у(ш) = Яко, 1

Re/,(co)<0, } (-

что на основании определений годографов релейной системы (6.5), (6.6) и равенства z(t)= -x(t) совпадает с условиями существования автоколебаний (5.41), (5.41).

При этом, конечно, необходимо, чтобы выполнялось и третье условие: отсутствие дополнительных переключений релейного элемента (5.43). Это условие автоматически проверяется при построении формы автоколебаний.

Годографы релейной автоматической системы /i(cu) и /у((й), как и в предшествующем, более простом, случае можно вычислить по частотной характеристике, временным характеристикам или передаточной функции линейной части системы.

Определение годографов /1(0 ) и по частотной харак-

теристике линейной части системы. Воспользуемся выражением (5.14):

(0 = i-gsin(2m-l)vfX

X cos [(2m - 1) (0 - (2m - 1) Y - + е ((2m - 1) (о) .

Производная этой величины по t равна

(0=-ш^ Wo[(2m- l)(o]sin(2m-l)YX

X sin [(2m - 1) (0 - (2m - 1) Y + e ((2m - I) to)

Для реле с зоной нечувствительности величина скачка на выходе равна fep, в отличие от 2fep для реле без зоны нечувствительности. Поэтому соотношения, аналогичные (5.24) и (5.31), принимают вид

- (0) = - (0) + Kh (0), (т) = - г = - + i

Пользуясь этими равенствами (при /г(0) = 0), находим

1л\ **р V М^[{2т - I) со] . ,о 1\ и ЧУ

Xcos

(2m - 1) у - G ((2m - 1) to) , (6.59)

г-(-) = -2-{0)==- (0) + 4- (0) =

= -<й^ S Г[(2т- l)Q]sin(2m-l)Y-yX X sin f (2m - 1) у - G ((2m - 1) (0)1 + -i ргг) (0). (6.59)

2 -P

Принимая bo внимание очевидные тождества

(2m-l)Y-f--e((2m-l)(o)

= cos (2m - 1) Y -f-. cos G ((2m - 1) со) +

+ sin(2m-l)Y---sine((2m- l)(o).

(2m- i)Y---G((2m-l)(o)

=sin(2m-1)yy )) -

- cos (2m - 1) Y sin 6 ((2m - I) (o),

и обозначения мнимой и действительной частей (6.16), получаем после элементарных преобразований согласно (6.5)

1т/,((о)=.-г()== S [£ 2т-1)(о) +

+ ~°;f;i7 F((2m-l)co)] (6.60)

и

ReA((o) = -±-(-.) =

2 [(1 - cos(2m-l)Yn)f/((2m-1)(о) -

- sin(2m -1)уяГ((2т- 1)сй) --;ш(0)}. (6.60)

Следовательно,

/,( ,)==-(0) + 5]{[l-cos(2m-l)YK]f/((2m-l) )-

sin(2m -l)ynV((2m - 1) ) + /[linigjlvt ((2; - 1) ) +

l((2m -1) (o)]}. (6.61)

1 - cos (2m - 1) yrt 2m- 1

Полагая в выражениях Для z{t) и z(t) величину t равной у- , после аналогичных преобразований получаем

{(1 -COS (2m - 1) yot) f/ ((2m -1) (o) + + sin(2m-l)ynV ((2m - 1) ) -; [ (2;-и((2m - 1) )-

-~lm-7 ((2-) )]}- (6.62)

Для вычисления годографов /i( >) и /((u) целесообразно воспользоваться следующими соотношениями, вытекающими из (6.61) и (6.62):

/+==1 [/,( )+ /,( )] =

fen . 2Й

- te; (0) + 2 (1 - cos (2m - 1) yk) X

X[f/((2m-l)a>) + yi £

(6.63)

/- = I [/,( )-/,( )] =

(6.64)

Вычисление /+ и / можно производить следующим образом.

Задаваясь значением y> находим по таблицам значения 1-cos (2т- 1)yk и sin (2т- 1)y для различных т.

Эти значения определяют масштаб действительных и мнимых частей частотной характеристики. Дальнейшее построение сводится к тем же операциям, которые были описаны в предыдущем

параграфе, с той лишь разницей, что вместо U{(2m-1)(в) и Г((2т-1)(в) используются

(1 -cos (2m-1) yjt) и ((2m-1) to), (1 -cos (2m- 1) ул) V((2m-l)a), (sin (2m - 1) yn) и ((2m - 1) to), (sin (2m - 1) yn) V ((2m - 1) со)

соответственно.

Находя /+ и / , определяем /(со) и /(со) из очевидных соотношений *)

/, (со) = /+ + / , I /Лео) = /+-/-. I

(6.65)

При больших значениях со обычно t/(co) и V(co) стремятся к нулю.

Пренебрегая в (6.63) и (6.64) значениями (/((2т-1)со) и V{{2m - 1)со) при m > 1, найдем приближенные выражения для /+ и / в виде

- V sin ynW (/со).

(6.66)

Следовательно, при больших значениях со

(\~ e-i-) W (/со) -w)==

-w(0)---sinv-Wo(co)e

e( i)-{i+v)Y

(6.67)

и

(i - ey) W ij(0)---wiO) =

- 4 ,0) + s, v WMe [ - - l. (6.68)

Если гг>(0) = 0, то /Дсо) и /.(со) отличаются в этом случае от частотной характеристики Ц7(/со) наличием комплексного множителя ~{1 - е^1У').

*) Графоаналитический способ построения годографа /i(co) и /у(со) опи-сан Л, П. К у 3 ь м и н ы м [1].

Определение годографов /,(( ) и /(ю) по переходной характеристике линейной части системы. Воспользуемся для этой цели выражениями (5.16) и (5.16):

и

z(t) = kp{-l)A,h{t+ik-y)), yt.

где

Mt + (k-y))h(t + k)-,(t + (k~y)). производная z(t) по t определяется выралсениями

(t) + S (-l)\w(t+(k-y), Oty

причем первое из них дает z~ (у - левое значение в точке = Y-, а второе дает z~ (-j - левое значение в точке = -. Принимая во внимание, что

находим из выражения для z{t), справедливого в интервале 0<<Y- при = 0

Im J, (со) = - г (fj = g (0) = fep 5] (-1) Д,/г ((k -у)~). Из второго выражения для z(t) при 1 = - находим - Re/,W -l-(4) = i(-.,i,.((*-V)l).

Следовательно,

/,( ) = йр5] (-If [,w({k~y)) + iyh({k-y))]. (6.69)

\h(ik-y)]h(k)-h(ik-y)) и

Подставляя t = y- в выражения для z{t) и z{t), справед-

ливые в интервале 0</<у-. находим

1ш /VN == - (v ) = - S + (v )

и

Re/,(co) = --li-(Y) =

Следовательно,

= - I i (-1) A, -J) + /Д/ --)] +

+ i(v-) + /Mv)} (6.690

где

A(,i) = A((t + v)v)-.(*-b)

и

Д,г.(-)==ш(( + у)-)-(-).

Выражения (6.69) и (6.69) позволяют определить годографы релейной системы через переходную характеристику h(i) линейной части и импульсную характеристику w{t).

Воспользовавшись преобразованием Эйлера (6.26), аналогично предыдущему, выражения для /1(0) и /(сй) можно привести