или

i L v=I

2(й

P(Pv)

Q (pv) Pv 2(й

(6.42)

Выражения (6.41) и (6.42) справедливы для случая, когда полюсы передаточной функции W{p), т.е. корни уравнения Q(p) = = О, не равны друг другу и отличны от нуля.

Если уравнение Q(p) = 0 имеет нулевой корень кратности Го - 1, т.е. если

Q(p) = P -Qr,~i(p), Qr.-i{0)0,

то выражения для годографа /(ш) удобнее всего получить предельным переходом из (6.42). Так, при Го = 2, т.е. при наличии одного нулевого полюса у W{p), получим

/( ) = -ftp

fi-i

Si<3l(Pv)Pv 20)

fi-l

Q,(0)2o) Q;(p)p

(6.420

При Го = 3, т. е. при наличии двух нулевых полюсов у W {р), из (6.420 предельным переходом получаем

/( ) = -ftp + /

Р(0) п

02(0) 20) Q2(Pv)Pv 20)

Р{р) \ л , у Р (Ру)

rfp \Q2(p) J

20) Q

t;02(Pv)Pv 20) J

(6.420

Годографы релейной системы /(со) для приведенных выше трех случаях Го=1, 2, 3 можно записать в единой форме;

/(со):

Ру 2o)

где приняты следующие обозначения:

с

01 Q, (0)

(6.44)

Кроме того, в этой формуле с. и с!, как обычно, равны Р(Ру) г' -с о =-L(PyL (6 45)

a c определяется из (6.39).

Если значение ру, = а^ действительное, то вычисление

thip производится по таблицам гиперболического тангенса

W 0,8 0,6 0,4 0,1 О

л

16 ё

Рис. 6.8. График th

из Приложения 5 либо по графику th-, где й (рис. 6.8).

Изменение а., сводится к изменению масштаба й. Если - комплексно сопряженные корни

то соответствующие им коэффициенты с., с^, о(или с'., c+i.o) также будут комплексно сопряженными

VO = V0 + iKo v+I. о = vO -

Замечая, что

я (tty ± /Юу) (а о

2(й , 3tav , яю^ СП--h cos--

получим

= 2 о ..... -20

(О

СП--h cos-- ch---l-cos--

а ю ю о

Таким образом, каждая пара слагаемых в /(ш), соответствующая комплексным сопряженным полюсам р^, pv+i, может быть представлена в вещественной форме.

Однако для вычисления /(ш) (6.43) может оказаться более

удобным представление Cvo> v+i.o и th в показательной форме

Cvo = 1 voc+i.о =1

и

П (Су ± /СОу) Я(1 ± /Юу) ±

2(й 2ю ~~

Ov - О)

да v-. = - и

, я Ov

/ ch--cos я-=

Т| / о (й

f ch Н- cos я-

. Я

Sin -

Тогда

VI/ о^ V

о й

th-l- -bv+i.oth =2М, c,ocos(,-b#J.

Значения Mv и О'у можно определить по ©v и й при помощи графика, предложенного И. В. Пыщкиным (рис. 6.9).

Найдем выражение /(со) при больших и малых значениях и. Для этого воспользуемся (6.43).

Замечая, что при больших ш

th i!fv Ру Ру 2(0 ~ 2о 24а>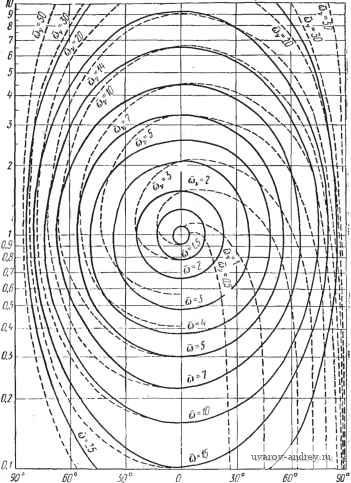

Рис. 6.9. График Пышкина; thn-

после элементарных преобразований получим

/ S \

-ftp]

v=l \

2(0 fv 24(йЗ

01 Г vOv v=l

(6.46)

При малых значениях со

th-=±l.

в зависимости от знака Rep. Поэтому после преобразований будем иметь

П

01 2(й

. (6.47)

если линейная часть нейтральна, или

J v=l

(6.48)

если линейная часть устойчива.

(При Cq, Ф о (т. е. Гц = 3), слагаемыми под знаком суммы в формуле (6.47), уместно пренебречь.)

Нетрудно установить связь этих приближенных выражений /(со) с выражениями (6.21) и (6.2Г). В самом общем случае, когда W (р) = Р (р)/Q (р) имеет кратные полюсы:

ро=0 кратности Гв-1, pi=0 кратности Ги

Ps - 0 кратности rs,

Причем Го- 1 + Г] + + = /г, где п - степень знаменателя передаточной функщш, переходная характеристика определяется по формуле разложения для кратных полюсов (см. Приложение 1 и § 2.2)

v=0 (1=

(6.49)

где

P{p) Q{p)P

ip-рГ

(6.50)

Подставляя (6.49) в (6.24) и (6.24) и проделывая под знаком производной -- выкладки, аналогичные предыдущим, полу-

чим для этого общего случая выражение годографа релейной системы

/((в) = -

v=0 n=0

fl dp

(6.51)

где с', как и ранее, определяется соотношением (6.39). Из выражения (6.51) могут быть получены приведенные выше частные случаи. Для непосредственных вычислений (6.51) слишком громоздко.

Приведенные выражения для годографа релейной системы справедливы лишь для того случая, когда линейная часть системы состоит из элементов с сосредоточенными параметрами.

Если в линейной части системы имеется элемент запаздывания, включенный так, что

(6.52)

то выражения годографа / (о) для этого случая примут иной вид.

Для вывода / (со) достаточно в (6.24) и (6.24) h{t)viw (t) заменить на h{t - x) и w(t - x) и учесть, что h(t-x) = w{t - x) = 0

при t<x. Тогда (6.24) и (6.24) при (/- 1)-< т < запишутся в виде

1т/(со) = -йр ( 1)*дл(й^-т), (6.53)

k=i-\

Re/(fi.)==-&p 5] ( 1)*ди,(й- т). (6.53)

Вычислим Д/г(0 и Ам;(0= Д/г(0 при помощи (6.31): Л (-5-) - * (<* + - - * -I =

причем здесь k> I*).

Подставляя эти значения в (6.53), (6.53), меняя местами порядок суммирования и используя формулу суд1мы геометрической прогрессии, получаем

/(а)) = (-1)+ ftp

P(Pv)

Q (Pv)

2е

V Р (Pv)

.) Pv

1 +e

(6.54)

При (/--l)-< (u</-. При наличии нулевых корней уравнения Q(p) = 0, т. е. когда

Q(p) = p- -4.-.(P). Q,. , (0) Ф О,

*) При А = /. очевидно, ДА (/- - rj = л(/- - tj и Дю (/ --tJ =

предельным переходом из (6.54) при Го = 2 получаем

/(со) = (-1)+

P(pv)

Ql (Pv) Pv

1 +e

P(0)

Qi(0)

ra-l

v) Pv

1 +e

(6.54)

при (/-1)-5-<сй</.

Выражение /(со) для Го = 3 получаем предельным переходом из (6.54):

/(.) = (-!)-р{ + °

.(0)

Р(Ру) Q2(Pv)Pv

2е

Г 2 j ю;

1+е

dp \ Qs (Р)

Р (Ру)

Q2(Pv)Pv

2е

(6.54 )

при (/-1) -<со в этих формулах с'= ш(0), опреде-

ляется из (6.40).

Если в линейную часть системы входит элемент запаздывания, так что

(6.55)

m(o)=.IlSPLjLliM.e-Р'- Q{p) + Q{p)

то, чтобы определить годограф /(со), следует для каждого слагаемого в (6.55) использовать соответствующие выражения при т = О и т 0.

Выбор того или иного выражения для годографа релейной системы /(со) зависит от конкретных условий. В простейших случаях, когда полюсы передаточной функции легко определяются через параметры системы, наиболее удобно использовать

замкнутую форму /(со). В тех случаях, когда заданы, например, экспериментально снятые временные характеристики, можно воспользоваться выражением /( ) через переходную и импульсную характеристики. Наконец, если линейная часть системы сложна, содержит распределенные параметры, а отдельные звенья определены характеристиками, полученными экспериментально, наиболее быстро ведет к цели выражение /(со), содержащее частотную характеристику.

Пример построения годографа /(со). Для иллюстрации приведем вычисление годографа /(со), пользуясь различными выра-ражениями его для простейшей релейной следящей системы.

Передаточная функция ее линейной части согласно (2.106) при Гя = О равна

Qi (р) Р {ТмР + 1) р

где &л == дви- Переходная характеристика определяется выражением

Импульсная характеристика равна

w(t)=h(t) = k!\-~e ), ш(0)==с' = 0. Графики h{t) и w{t) = h{t) при Гм = 1 и йд = 1 изображены на рис 6.10. Численные данные h{t) и w{t) при = -. = 2 приведены во вторых столбцах таблиц 6.2 и 6.3. Частотная

ТАБЛИЦА 6.2

Вычисление разностей Д*й (0) при СО = 2

Вычисление разностей Д*гу j при ш = 2

характеристика линейной части получается при подстановке в W{p) значения р = /со, т. е.

Отсюда действительная и мнимая части будут равны f/(co) =--V(co) =---.

Графики f/(co) и Г(со) изображены на рис. 6.11.

Как видно из выражения передаточной функции W{p), ее полюсы равны

P\ - -j-. Ро = 0.

Вычисляем коэффициенты с^ с\, с,: Р(0) - Pf.

л' 10 п'/ \ л' - - -

Р(Р.) Ql (Pl) Pi

Qi (Pl) Pl

Подставляя эти значения в (6.42), находим

/(co) = -Mp{ith- + y(--r th-)}. .

Обозначая й = соГм и йо = л^рТм, запишем это выражение в виде

/(со) = th + / (- - th-) }. (6.56)