Действительная и мнимая части годографа на рис. 6.5 показаны жирной линией.

Описанное построение можно упростить, если частоты для иЫ) и 1(со) откладывать в логарифмическом масштабе (рис. 6.6). В этом случае кривые U[(2m - l)tu] и V[{2m - получаются простым смеще-

ием кривых U{a) и V((o) .....-

на 1,6; 2,3; 2,8; ... октавы. Напомним, что октава соответствует изменению частоты вдвое.

Если (как это обычно бывает) f/((o) и К((о) стремятся к нулю с ростом (О, то для больших значений ю из (6.18) получим приближенное выражение годографа /(со):

/(со)

4kr>

[f;(to) + /T(co)]=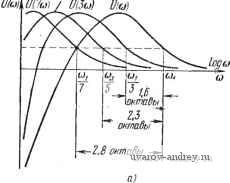

(6.19)

Рис. 6.6. Построение действительной Re / (о и мнимой Im / (со) частей годографа / (и) по действительной £/(и) (а) и мнимой К (и) (б) частям W в логарифмическом масштабе частот.

Отсюда следует, что на высоких частотах годограф / (со) совпадает с точностью до постоянного множителя

с частотной характеристикой линейной части системы. /

Следовательно, поведение /(со) при высоких частотах позволяет на основании результатов § 4.4 судить также и об устойчивости положения равновесия релейной системы.

С уменьшением частоты со число слагаемых в выражении для частотной характеристики (6.18), которые необходимо учитывать, возрастает, и при очень низких частотах вычисление по формуле (6.18) становится слишком громоздким.

Замечая, однако, что с уменьшением ш ряды Фурье, определяющие z{t) и z{f), стремятся к интегралам Фурье, можно воспользоваться этими последними для вычисления значений годографа /(со) при со, близких к нулю, если в этом есть необходимость.

Производя обычным путем предельный переход, получим для очень малых значений ю приближенные выражения для z{t) и

Мы рассмотрим здесь вкратце тот случай, когда линейная часть устойчива. При достаточно малых со из (5.13) предельньш переходом получаем

z{t)

-°-sin[v/ + 0(v)]rfv

(6.20)

и, значит, если z{t) непрерывна, то

Z (f) == - Wo (v) cos [vt + e (v)l dv.

(6.200

Производя замену переменных = у и полагая t-дем согласно (6.2):

1т/(а,) = -Ц-;---

ReJ(a) = -~z-{~)

7 п^о

м

sin

v + e

= -. наи-

dv, (6.21)

o(v ) cos[v + e(v-)

(6.210

По этим выражениям любым из приближенных способов вычисления интегралов можно найти приближенные значения 1гпУ((о) и Re У (о) при малых о*). Устремляя (о к нулю и замечая, что при этом Wo[v )-Wq{0)= и {0) и e(v--)->0, находим из выражений для 1т/(ш) и Re/((u):

lim Im / (ю) = - Apt; (0), lim Re/(и) = 0.

0)-*0 и- 0

Если же линейная часть релейной системы нейтральна, то при

ОО.

Im/(со)-* -оо, Re/((u)-

Эти выводы можно получить и из физических соображений. Периодическое воздействие частоты ш = О соответствует скачкооб-

*) Вычисление годографа /(ш) при малых значениях ш проще производить по формулам, приведенным далее. В основе этих формул лежит не ча-.. стотная характеристика, а переходная характеристика или передаточная функция линейной части системы.

разному воздействию на линейную часть системы. Определив при этом воздействии установившиеся значения z{t), т. е. z{t) jpjj -♦оо, найдем 1т/(ю) и Re/(a)) при ш = О, приведенные выше. При w(0) -fi{0) ФО для построения годографа следует вместо выражения (6.18) пользоваться выражением (6.17), т. е.

L W (0)

учитывать слагаемое - йр-

Величину w(0) можно определить также таблично или графически из выражения

и)(0) = й(0) = 4 t/((o)rf(o.

(6.22)

которое получается из (2.67) после дифференцирования h{t) по t при / = 0. в этом случае уже нельзя заключить, что первое слагаемое годографа /(и) совпадает с частотной характеристи-

кой Г(/(о).

Описанное выше построение годографа /(са) по частотной характеристике линейной части справедливо, очевидно, и для тех случаев, когда линейная часть содержит элементы с распределенными параметрами, элементы запаздывания.

Определение годографа /(©) по временным характеристикам линейной части системы. Воспользуемся ранее найденным выражением (5.17):

2 (О - ftp { А (О + £ (-1) АЛ (/ + (ft - 1) ) I Производная z{t) по / будет равна (О = ftp I а'(t) + £ i-Dw(/ + (fe 1) i) j.

o</<-.

где w{t)=h(t). При / = - это выражение дает левое значение производной, т. е. z~ -j. Привлекая теперь равенство (5.25) при А(0) = 0, найдем

Z = - g (0) = ftp 2 (-1АЛ (ft ]. (6.23)

fe=0

Полагая t=- в выражении z{t}, получим

- И -kjj;i-itw{k)+ {) f. (6.23-

Значит, согласно (6.2)

Im/(a)) = -fep5;(-l) h(k-).

Re,W = -i! ,(4) + S(-l)*A ,(ft-)

(6.24) (6.24)

Учитывая, что ш -j = Лш (0) + (0). последнему выражению можно придать другой вид

Re /(ш) =-= - 1 (0) + lw[k )\. (6.24 )

I ft=0 1

Отсюда искомое выражение годографа релейной системы будет равно

или, с учетом (6.24 )

ft=0

(6.25)

fe=0

+/5;(-1)аа(й^)

ft=0

(6.25)

Из выражения (6.25) видно, что вычисление годографа /(to) сводится к предварительному определению первых разностей

Д/г а^ ) = 0.1.2,... и последующему алгебраи-

ческому суммированию их.

Если h{t) и ш(t) заданы численными значениями, то искомые разности определяются известными табличными способами.

Если h{t) и w(t) заданы графически, то определение разностей наиболее просто производить следующим образом.

Положим f = - в h(t). Тогда для того, чтобы получить из

h -j функцию h [k -j, где 1 - целое число, нужно изменить масщтаб времени в k раз (рис. 6.7, а).

Изобразим на графике кривые ft(ft-j для ft= 1,2,3,... (рис. 6.7, б) и при заданном значении со = со] (или, что то же самое, при i ) проведем прямую параллельно оси ординат.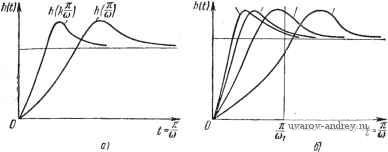

Рис. 6.7. Переходная характеристика (а). Определение разностей переходной характеристики для =- (б)-

Отрезки Прямой, заключенные между кривыми со значениями I и k, определяют величину и знак искомой разности

Аналогичным образом по кривой w{t)=li{t) можно найти

для любого значения ш. Подставляя найденные разности в формулы (6.25) или (6.25), находим значение годографа /(со).

Формулы (6.25) или (6.25) удобны для вычисления /(со), когда м{к- (а следовательно, и Aw(k~ с ростом к быстро стремятся к нулю.

Стремление ДЛ k -j к нулю будет иметь место, если линейная часть системы устойчива.

Для нейтральной линейной части системы при fe-*оо значение АЛ (ft -j стремится к постоянной величине. В этом случае,

а также в любом другом случае, чтобы ускорить сходимость рядов в (6.25), имеет смысл преобразовать (6.25) к более удобному для вычислений виду.

Для этой цели воспользуемся формулой преобразования Эйлера *)

fe=0

в этой формуле разность k-ro порядка равна

или

A4 = A gi-A go

к

(6.26)

(6.27) (6.28)

Полагая в формуле (6.26) gk равным поочередно и Аю(/г-~), получим выражение для годографа (6.25) в виде

г/ ч , I

Lft=0

ft=0

Вычисление /(со) по формуле (6.29) сводится к определению разностей (k-\-l)-ro порядка характеристики h{t) и ее производной-импульсной характеристики w{t), т. е.

В том случае, когда значения h{t) и w(t) заданы численно, эти разности можно вычислить известным табличным способом, который поясняется табл. 6.1.

Чтобы получить какую-либо разность в таблице, нужно из величины, находящейся непосредственно ниже и левее этой разности, вычесть величину, находящуюся непосредственно выше и левее.

Искомые разности Д^/г (0) и /S.w -j, входящие в формулу

(6.29), расположены в таблице соответственно по первой и второй нисходящим диагоналям.

Если h{t) и w{t) заданы графически, то, выделяя в них аналогично тому, как это делалось при построении процессов (см.

*) См., например, Б. Ван дер Поль и X. Бреммер [1].

Вычисление разностей Л*й j и (-j / = 0,1; = А ) = и.

.<.-.(.i) Л.(0(.А) д^)(,) дЗ,<,(,) д^и-,(.)

д/2(0)

Л..-. (2)

д^/,.-. ()

§ 3.2), линейно возрастающие составляющие, применяем к линейно возрастающей и ограниченной составляющим описанный

выше графический прием для определения АЛ k -j при k =

==0, I, 2, ... и ДЛ (/г= (ft--j при ft = 1, 2.....Зная эти

величины, находим Д^л(А- и Д^/г (ftj = Д^ю (ft-j и т. д.

Выражением (6.29) имеет смысл пользоваться лишь тогда, когда для вычисления годографа /(со) можно ограничиться небольшим числом слагаемых, т. е. для малых значений о (или

больших значений -j. В противном случае может оказаться

более удобным по h(t) построить предварительно li(/co), как это было упомянуто в § 2.2, а затем по W(/co) определить /(со).

Приведенные выше выражения позволяют, очевидно, построить /(со) и в том случае, когда IF (/со) или h{t) и w{t) получены экспериментально. Они справедливы для систем, имеющих линейную часть сколь угодно сложной структуры, содержащей как сосредоточенные, так и распределенные параметры.

Определение годографа /(ю) по передаточной функции линейной части системы. Если передаточная функция линейной части системы W{p) такова, что тем или иным способом можно найти ее полюсы, то годограф релейной системы /(ш) может быть определен через передаточную функцию (точнее, через полюсы передаточной функции) не в виде ряда, а в замкнутой форме.

Предположим, что W{p) представляет собой дробно-рациональную функцию от р, степень числителя которой меньше степени знаменателя, т. е. индекс которой положителен.

Если все полюсы простые и отличны от нуля, то, разложив W{p) на простейшие дроби, получим

Переходная характеристика, соответствующая этой передаточной функции, как было показано в § 2.9 (см. также Приложение 1), равна

Л(0 = Соо+Ес,оеЧ (6.31)

ft(0) = Coo+Sc,o = 0. (6.32)

В формулах (6.31) и (6.32) pv (v = 1,2, ...,n) представляют собой полюсы передаточной функции W{p), Cvo - коэффициенты, определяемые соотношениями (2.48) и, наконец, с'. = cqP.

Для получения годографа релейной системы /(ш) в замкнутой форме нужно просуммировать найденные выше выражения (6.17) и (5.25) для /(со).

Если используется формула (6.17), то из (6.30) при р =/ш находятся действительная О (а) и мнимая частотные ха-

рактеристики и используется для суммирования известное соотношение *)

4 а thi. . (6.33)

4 чг

Я 2,i;a2 + (2m-i)

При использовании формулы (6.25) из (6.31) при t - k. fe = l, 2, ... находятся hik-j, h{k~=w{k-Y а затем

*) См., например, И. С. Г р а д ш i е й н, И. М. Р ы ж и к [1].

д/г(й^ и Искомую сумму ряда можно найти,

использовав формулу суммы геометрической прогрессии.

Предоставляя возможность читателю применить первый из указанных способов суммирования для нахождения годографа /(и), мы здесь воспользуемся вторым способом. Вычислим первую разность/г (О (6.31),

M(,i)=,(,* + ,)i) (*i)=i;.y(/ -J ,)

и подставляя это значение в (6.24), получаем после изйенения порядка суммирования:

Im / (со) = - ftp i с,о (Л^ - l) Е (-1) Л' .

v=l й=0

Но по формуле суммы геометрической прогрессии -

i(-if

Следовательно,

h=0 IJ/V

Im /(со) = ftp 2j vo-

Принимая во внимание тождество

iL 20)

окончательно получаем

Im/(o)) = -ftp5]cvoth -

2о

Аналогичным образом, определив из (6.31) производную

(o=/i(/)=ic>4

да С = вычислим

At. (ft I-) = . ((ft + D-J-) - ( f) = V <o/ (/ - 1).

Подставляя Aw(k-] в (6.24 ) и проделывая выкладки, подоб-

\ СО /

ные сделанным выше (т. е. изменяя порядок суммирования и применяя формулу суммы геометрической прогрессии), найдем

Re/((u) = --

1 + е

или, с учетом (6.35),

Re/(co) = -

(6.38)

Re/(cd)можно представить, в зависимости от способа вычисления w{0), в различной форме. Так, полагая в (6.37) t = 0, получим

Подставляя это значение w{0) в (6.38), будем иметь

R,;w = :£<.(,+,higL). (6.38-)

Если же определить w{0) на основании теоремы о предельных значениях (Приложение 1, теорема 8) *)

w{0)= lim pL{w{t)} lim pW(p) = c, (6.39)

TO ИЗ (6.38) получаем

Re/(co) = -L Soth

2(й

(6.40)

Заменяя в (6.36) Cvo их значениями (2.48), a в (6.39) или (6.40) Cvo на Cvopv, получим выражения для годографа релейной автоматической системы в двух формах:

v=I v=I

(6.41)

*) Напомним, что здесь принято h(0) - 6.