Условия надлежащих моментов переключения:

==> о.

==-Хо.

(5.80)

Условие надлежащего направления переключения:

~(yi

о

о

>о, <о.

(5.800

При этом предполагается, что дополнительные переключения отсутствуют. Обозначим

Z2(t) = -~smyinr-sm[r(>iot - rytn + e{r(i)o)]. (5.81) /=1

Тогда согласно (5.79)

2(0==2о + 22(0-

Используя (5.72), запишем условия автоколебаний в виде:

22 Yl

СОо

- fп ~Ь Zq

r(Y.)>0.

(5.82)

(5.820

Теперь Yi - известная величина, определяемая выражением (5.77) Уравнения же (5.82) и неравенства (5.82) определяют значения частоты автоколебаний соо и смещения о. Естественно, что СОо и zo зависят от / .

§ 5.7. Автоколебания в связных релейных системах

Под связной релейной автоматической системой далее подразумевается релейная система, содержащая несколько релейных элементов.

Структурная схема связной релейной автоматической системы изображена на рис. 5.14.

Ограничимся здесь случаем релейных элементов без зоны нечувствительности. Обозначим через 2.,fe(/) установившуюся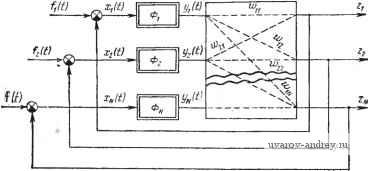

Рис. 5.И. Структурная схема связноП релейной автоматическоТ системы.

реакцию k-щ выхода линейной части релейной автоматической системы на периодическое воздействие s-ro релейного элемента, а через W ,{р), W,fe(/to)== . = 7 o(co)e fe , h,At\ соответ- Х. ственно, передаточную функцию, частотную характеристику и переходную функцию (s, k) - канала линейной части, т. е. канала между .s-m входом и k-u выходом. Очевидно, что

. (О =§2,0, fe = l. 2.....N,

(5.83)

где Zshif) определяется обычным образом (5.13), как реакция канала на последовательность симметричных прямоугольных импульсов, т. е.

2m- I

m==I

Рис. 5.15. Управ.1яющие сигна.1Ы в связной релейной автоматической системе.

X sinl(2m - 1) + е ((2т - 1) £о)].

(5.84)

При наличии в связной релейной автоматической системе периодического режима частоты соо каждая ошибка Xk{t) (/г = 1, 2, N) будет отличаться некоторым относительным сдвигом-фаз 0, а, aw, njDH4eM ai = О (рнс. 5.15. Учитывая эти

сдвиги фаз, можно записать условия существования простейших симметричных автоколебаний в виде совокупности условий существования смещенных друг относительно друга простейших колебаний. Таким образом, мы получаем:

условия надлежащих моментов переключения

Xk(- + ctk)=-ok, k = \,2,...,N, (5.85)

условия надлежащих направлений переключения

i?fe(-J+afe)<0, fe=l, 2, Л^, (5.850

и условия отсутствия дополнительных переключений xu{t) > - оь ak<t< + ak, ft = I, 2, .... Л/, (5.850

причем 1=0. В общем случае

4it)-=fk{t)-Zk{t), k\,2,...,N, (5.86)

а при отсутствии внешних воздействий

Xk{t) = -Zk{t), ft = 1,2.....Л^. (5.87)

Поэтому условия существования автоколебаний запишутся в виде

условий надлежащих моментов переключения

(~ + а.) = ft = 1, 2, ..., Л^, (5.88)

условий надлежащих направлений переключения

+afe)>0, ft=l, 2.....Л^. (5.880

При этом, естественно, должно выполняться и условие отсутствия дополнительных переключений (5.85 ). Условия (5.88) и (5.88) определяют частоту возможных автоколебаний ©о и относительный сдвиг фаз 2, 3.....0С№

Глава Vr

ИССЛЕДОВАНИЕ АВТОКОЛЕБАНИЙ В РЕЛЕЙНЫХ

АВТОМАТИЧЕСКИХ СИСТЕМАХ

§ 6.1. Годографы релейной системы

При исследовании автоколебаний и фактическом определении параметров автоколебаний важную роль играет понятие годографа релейной системы, которое позволяет дать наглядную интерпретацию условиям надлежащего момента и направления переключения.

Определим годограф релейной системы без зоны нечувствительности следующим образом:

Мнимая часть Im/(cu) годографа /(со) равна значению выходной величины линейной части системы z{t) при (с обратным знаком), а действительная часть Re/(co)-значению производной выходной величины линейной части системы z{t) при / =---О, отнесенной к частоте со (также с обратным знаком), т. е. производной 2 (/) по cof при t=- - О,

Таким образом,

Re/(co)-±r().

(6.2)

Годограф релейной системы без зоны нечувствительности полностью определяется поведением разомкнутой релейной системы при периодическом воздействии и имеет размерность выходной величины последней.

Для фиксированного значения со годограф релейной системы / (со) представляет собой вектор. При изменении со конец этогр вектора описывает кривую, каждая точка которой соответствует определенному значению со (рис. 6.1).

Иногда может оказаться полезным при --j Ф z-j рассматривать правый годограф релейной системы

/.W = -±i.(i) ;.-(i).

(6.3)

который дает представление о поведении системы непосредственно после скачка скорости. Однако, далее, если не будет специально оговорено, мы будем считать, что годограф релейной системы /(ю), определяется выражением (6.1).

При (-), оче-

/((о)-=У^((о). (6.4)

Рис. 6.1. Представление годографа релейной автоматической системы.

Для релейной системы с зоной нечувствительности в соответствии с увеличением числа условий существования автоколебаний введем два годографа, определив их следующим образом:

vM==-iH)-/>~(v-J).

(6.5) (6.6)

Эти годографы, 1]{а>) и Jy{(i>), являются функциями не только частоты ©, но и параметра у, изменяющегося в пределах от нуля до единицы. При у= 1 годографы /i((u) и /у((о) совпадают*).

Для анализа сложных автоколебаний введем семейство годографов:

/f(v -=-).

т = 1, 2,..., S- 1,

(6.7)

*) При условии г- -~-) = 2+ (~) т. е. при условии А(0)=0, которое .далее всегда предполагается выполненным.

если s нечетно на полупериоде, т. е. z{t) - симметричная функция и

к ( ) = -i (Vm ) - /5 (Vm-f) .

m=l,2,

(6.8)

если s четно на периоде, т. е. z{t) не обладает симметрией. Для анализа несимметричных автоколебаний в релейных автоматических системах с несимметричной характеристикой релейного элемента и устойчивой линейной частью также введем два годографа

,M=-i4r(v,-)-A(v,-f),

(6.9)

(6.10)

а для анализа несимметричных автоколебаний в релейных автоматических системах с несимметричной характеристикой и нейтральной линейной частью годографы

l()==-i4-(l)-/22(-$-).

В отличие от (6.9), здесь

kp - Уо

- известная величина.

Наконец, для связной релейной автоматической системы удобно ввести семейство частных годографов

s.(-m+%)~iM+%) (6-11)

а, = 0; к, s=l, 2, .... и общие годографы

4(fo)=2/sft(fo). (6.12)

Все приведенные годографы релейных автоматических систем и будут далее использованы для анализа возможных периодических режимов.

Условие отсутствия дополнительных переключений (5.42) - (5.45) не связано с годографами релейной системы, но оно все-

гда' может быть проверено при непосредственном построении формы автоколебаний (см. главу XI). Далее всегда будем предполагать, если не оговорено противное, что условие отсутствия дополнительных переключений выполняется.

С помощью годографов релейной автоматической системы очень удобно качественно и количественно исследовать влияние структуры и параметров линейной части системы и параметров релейного элемента на частоту и форму автоколебаний.

§ 6.2. Годографы релейных систем без зоны нечувствительности

Проверку выполнения условий существования автоколебаний и фактическое определение их частот весьма просто осуществить, используя понятие годографа релейной системы /(со). Для этой цели построим на комплексной плоскости / график годографа релейной системы при возрастании to от О до оо (рис. 6.2). Практические способы построения /(со) будут, описаны далее.

Проведем на этой же плоскости прямую, параллельную действительной оси и отсекающую на мнимой оси отрезок, равный -Ко. Для краткости эту прямую будем называть прямой -ко. Точки пересечения прямой -ко с годографом /((о) релейной системы, расположенные в левой полуплоскости, определят частоту возможных автоколебаний.

Действительно, как следует из рис. 6.2, для этой точки и шо справедливы соотношения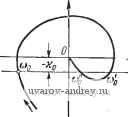

ReJ(ay

Рис. 6.2. К определению частоты автоколебаний. Годограф н прямая -Ко.

Im / (tOo) = - Ко, Re / (tOo) < О,

(6.13)

которые в силу определения (6.2) годографа релейной системы и равенства x(t) =-z{t) соответствуют условиям надлежащего момента переключения и надлежащего направления переключения (5.40). Остальные точки пересечения прямой -ко с /((о), обозначенные через to и to, второму из условий (6.13) не удовлетворяют и, следовательно, они не могут определять частоты возможных автоколебаний.

Если основная задача состоит лишь в определении частоты возможных автоколебаний, то может оказаться удобным использовать действительную и мнимую части годографа релейной автоматической системы порознь (рис. 6.3).

в этом случае на графике 1т/(со) проводится прямая, параллельная оси абсцисс и отсекающая отрезок -хо на оси ординат. Абсциссы точек пересечения этой прямой с кривой 1т/(ш) определяют значения соо, которые будут соответствовать

частотам автоколебаний, если при этих величинах Re/((uo) отрицательна. Так, на рис. 6:3 частота возможных автоколебаний равна ©о- При отрицательном гистерезисе следует прямую -хо заменить прямой -j-Ko.

Если в релейной автоматической системе гистерезис отсутствует, то Хо следует положить равным нулю, и роль соответствующей прямой будет играть ось абсцисс.

Годограф релейной автоматической системы / (со) можно определить по частотной характеристике или по временным характеристикам, или, наконец, по передаточной функции линейной части системы. Рассмотрим все три возможности.

Определение годографа /(ю) по частотной характеристике линейной части системы. Согласно (5.13)

О

Рис. 6.3. Опредетение. частоты автоко-ле::аний по деЯствигельной и мнимой частям годографа 1 (со).

4йр ll7o[(2m- 1)ш]

2т- 1

Sin [(2m - 1) (Of -f е ((2m - I) (o)].

Производная z{t) no / будет равна

i (0 = (0 -- Wo [(2m - 1) (o] cos [(2m - 1) ю/ + 6 ((2m - 1) (o)]. Пользуясь равенством (5.24) при ft(0) = 0 и (5.31), находим

= -со- S 1<о1(2т -1)и]соз((2т -1)со) + А:рШ(0). (6.14)

Отсюда на основании (6.2) получаем

/п\ 4fep Vl{2m- !) ] Im/(a)) = -2(-J =

2m - I

Re / (CO) = - Ш = S t(2 - I) CO] -

. kpw (0)

(6.15) (6.15)

Где

K[(2m- 1)со] = Го[(2т - l)(o]sine((2m - l)(o) f/[(2m - 1) od] = Го [(2m - 1) (oj cos e ((2m

-Deo)/

-мнимая и действительная части частотной характеристики Г[/(2т- 1) ] (см. 2.64).

Таким образом, выражение для годографа релейной си-стем ы принимает вид

/((o) = Re/((o)-f/Im/((o) =

4ko л и;(0)

1Г^-Т -+ / 2m-l 1

(6.17)

При Ky(0) = 0 получаем

F[(2m- 1)ш]

2m- 1

(6.18)

Рассмотрим подробно именно это выражение годографа. Первое слагаемое годографа /(to) (6.18)

4k k

представляет собой частотную характеристику разомкнутой системы, в которой релейный элемент заменен усилителем с коэф-

фициентом усиления

Остальные слагаемые в (6.18) зави-

сят от частот, кратных ш.

Из структуры выражения (6.18) вытекает способ построения годографа / (to) по частотной характеристике линейной части системы W(ja).

Пусть задана частотная характеристика линейной части системы W{j(u) (рис. 6.4). Для вычисления /(ш) при ш = toi отметим на частотной характеристике W{j(o) точки, соответствующие *1астотам toi, Зт, 5(oi, (2m-1)ю1, ... Уменьшим ординаты

этих точек в (2т- 1) раз и проведем к концам уменьшенных таким образом ординат векторы из начала координат (см. рчс. 6.4). Геометрическая сумма всех этих векторов, умноженная

на -- и будет равна значению го-

m/cjl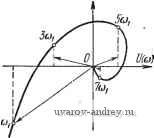

дографа /((о) при ш = toi.

Иногда удобно строить годограф /(ю), используя выражения для его мнимой (6.15) и действительной (6.15) частей (при w{0) =0).

Пусть заданы действительная U (ш) и мнимая К(ю) части частотной характеристики W{j(ii).

На рисунке, где изображено f(cu), строятся кривые L[(2m-1)ю], которые получаются из О (а) простым пересчетом аргумента (рис. 6.5,а). Каждая точка ioi на кривой U (ш) соответствует значению ш для

кривых и[(2т - 1)(й], равному соответственно Сумма

ординат полученного таким образом семейства кривых в каждой

точке (О равна Re /(ш).

Рис. 6.4. Частотная характеристика линейной части.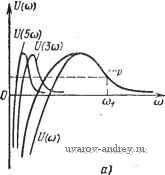

ImJlu)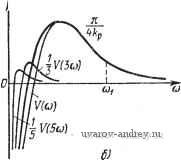

Рис. 6.5. Построение действительной Re / (со) и мнимой Im / (to) частей годографа / (со) по действительной U (со) (а) и мнимой V (со) (б) частям W (/со).

Аналогичным образом на графике, изображающем V((u) (рис. 6.5,6), строятся кривые - 1

строение отличается тем, что ординаты каждой кривой уменьшаются в (2т- 1) раз. Сумма ординат полученного таким об-.-

разом семейства кривых в каждой точке to равна -Im/((u).