того как пересечет этот же порог еще нечетное число раз, достигает порога Ко и проходит его, вызывая очередное переключение релейного элемента (кривая /, рис. 5.8). Этот случай качественно не отличается от случая отсутствия скачка x{f) при

Если же x(t) после скачка изменяет знак, т. е. ~-(.£LW+(-) < О, то x{t) при t = - лишь касается порога

\ Шо / \ ©о / Шо

-Ко, не пересекая его, а далее пересекая этот порог -щ четное число раз (кривая 2, рис. 5.8), либо не пересекая его (кривая 3, рис. 5.8), достигает порога ко, вызывая очередное переключение релейного элемента. В связи с этим в релейной системе возможно существование различных форм и частот автоколебаний. Поскольку при отсутствии скачков в силу- (5.48) условия существования автоколебаний (5.51) и (5.52), (5.52) переходят в (5.40) и (5.41), (5.41), то далее мы и будем использовать именно условия, приведенные в этом параграфе, в которых фи

гурируют левые значения х{t) при - - и t - y-, т. е.

\ ш; \ Шо / \/ (Во /

- О

§ 5.5. О сложных видах автоколебаний

Одним из условий существования симметричных автоколебаний, которые рассматривались в предыдущих параграфах настоящей главы, являлось требование отсутствия дополнительных переключений внутри полупериода их. Выполнение этого условия может быть, как было уже отмечено выше, проверено путем построения формы автоколебаний (см. гл. XI).

В тех случаях, когда это условие не выполняется и, следовательно, внутри полупериода имеются дополнительные переключения, простейшие симметричные автоколебания отсутствуют и можно ожидать наличия более сложных гидов автоколебаний. Последние могут существовать также и наряду с простейшими симметричными автоколебаниями.

Отличие этих более сложных видов автоколебаний состоит в том, что повторение формы их происходит в общем случае через S переключений.

Ограничимся далее, для простоты изложения, рассмотрением релейных систем без зоны нечувствительности. Учет последней, не представляя никаких принципиальных трудностей, приводит к более громоздким выкладкам. Сложный вид автоколебаний в релейной автоматической системе характеризуется наличием переключений внутри интервала, равного половине периода или

периоду. Выходная величина релейного элемента y{t), воздействующая на линейную часть системы, т. е. управляющее воздействие, может иметь вид, показанный на рис. 5.9, а (при s нечетном на полупериоде) и рис. 5.9,6 (при s четном на периоде).

t, и

Рис. 5.9. Управляющее воздействие у (f) при сложной форме авгоколебаннй; а) если s- нечетное на полупериоде, б) если s-четное на периоде.

Если S нечетно на полупериоде, то функция y{t) симметрична относительно оси абсцисс, или, кратко, симметрична, т. е.

(5.53)

где--полупериод.

©О

Если S четно на периоде, то функция (/) не обладает указанной симметрией и в этом случае

yU\=~y{t),

(5.54)

где--период, а юо, как и ранее, обозначает основную ча-

стоту автоколебаний.

Как в первом, так и во втором случае автоколебания будут определены, если можно найти s вещественных величин юо, уь

У2, . . ., ys-I.

Эти величины определяются исходя из условий существова ния сложных видов автоколебаний.

Для того чтобы сформулировать условия существования необходимо предварительно, как и ранее, найти реакцию линейной части системы на указанную сложную последовательность импульсов.

Для этой цели используем способ, в основу которого положена частотная характеристика линейной части системы.

Найдем разложение указанной последовательности импуль- сов в ряд Фурье, применяя общие формулы коэффициентов Фурье (5.3) и (5.5). Полагая в них s вместо S\ (при s нечетном) и сместо S + I (при s четном), получим

для симметричной функции (s - нечетно)

С.-,-т;,(50РЛ).- - -<. (5.56)

ДЛЯ несимметричной функции (s - четно)

Если линейная часть системы нейтральна, т. е. содержит интегрирующее звено, то возможна лишь такая форма y(,t), для которой постоянная составляющая Со равна нулю. Это очевидно из физических соображений. Если же линейная часть системы устойчива, то в общем случае Со может быть отличной от нуля.

Пусть S нечетно (см. рис. 5.9,а). Тогда точками разрыва непрерывности будут:

. я , п , я , п

Скачки в этих точках равны

Dy{U)=-2kp, Dy(U) = 2kp, Dy{t,i) = 2kp, Dy{Q~2kp.

Подставляя эти значения в формулу для коэффициентов Сгт-ь получим

rs-l

У(-1)е-- - * +1

.2m-l-l-2m-M= - - /я (2m - I)

(5.57)

Итак, при s нечетном на полупериоде последовательность импульсов, воздействующих на линейную часть системы, будет определяться выражением

yit)=~f, 1С, ,. [--ф..-.] =

-- 2 1 Cm-i cosf(2m - 1)(0о< -ф2т ,]. (5.58)

Пусть теперь s четно на периоде (рис. 5.9,6). Тогда точками разрыва непрерывности будут - , j

, 2я , 2я , 2п , 2я

i=Y.-. 2 = Y2-. .-i=Y.-i:. 4 = - .;

Скачки в этих точках равны

Dy Hi) = - 2kp, Dy {Q = 2kp, ...,Dy = - 2kp, Dy (Q = 2kp. Подставляя эти значения в формулу (5.3), находим

(5.59)

Таким образом, при s четном на периоде последовательность импульсов, воздействующих на линейную часть системы, будет определяться выражением

= 1 S C,e/> =- + 5]lC,lcos(mof-cp,. (5.60)

Г= -оо Г=1

Формула для8 вычисления,Со приведена в Приложении 2. .Для рассматриваемого случая она имеет вид

Cc=i(-b.- (5.61)

Найдем реакцию линейной части системы, частотная характеристика которой

7(Усо) = Го(©)е/е( ).

При s нечетном

5(0=2 С2 -, 1Го((2т-1)(о„)Х

X COS [(2m - 1) 0)0 - Ф2; -, + G ((2m - I) (5.62)

при s четном

г (О = Wo (0) + 21 С, I Го (/-со) cos [/-Юо - + G (гсоо)]. (5.63)

Можно также выразить z{t) при помощи переходной характеристики линейной части системы. В этом случае число выражений, определяющих z{t) внутри полупериода ~ (при s не-

четном) или периода - (при s четном), будет равно s. Из-за

громоздкости мы не будем выписывать-выражения z{t) в этой форме.

Если учесть, что z(t) удовлетворяет уравнению (5.34) и условию замыкания z{t)=-x{t), то, повторяя буквально рассуждения § 5.3, нетрудно написать условия существования сложной формы автоколебаний (рис. 5.10).

1. Условия надлежащих моментов переключения:

функции y{t) и z{t) симметричны, т. е. s нечетно на полупе-риоде (рис. 5.10, а)

функции у (О и Z (t) несимметричны, т. е. s четно на периоде (рис. 5.10, б).

./ 2я\ / 2я\

(5.64)

2. Условия надлежащих направлений переключений:

s нечетно на полупериоде (рис. 5.10, а) s четно на периоде (рис. 5.10,6)

*-(v.i) = --(v.i)<

/2Я\ /2я\ ~ - = - 2- - >0,

-Ь(.)<о.

СОо

(-1)>0,

-(--.i)-i-(v.-,i)>o, i-(v,..) -i-(,. .)< .

(5.640

Здесь Ко > О при положительном гистерезисе, о < О при отрицательном гистерезисе и хо == О, если гистерезис отсутствует.

Помимо этих условий, должно удовлетворяться условие отсутствия дополнительных переключений. Это условие требует, чтобы x{t) - -z{t) не имело переключений, отличных от указанных выше.

Решение уравнений (5.64), удовлетворяющих условиям (5.64), определяет параметры сложных автоколебаний при s > > 2. Практическое определение этих параметров весьма трудно. При s= 1, vi =1 из (5.64), (5.64) следуют условия существования симметричных автоколебаний (§ 5.4). Аналогично можно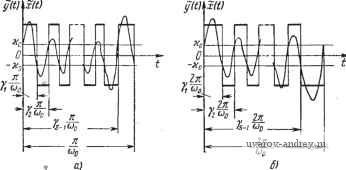

Рис. 5.10. к определению устовий существования автоколебаний стожной формы: а) S-нечетное на полупериоде, б) s-четное на перио.че.

определить условия существования при наличии зоны нечувствительности. Разумеется, при этом число условий существования увеличивается. Поэтому мы не будем эти условия здесь выписывать.

§ 5.6. О несимметричных автоколебаниях

Несимметричные автоколебания могут быть вызваны рядом причин. В релейных автоматических системах с устойчивой линейной частью несимметричные автоколебания возникают при наличии внешнего постоянного воздействия, а в релейных автоматических системах с нейтральной линейной частью- при наличии линейно изменяющегося внешнего воздействия (рис. 5.11).

Несимметричные автоколебания возникают также в тех случаях, когда характеристика релейного элемента не симметрична, например, смещена вдоль оси ординат, как это показано на рис. 5.12, а, б.

Для характеристики релейного элемента, изображенной на рис. 5.12, g, имеет место неравенство

yo>kp. (5.65).

Это означает, что выходная величина релейного элемента не может менять знака. Подобной характеристикой обладают релей -ные элементы вибрационных регуляторов (см. § 2.5),

Для характеристики релейного элемента, изображенной на рис. 5.12,6, имеет место неравенство

0<Уо<йр- (5.66)

Это означает, что выходная величина релейного элемента может изменять знак.

При малых величинах подоб-. ная несимметрия вызывается, например, технологическими или иными погрешностями релейного элемента.

Рассмотрим автоколебания при несимметричной характеристике релейного элемента, предположив вначале, что линейная часть устойчива.

При наличии автоколебаний входная и выходная величины релейного элемента, т. е. управляюш;ее воздействие и управляющий сигнал, будут иметь вид, показанный на рис. 5.13, а, б. Как уже отмечалось в § 3.2, в этом случае управляющее воздействие можно представить в виде суммы постоянного воздействия Уо и последовательности импульсов yi{t), являющихся в установившемся режиме несимметричными.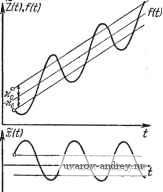

Рис. 5.U. Несимметричные автоколебания при линейном возрастающем воздействии.

о

Рис. 5.12. Несимметричные характеристики релейного элемента: а)- при yk , б) -

при 0<i/g<fep.

Реакция линейной части на постоянную составляющую в установившемся режиме равна

Zo = yJi(oo)=..yoW(0). (5.67)

Эта. величина конечна, поскольку линейная часть системы устойчива.

Реакция системы на несимметричную последовательность импульсов Zi(t) определяется выражением (5.63). Полагая, что

0И

2п

-к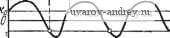

Хо -X,

x(t)

Ж

Рис. 5.13. Управляющий сигнал х (t) и управ.11яющее воздействие В (0: а)-при yk

б)-при 0<j<fep.

S == 2, находим по формуле (5.59) коэффициенты Сг .

или, после элементарных преобразований,

(5.68)

Постоянная составляющая, как это видно из рис. 5.13,6, равна

или

2П

о

--fep(2y,-l).

(5.69)

Подставляя эти значения в (5.63), находим 51(0 = Лр{(2у,-1)\Го(0) +

+ inyynr-cos[ra-ry,n-\rQ(rao)]}. (5:70)

Сумма реакций будет равна

2 (О = 2о + г, it) = [Уо + К (2y, - 1)] 7о (0) +

+ Y.nr cos {ш4 - гу,п + е (гщ)]. (5.71)

Это выражение z(t) справедливо как при выполнении неравенства (5.65), так и (5.66).

Рассмотрим вначале тот случай, когда справедливо неравенство (5.65) (см. рис. 5.12,а).

При постоянном воздействии f входная величина релейного элемента определится соотношением

x{t)f-z{t).

(5.72)

Условие суш,ествования автоколебаний можно записать, исходя непосредственно из рис. 5.13, а или на основании уже ранее найденных условий (5.64), (5.64), когда s - 2, т. е. четно. Эти условия имеют следующий вид:

условия надлежащих моментов переключения:

(5.73)

условия надлежащего направления переключения:

-(f)> -

*-(v,)<o.

(5.730

При этом предполагается, что дополнительные переключения отсутствуют.

Используя (5.67) и (5.72), условиям существования несимметричных автоколебаний можно придать такой вид:

S,(v,--)-/, + .-!/o > (0),

г() .

)>о.

2я ©о

(5.74)

(5.740

Уравнения (5.74) и неравенства (5.74) определяют значения ©о и Yi. характеризующие автоколебания. Величину уь пользуясь терминологией, применяемой в теории вибрационных регуляторов, можно назвать относительным временем замыкания контактов.

Как видно из (5.74), соо и yi зависят существенно от величины fn, определяющей собой настройку (или нагрузку) регулятора.

При отсутствии постоянного внешнего воздействия в условиях существования несимметричных автоколебаний следует положить fn = 0.

Предположим теперь, что линейная часть системы нейтральна, т. е.

< .- = . (6.76)

В этом случае W{0) = <х>. Наличие любой сколь угодно малой постоянной составляющей в управляющем воздействии y[t) приводит к Неограниченному возрастанию выходной величины линейной части z{t). Поэтому постоянная составляющая управляющего воздействия y(t) должна быть равна нулю. Отсюда следует, что

Уо + гр(2у1-1) = 0. (5.76)

Это равенство может быть удовлетворено лишь при выполнении неравенства (5.66), и оно определяет однозначно величину yi,

~ ° le. ТТЛ

р

При этом реакция линейной части системы, обладающей передаточной функцией 11 (р) = qIII) представляет собой z{t) и определяется из (5.71) при учете (5.77) в виде

~z{t) = >] sinу.яг COS[т^ - гу.я + 0 (гщ)]. (5.78)

г=\ .

Интегрируя это выражение по t и учитывая (5.76), находим выражение для z(t):

2 (t) = 2о -f У Sin Y.Jt/- Sin [rtoo t-ry,n+Q (гщ)], (5.79)

где Zo - неизвестная произвольная постоянная. Теперь можно записать условия существования автоколебаний для этогб случая.