Выражения для правых и левых значений z{t) различны для различных форм представлений z{t). Так, если z{t) определяется по частотной характеристике (5.13), то, поскольку (см. Приложение 2)

g(0)(+0) + .(-0)

получаем, учитывая (5.19), при у = 1

Z (+0) = 2 (0) + (0) = f (0) + kph (0).

z (-0) = 2 (0) -1 DS (0) = S (0) - kph (0).

(5.20)

(5.21)

Если же z{t) определяется по переходной характеристике, то из (5.19) получаем при у=1

z{-0) = z{+0)-2kphi0). (5.22)

Введем обозначения для правых и левых значений z{t) в точке ti.

z+{ti)z{ti + 0), z-(ti)

zih-O), I = 2(/,-0). /

(5.23)

Тогда, если z{t) определяется по частотной характеристике, можем записать, учитывая периодичность и (5.21),

= = (0) - kph (0),

= - г- (0) = - г (0) + kph (0).

(5.24)

Если z(t) определяется по переходной характеристике, то с учетом (5.22) имеем

(I ) = -z-(0) = - 2+ (0) -f 2k,h (0).

(5.25)

Случай h{0) ФО может иметь место лишь при / = 0. Действительно, при этом условии согласно (4.25)

(5.26)

dk = h 40)

и, значит.

do = /i(0)= lim Г(р) = - vO.

Обычно этот случай равенства нулю индекса / передаточной функции не встречается в реальных системах. Поэтому далее.

как правило, мы его не будем рассматривать и будем считать / = п -m > О, т. е.

h{0) = 0.

Предположим теперь, что I = п - т = I. Тогда при k - 0 из (4.25) получаем

d==w{0) = h{0)=\im pWip)¥=0.

р->оо

в этом случае z{t) будет непрерывной функцией, причем

.:(-) = -г(0).

Что же касается z{t), то при / = 0, / = -, а значит, и при

t = k-, t = ik-y) (/e = l, 2, 3 ...) функция 2{t) будет испытывать скачки, равные

f 2ki)(0) при у= 1,

от=н+о)-н~о)={ (5.27)

и, значит,

(- - о) = - (-0) + о) = - (+°)-

Аналогично предыдущему получаем, что если z(t) определяется по частотной характеристике, то при у = 1

2 (+0) = ziO) + -Di (0) = I (0) + kpw (0),

i (-0) = f (0) - D2 (0)=i (0) - (0).

(5.28)

A если z{t) определяется по переходной характеристике, то, как следует из (5.27),

(5.29) (5.30)

I (-0) = - г (+0) - 2kpW {0\ z+{h)z{ti + 0), I

Обозначая

1+ (,) = 2(/, + 0), получаем с учетом (5.28)

Ш = - (0) = - (0) + А;рш (0),

если z{t) определяется по частотной характеристике, и с учетом (5.29)

L . . > (5.32)

~ (1) = - ~ = + 2Р^ (0) J

если i(/) определяется по переходной характеристике.

При I - п - т'2, как z{t), так и г(/), непрерывны.

Выше мы рассмотрели поведение разомкнутой релейной системы при симметричном виде внешнего воздействия.

Не представляет труда найти аналогичные выражения для несимметричных и сложных воздействий. Определение выражения z{t) для этих случаев рассматривается в § 5.5.

Если выражения для z{i), представленные в виде ряда гармонических составляющих либо в виде ряда переходных характеристик, тем или иным способом просуммировать, то можно получить выражение для z{t) в замкнутой форме, а не в форме ряда. Для наших ближайших целей в этом нет необходимости, так как мы будем интересоваться лишь дискретными значениями z{t). Определение же z{t) в замкнутой форме будет сделано в гл. XI, посвященной определению и оценке формы периодических режимов (автоколебаний и вынужденных колебаний).

Подчеркнем, что, говоря далее о периодических режимах (автоколебаниях и вынужденных колебаниях), мы всегда будем предполагать простейший их симметричный вид, если не оговорено обратное.

§ 5.3. Условия существования автоколебаний I

Автоколебания в релейных автоматических системах представляют собой периодический режим, поддерживаемый не внешними периодическими силами, а силами, зависящими от состояния системы. Если в релейной автоматической системе имеют место автоколебания, то все величины, характеризующие состояние ее, изменяются периодически с частотой автоколебаний со = СОо.

Обозначим эти периодические изменения xit), y{t), z{t), как и ранее, через x{t), y{t), z{t). Эти величины должны удовлетворять уравнению замкнутой релейной системы

L{XШ = -Wip)L{Ф{Xit); о)}, (5.33)

которое следует из уравнения (2.96), если положить в нем fit) 0.

уравнение (5.33) можно представить в виде уравнения разомкнутой релейной автоматической системы

L {Z т = W{p)L {Ф {X (t); а)}, (5.34)

в котором x(t)-не произвольная периодическая функция, а функция, связанная с z{t) условием замыкания

xit) = -zit). (5.35)

Решение уравнения (5.33) должно удовлетворять условиям переключения, которые определяются видом характеристики релейного элемента Ф(л:;а) и которые в общей форме были использованы при построении переходных процессов в релейных системах (гл. III). Эти условия надлежащего момента и направления переключения в рассматриваемом случае симметричного периодического режима получатся из общих условий для переходных процессов, если положить в них = й - и tk+i =

= (г + у)- <см. табл. 5.1).

(5.36)

При отсутствии зоны нечувствительности и гистерезиса из (3.3) и (3.5) получаем

xik)==0,

-При наличии гистерезиса из (3.12) и (3.14) получаем

(5.37)

причем в этом случае ко > О для положительного гистерезиса и Ко < О для отрицательного гистерезиса.

При наличии зоны нечувствительности из (3.17), (3.17) и (3.19), (3.19) получаем (при Л= 1):

(5.38)

При наличии зоны нечувствительности и гистерезиса из (3.17). (3.1Г) и (3.19), (3.19) имеем

. (ft ) (-!)=> О,

(5.39)

(5.39)

причем О < Я < 1 при положительном гистерезисе, К > 1 при отрицательном гистерезисе, а > О в обоих случаях.

Отметим, что условия (5.37) при ко = О обращаются в условия (5.36), а условия (5.39), (5.39) при Х=\ обращаются в условия (5.38), (5.38).

Для рассматриваемого здесь периодического режима приведенные условия, учитывая периодичность x{t), x{t), естественно упростить, выбрав фиксированное значение ft и, в частности, ft = = О и ft = 1. Полагая в (5.37) ft = 1, получим при наличии гистерезиса

(5.40)

В этом случае ко > О для положительного гистерезиса и ио <С < О для отрицательного гистерезиса.

При наличии зоны нечувствительности и гистерезиса, полагая ft = 1 в (5.39) и ft = О в (5.39), получим

= -Ко

<0.

(5.41)

(5.41)

Здесь О < ?1 < 1 при положительном гистерезисе, \ > 1 при отрицательном гистерезисе, а хо > О - в обоих случаях.

Условия (5.41), (5.4Г) определяют величины юо и у, т. е. частоту автоколебаний и относительную длительность импульсов, воздействующих на линейную часть системы в автоколебательном режиме.

Если найти действительные значения соо и у, удовлетворяющие условиям (5.41), (5.41) (или при у= 1 (5.40)) и подставить их в выражения (5.14) либо (5.16), (5.16) [или при у= 1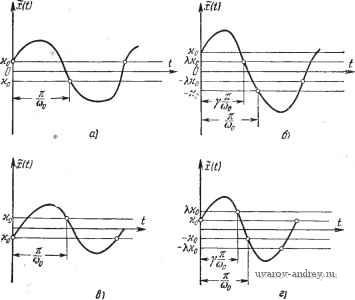

Рис. 5.6. К поясиеиию условий отсутствия дополнительных переключений: а) при отсутствии зоны нечувствительности и положительном гистерезисе, б) при наличии зоны нечувствительности и пололсительном гистерезисе, в) при отсутствии зоны нечувствительности н отрицательном гистерезисе, г) при наличии зоны нечувствительности и отрицательном гистерезисе.

В (5.17)], то МЫ получим выражения, определяющие форму автоколебательного режима. Этот симметричный автоколебательный режим 1зозможен лишь, когда внутри интервала существования импульса 0</<у- и интервала между импульсами

величина x{t) не принимает значений, равных

Шо Шо

пороговым (рис. 5.6), т. е. когда в этих интервалах дополнительные переключения отсутствуют. Считая, что величина x(t) на первом интервале уменьшается, последние условия, называемые условиями отсутствия дополнительных переключений, можно записать аналитически следующим образом;

при отсутствии зоны нечувствительности и положительном -гистерезисе (рис. 5.6, а)

Jc(0>-Xo. 0<<<--, (5.42)

при наличии зоны нечувствительности и положительном гистерезисе (рис. 5.6, б)

х(1)>%щ, 0<t<y~,

(5.43)

©о Шо

при отсутствии зоны нечувствительности и отрицательном гистерезисе (рис. 5.6, е)

x{t)>Ko, 0<t<,, (5.44)

при наличии зоны нечувствительности и отрицательном гистерезисе (рис. 5.6, г)

x{t}>lKo, 0<t<y, (5.45)

Условия надлежащего момента переключения, надлежащего направления переключения и отсутствия дополнительных переключений являются условиями существования симметричных автоколебаний в релейных системах. Этим условиям можно дать наглядную физическую интерпретацию.

Для простоты рассуждений рассмотрим релейную систему без зоны нечувствительности и гистерезиса. Разомкнем эту релейную систему на входе релейного элемента и приложим ко входу разомкнутой системы симметричное периодическое воздействие (в частности, гармоническое воздействие) частоты юо (см. рис. 5.1,6). Тогда в установившемся процессе выходная величина линейной части системы, а значит, и разомкнутой релейной системы z{f) представит собой периодическую функцию z{t), определяемую по формулам, приведенным в § 5.2.

Будем далее предполагать, что эта функция внутри интервала Q<t<- не обращается в нуль.

В общем случае сдвиг фаз между входной x{f) и выходной z{t) величинами отличен от я (рис. 5.7,а). Этот сдвиг фаз является функцией частоты ю входного воздействия x{t) При изменении частоты О) внешнего периодического воздействия будет изменяться и этот сдвиг фаз, и может оказаться, что при некотором значении частоты внешнего воздействия ю = юо сдвиг фаз станет равными (рис. 5.7,6). Тогда, если выход и вход релейной

системы замкнуть так, чтобы г = -х, и одновременно устранить внешнее воздействие, то в ней не произойдет никаких изменений, так как z(t) не зависит от формы входной величины релейного элемента. В системе будут иметь место колебания той же частоты юо, но эти колебания вызываются теперь не внешним воздействием, а силами, зависящими от состояния замкнутой релейной системы, т. е. в системе будут автоколебания.

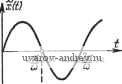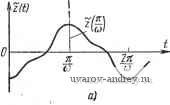
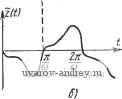Рис. 5.7. Определение условий существования автоколебаний на основе физических соображений: а) сДвиг фаз отличен от п. б) сдвпг фаз равен л.

Как видно ИЗ рис. 5.7,6, сдвиг фаз между x(t) и z(t} будет равен п, когда

]>0.

(5.46)

Если последнее неравенство противоположно, то сдвиг фаз будет равен нулю.

Принимая во внимание соотношение (5.35) между x{t) и z{t) для замкнутой релейной системы, приходим к условиям

которые следуют из (5.40) при о = 0.

Приведенные выше простые физические рассуждения близки к тем рассуждениям, которые обычно применяются при определении границы устойчивости линейных или линеаризованных систем и в результате которых получают уравнения баланса амплитуд и фаз.

Условия (5.46), (5.47) с точки зрения этих рассуждений соответствуют условиям баланса фаз.

Что же касается баланса амплитуд, то в рассматриваемом случае он не играет никакой роли, так как при отсутствии зоны нечувствительности выходная величина разомкнутой релейной системы z(f) не зависит от амплитуды внешнего воздействия.

При наличии зоны нечувствительности изменение амплитуды внешнего воздействия сказывается лишь на сдвиге фаз и относительной длительности импульсов.

Аналогичным образом можно рассмотреть и релейные системы с гистерезисом или с зоной нечувствительности. В случае систем с гистерезисом сдвиг фаз должен отсчитываться от момента переключения x{t), определяемого как момент времени, при котором x{t) проходит через пороговое значение +щ.

Для релейных систем с зоной нечувствительности одновременно с изменением частоты внешнего воздействия нужно изменять его форму (влияющую на относительную длительность -у последовательности импульсов yif)) так, чтобы были выполнены условия баланса фаз, тождественные условиям существования автоколебаний, которые были найдены выше.

§ 5.4. Условия существования автоколебаний И

Найденные в § 5.3 условия существования автоколебаний предполагают, что x(t) непрерывна. Это значит, что в момент переключения = правое и левое значения x{t) равны друг другу:

(5.48)

Если же x{t) при = испытывает скачок, то

В этом случае условия надлежащего направления переключения, приведенные в § 5.3, становятся неопределенными.

Поскольку факт переключения релейного элемента является следствием состояния системы, предшествующего моменту переключения, то условие надлежащего, направления переключения

следуе1 записывать в виде

(5.50)

Таким образом, при наличии скачка jc{t) в моменты переключения, условия существования автоколебаний запишутся в следующем виде:

При наличии гистерезиса

(5.51)

Здесь Ко > О соответствует положительному, а ко < О - отрицательному гистерезису.

При наличии зоны нечувствительности и гистерезиса

Рис. 5.8. Характер измеиеиия х (<) при

наличии скачка х (t) при (=- : x{,t)

дополнительно пересекает порог нечетное число раз (кривая /), четное число раз (кривая 2) либо не пересекает его (кривая 3).

©о/

<0,

(5.52)

(5.520

где О < Л < 1 для положительного гистерезиса, X > I для отрицательного гистерезиса, а ко > 0.

Условия же отсутствия дополнительных переключений

остаются прежними (5.42) - (5.45). Наличие скачка x{t) при t=- вносит некоторые особенности. Здесь возможны два слу-

чая в зависимости от того, не меняет или меняет x{t) после скачка свой знак. Характер изменения x{t) при выполнении условий надлежащего момента и направления переключений изображен на рис. 5.8.

Если x{t) после скачка сохраняет знак, т. е. >

> о, то x{t) при t = - пересекает порог -ко, а далее, после