Характеристика релейного элемента

Процессы на входе и выходе

Фазовый портрет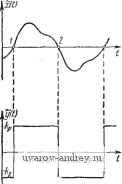

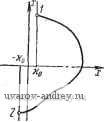Периодическое изменение входной и выходной величин релейных элементов

Характеристика релейного элемента

Процессы на в.ходе н оы.чоте

Фазовый портрет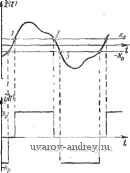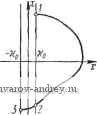

-Xif, -X,

-Ко

о

Важно подчеркнуть, что если различные вхоОные величины проходят пороговые значения в одном и том же направлении в одни и те же моменты времени, то форма их не будет сказываться на выходной величине релейного элемента y{t), а значит, и на выходной величине линейной части системы, z{t).

Как видно из табл. 5.1, наличие зоны нечувствительности приводит к тому, что в некоторые интервалы времени y{t) обращается в нуль, тогда как при отсутствии зоны нечувствительности y{t) проходит через нуль только при изменении знака x{t). В зависимости от знака гистерезиса величина y{t) изменяется с большим или меньшим запаздыванием.

Выходная величина релейного элемента y{t) воздействует на линейную часть системы. Найдем вызываемые при этом вынужденные колебания линейной части z{t). Они представляют собой реакцию линейной части системы на периодическую последовательность импульсов y{t). Эти вынужденные колебания устанавливаются и могут быть наблюдаемы, если линейная часть системы не является неустойчивой*).

Для определения z(t) удобно представить y{t) в виде элементарных слагаемых, реакция линейной части на которые может быть найдена без труда, В соответствии с принципом наложения, реакция линейной части на сложное воздействие равна сумме реакций линейной чйсти на эти элементарные воздействия.

В качестве элементарных воздействий целесообразно выбрать гармоническое воздействие е' и воздействие вида единичного скачка, реакции на которые (см. § 2.2) определяют частотную и переходную характеристики линейной части системы.

Периодическая последовательность импульсов y{t) может быть представлена при помощи ряда Фурье в виде суммы гармонических составляющих Сге^* с кратными частотами га:

Комплексные коэффициенты Фурье С^. ==[ !е~ для функций, состоящих из горизонтальных участков прямых (а именно такой функцией является y{t)), определяются формулой**)

Cr-%Dy{U)e~\ (5.3)

В формуле (5.3) Dy{ti) означает величину скачка функции y(t) в точках разрыва непрерывности U (i = 1, 2, ..., s-f 1).

*) Отметим, что все окончательные результаты справедливы и для того случая, когда линейная часть системы неустойчива. **) Вывод формулы (5.3) см. в Приложении 2.

Величина скачка равна разности значений функции справа y(/j + 0) и слева y(ti - Q) (рис. 5.2), т. е.

Dy{ti)y{U + Q)-y{ti-)- (5.4)

В частном случае, если функция y(t) симметрична, (см. Приложение 2) имеем - Czm = О и

Определив по формулам (5.3), (5.4) комплексные коэффициенты Фурье Сг=\Сг\е~-, ряд Фурье (5.2) можно запи-j сать в виде

Т W=i- S 1с.к'( -4 (5.6)

i>y(ti)

0)

или в вещественной форме

ti t

Рис. 5.2. Скачок функции у U):

(/) = + SI 1 COS {ш1 - ф,). (5.7)

Для симметричной функции y{i) будем иметь

() = Т i !C, -,lef - *-V:-.], (5.8)

ИЛИ в вещественной форме

Р (0= 2 I С2 , Icos[(2m- 1)со/-ф2 , ,]. (5.9)

Таким образом, представление (/) в виде суммы гармонических составляющих сводится к определению комплексных коэффициентов Фурье Сг= Сге~-(т. е. их модулей \Сг\ и фаз фг) и подстановке их в выражения (5.6) -(5.9).

Пусть y{t) имеет вид, изображенный на рис. 5.3, а. Эта функция симметрична и соответствует выходной величине релейного элемента с зоной нечувствительности.

Точками разрыва y(t) являются:

Скачки функции в этих точках равны

По формуле (5.5) находим

или

так как

jn (2m

Замечая, наконец, что

j -/(2m-i)YH 2 sin (2m - I) у -/(2m-l)v

I {2m. - 1)я получаем окончательно:

(2m - I) я

(2;s.n(2/7z-l)Ye

Воспользовавшись выражениями (5.8) или (5.9), находим

~/л 2*Р V 1 /о 1Л я / (2m-l) -(2m-l)Y4l ,с ,

или в явной вещественной форме

4.р - i (2m-l)y г/(0 = - 2-г^-;-cos

2т- 1

(2т -1)со -(2т -1)y . (5.11)

Выражения (5.10), (5.11) определяют выходную величину релейного элемента при наличии зоны нечувствительности (рис. 5.3, а). Для того чтобы найти аналогичное выражение для выходной величины y{t), если зона нечувствительности равна нулю (рис. 5.3,6), достаточно в найденном выражении (5.11) положить y= 1- Тогда, принимая во внимание очевидные тождества

sin(2m-l)4 = (-l) - .

(2m - 1)со/ -(2m -1),у ==(-!) - sin (2m -1) со/.

получим для этого случая:

(5.12)

Заметим, что найденные выражения (5.11), (5.12) остаются справедливыми и в том случае, когда релейный элемент обладает

1ж

п

гистерезисом. Это следует из того, что наличие гистерезиса, как видно из табл. 5.1, приводит лишь к появлению сдвига фаз между входной x{t) и выходной y{t) величинами релейного элемента. Этот сдвиг фаз при положительном гистерезисе больше, чем при отрицательном гистерезисе.

Перейдем теперь к определению выходной величины линейной части системы z(t).

Для определения z{t) нужно найти реакцию линейной части системы на последовательность импульсов y{t). Но эта последовательность представлена в виде суммы простейших гармонических составляющих (5.11) -(5.12). На основании принципа наложения искомая реакция линейной части z{t) будет равна сумме установившихся реакций на каждую гармоническую составляющую.

Таким образом, задача определения поведения разомкнутой релейной автоматической системы сводится к элементарной задаче определения реакции линейной части системы на гармоническое воздействие частоты а^т = гы. А для этого нужно, как показано в § 2.2, амплитуду гармонического воздействия умножить на модуль частотной характеристики системы при частоте, равной (От-, т. е. на Wo(co7-), а к фазе гармонического воздействия прибавить фазу частотной характеристики системы при той же частоте, т. е. е ((От-).

Воспользовавшись этим простым правилом, находим по (5.12) искомую величину г(/) для разомкнутых релейных систем без зоны нечувствительности:

Рис. 5.3. Выходная величина релей ного элемента у {t) при наличии зоны нечув!:твительности (V < 1) (а) и без зоны кечувствигельиости (=1) (б).

2т- 1

sin[(2m- 1)сй/ + е((2т-1)(й)]. (5.13)

Аналогичным образом по (5.11) для разомкнутых релейных систем при наличии зоны нечувствительности получим

Го((2>га- 1)01) 2т - I

sin(2m-l)Y- X

Xcos

(2m -1)(й/ -(2/n -l)Y- + e((2m-1)со) . (5.14)

Полученные выражения позволяют по заданной частотной характеристике линейной части системы определить выходную величину разомкнутой релейной системы z{t) при периодическом воздействии.

Если в выражении (5.14) положить \ - I, то мы придем, очевидно, к выражению (5.13).

Таким образом, z{t) представлено в виде ряда простых гармонических составляющих.

Выходную величину разомкнутой релейной системы z{t) можно также определить по заданной переходной характеристике h{t) линейной части системы.

Заметим, что так как z{t) - периодическая функция, то до-

с\ ± 2я

статочно определить ее поведение в интервале Ur-; в

остальных интервалах она будет периодически повторяться. Для симметричной функции z{t) можно ограничиться интервалом

0/*, в каждом последующем интервале 2(/) будет отличаться лишь знаком. Имея в данном случае в виду симметричные функции 2(0, ограничимся определением z{t) в интервале

0/-, где (О - основная частота.

Значения z(t) в любой точке этого интервала могут быть найдены на основании принципа наложения как сумма реакций линейной части системы на все импульсы, предшествующие этому моменту времени t.

Напомним, что та же идея была положена в основу построения переходных процессов (гл. III).

При рассмотрении вынужденных периодических процессов мы встречаемся с некоторыми особенностями, упрощающими решение этой задачи. Эти особенности состоят в том, что моменты Переключения h полностью определяются частотой периодического воздействия и кратны друг другу и что рассматривается реакция линейной части не на конечное число импульсов, а на бесконечное. Последнее следует из того, что периодическая функция y{t) определяет собой бесконечную последовательность импульсов, определенную в интервале - оо <; / <; оо.

Как указывалось в §§ 2.2 и 3.2, реакция линейной части системы на единичный скачок, приложенный в момент /о,

1(/-/о) =

1 при / > to, О при / < to.

представляет собой переходную характеристику hit - to) при

прямоугольный импульс высоты и длительности Y -. начинающийся в момент to (рис. 5.4,а), описывается выраже-

при

к\ а-to)

to<t<to + y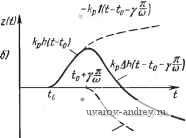

w(-o-y-) =

= p[l(/-g-l(/-/o-Yf) при

Рис. 5.4. К определению реакции линейной части Z (t) иа импульс у (f).

t>to + y.

Реакцию линейной части на такой импульс можно записать в виде:

kph{t-to)

при

to<tto + y

при

kp\h [t~to~y) = kp [h{t-to)-h(t-to-y)

t>to + y

(5.15)

(рис. 5.4,6). Здесь Ayh означает первую разность временной характеристики с шагом у--

Этот результат (5.15) вытекает из принципа наложения. Если импульс представить в виде алгебраической суммы двух скачкообразных функций, смещенных по времени на и отличающихся знаком (рис. 5.4, а -пунктирные кривые) и просуммировать реакции линейной части системы (рис. 5.4, б - пунктирные кривые), то мы придем к искомому результату, который в § 3.2 был получен на основе преобразования Лапласа при рас-, смотрении более общего случая.

Суммируя реакции линейной части системы в интервале 0<-/- на последовательность импульсов, предшествующих

Z(t)

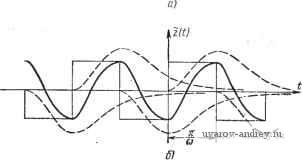Рис. 5.5. К определению г (t) как суммы реакций линейной части на бесконечную последовательность импульсов д (t): а) при V<1. 6) прн у=\.

моменту Времени < = О, т. е. от - оо до О (рис. 5.5.а), находим выходную величину линейной части системы z{t) в виде

Z it) = ftp I л it) + (-If \h [t -b (ft-Y) ~

при 0<<<Y- (5.16)

zit) = kpyi-l),h(t + ik-y)] при Y</<-. (5.16)

fc=0

A/(/ + (ft-Y)-) = ( + )-( + (-Y)~).

Первое выражение (5.16) определяет изменение zit) в интервале существования импульса 0</<-, а второе выражение (5.16) определяет zit) вне интервала существования импульса Y-</<-. На рис. 5.5, а показана жирной линией кривая

z{t), построенная геометрическим сложением реакций линейной части системы. Отдельные составляющие z{t) даны на рис. 5.5, а пунктирными линиями. Если в релейной системе зона нечувствительности отсутствует, что соответствует у= 1 (см. рис. 5.5,6), то тогда z{t) будет определяться одним выражением, которое получится из (5.16) при Y = 1:

г(/) = йр +

а оо

ft=i

при 0<<-.

(5.17)

Жирной линией на рис. 5.5,6 показана кривая z{t). Составляющие z{t) даны пунктирными линиями.

Выражения (5.16), (5.16) и (5.17) определяют искомую величину z{t) через переходную характеристику линейной части системы также в виде ряда.

Отметим, что при у ф 1 периодический процесс, определяемый через переходную характеристику, описывается двумя аналитическими выражениями: (5.16) при О^У и (5.16) при

у-/-. В то же время периодический процесс, определяемый через частотную характеристику, описывается одним аналитическим выражением (5.14).

Если /г(0) - О, то очевидно, что г(0) будет непрерывной функцией, т. е.

Ог(0) = г(+0) -2(-0) = 0. (5.18).

В этом случае

= - г (-0) = г (- + о) = - 2 (+0),

Если же Н{0)Ф0, то при / = 0, t = \-, а значит, и при

t = k-, t = {k - \) функция 2(t) будет испытывать скачки, равные

f 2йр/г(0) при у=1, D2(0) = 2(+0)-2(-0)= /, , (5.19)

I kph (0) при О < у < 1.

В этом случае

М--0) = -2(-0)=(- + 0) = -г(+0),

т. е. в точке разрыва правые и левые значения z{t) не равны' друг другу.