тельное воздействие от производной угла рассогласования (кривая 2), что соответствует последовательной коррекции

к(р)==а1Р+ 1-

Тогда передаточная функция линейной части запишется в виде

W (р)=К. (р) (р) = Тг!р'V р'

где 1 - коэффициент, характеризующий интенсивность действия производной. Теперь

Я(р) = Л 1Р+1) / = n-m = 2, е = --аь , - .) ,

Корень уравнения Р{р) =0 отрицателен, если ai > 0. Для того чтобы релейная следящая система была устойчива в малом, необходимо и достаточно, согласно критерию устойчивости I, чтобы при ai > О выполнялись неравенства (4.30), т. е.

о = - ,>0, d, = -(r -a,)<0,

я- м я ш

откуда следует:

а, > Г„.

Таким образом, система будет устойчива в малом, если коэффициент при производной больше постоянной времени якорной цепи. При этом условии частотная характеристика

W (/со) = К. (/со) W (/со) = , оУЛ 11)+1]/со

получается из Wn(/co) деформацией и принимает вид кривой 5 (см. рис. 4.18). Так как W(/co) расположена в нижней полуплоскости, то и в этом случае условия устойчивости в малом совпадают с условиями устойчивости в целом.

Иной способ стабилизации релейной следящей системы связан с введением внутренней обратной связи, что эквивалентно параллельной коррекции. Пусть

Тогда общая передаточная функция линейной части скорректированной системы запишется в виде

W (р) = К. (р) + IF (р) = + , , ,з^Х., .

Р' Qip) ~ . {Tip - I) (ГяГ„р= + Гир' + р)

Индекс W{p) теперь будет V= 1. Пользуясь критерием устойчивости в малом I, заключаем, что эта система будет устойчива в малом, если нули числителя, т. е. корни уравнения

р (р) = kjjp + ki ту + {k\ + kJ,) p + k,=0

будут иметь отрицательные действительные части, т. е. если будет выполнено неравенство Гурвица

kiTJJt<kJAk, + kJi),

или

ki>K{T,-Ti). (4.131)

Это неравенство всегда может быть удовлетворено выбором и ki и Tl. Неравенство же (4.30)

всегда выполняется при fei > О и Ti > 0. Таким образом, релейная следящая система при выполнении условия (4.131) будет устойчива в малом.

Частотная характеристика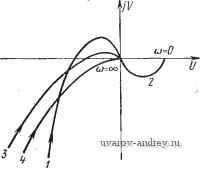

[ТпТи Осо)2 + Г„/а) + 1] /со

Рис. 4.19. Частотная характеристика линейной части (кривая /) и корректирующей цепи (кривая 2). Суммарная частотная характеристика (кривые 3, 4).

может быть построена суммированием частотных характеристик неизменной части системы (рис. 4.19, кривая /) и корректирующей цепи (кривая 2). Она имеет вид, изобра-. женный на рис. 4.19, кривая 3 или 4. Эта частотная характеристика может пересекать действительную Ъсь липгь на высоких частотах. Условие (4.131) обеспечивает отсутствие этого пересечения. Таким образом, устойчивость в малом обеспечивает одновременно и устойчивость в целом.

При наличии запаздывания т в линейной части простой следящей системы, если Тд - О, передаточная функция будет равна

W(p) = U7Jp)=-.-P Полагая р = /со, найдем частотную характеристику

или

Г(/а)) = 15н(У ):

(/СО + 1) /со

fe (ш COS йт + sin йт)

. (cos йт - й sin йт)

где введены относительные величины

Частотные характеристики (при k - I) и различных значениях f приведены на рис. 4.20. Из-за множителя е при любом

т^О частотная характеристика наматывается с ростом ю на начало координат, и поэтому релейная следящая система с идеальным релейным элементом неустойчива в малом. В этом

2уЛыШ1

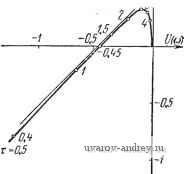Рис. 4.20. Частотные характеристики линей- Рис. 4.21. Модифицированная частотной части прн наличии временного запазды- ная характеристика. Онределеипе ус-вания. тойчнвостн в целом.

случае можно добиться стабилизации релейной системы введением в релейный элемент зоны нечувствительности. Пусть т = = 0,5. Строя модифицированную частотную характеристику (рис. 4.21) и проводя прямую Попова, находим, что при

> 0,55

релейная система будет устойчива в целом.

2. Система автоматической стабилизации курса самолета

Функциональная схема системы автоматической стабилизации курса самолета приведена на рис. 2.12, я.

Как было показано в § 2.5, при введении в управляющий сигнал дополнительно первой и второй производных от курса передаточная функция линейной части системы равна (см. § 2.5, формула (2.109))

- (ИгР^ + aip + I)

Тир' + (Г„М +1) р= + Мр

В этом случае

/(р) = /*Сл( 2Р' + сх,р+1)

и 1укг== п - т = 2.

Корни уравнения Р{р) = О будут иметь отрицательные действительные части, если ai и аг будут поло>*ительными. Вычисляем do и dx по формулам (4.31)

dok.j, 1 = -КГ,.-(Г„М+1)а2].

Система автоматической стабилизации курса самолета будет устойчива в малом, если ai > О, аг > О, и согласно (4.30)

(х,Г,-(Г,М+1)(х2<0.

а, < М-1-4-1 2- 4.132)

Обозначим

1 гр = (м + ~) as.

Тогда условие устойчивости в малом системы примет вид

а, < а, гр.

Величина airp как функция а2 в плоскости (аьаг) представляет собой прямую, проходящую через начало координат (рис. 4.22). Эта прямая делит плоскость на две области. Область / (ниже прямой airp) соответствует устойчивости в малом, а область 2 (выше прямой ai гр) - неустойчивости.

Наклон прямой ai гр зависит от коэффициента М, определяемого типом самолета, и Гм - постоянной времени рулевой машинки. Если Гм - О, т. е. рулевая машинка безинерционна, то наклон прямой airp становится равным бесконечностн (рис. 4.23, g). В этом случае система устойчива в малом при любых значениях

Щ>0, а2>0, М>0. (4.133).

в другом крайнем случае (Гц = сю) наклон становится минимальным и равным airp (рис. 4.23,6). В этом случае область устойчивости в малом 1 минимальна и определяется только величиной М. Чем меньше М, тем меньше эта область. Исследование устойчивости в целом этой системы мы проведем совместно с. исследованием автоколебаний в § 6.7.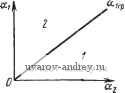

Рис. 4.22. Области устойчивости / и неустойчивости 2 положения равновесия в плоскости параметров (а as).

Рис. 4.23. Области устойчивости / и неустойчивости 2 положения равновесия в плоскости параметров (0, Oj): а)-при Г„=0. б) -при Г„=оо.

3. Система автоматического регулирования температуры.

Функциональная схема системы автоматического регулирования температуры приведена на рис. 2.10. Когда регулируемый объект рассматривается как элемент с распределенными параметрами и постоянная времени измерительного устройства равна нулю, то при наличии жесткой внутренней связи передаточная функция линейной части системы находится по выражению (2.102) (если положить в нем Т„ = О, = оо), т. е.

При этих условиях функциональная схема системы примет вид рис 4.24, а.

Предельная система, которая получается из предыдущей способом, описанным выше, будет иметь вид рис. 4.24, б. Передаточная функция разомкнутой предельной системы равна

ЛР> к Ар) 9

и, следовательно, характеристическое уравнение замкнутой системы будет

p + ft .-V = 0.

Применяя тот или иной критерий устойчивости линейных систем с распределенными параметрами, нетрудно найти условие

устойчивости предельной системы в виде

Р>Р,-р = /г„е- = 0,043/г„.

Интересно отметить, что ргр не зависит от Га *).

р

(4.134)

(2ь

Рис. 4.24. Функциональная схема с11с:емы автоматического регулирования температуры (а| и схема предельной системы (б).

В отличие ОТ рассмотренных выше примеров, воспользуемся здесь выражением импульсной характеристики, которая является оригиналом изображения

Пользуясь таблицей соответствий оригиналов и изображений **), находим, что изображению р/р соответствует оригинал р.

а изображению -е'-оригинал 1-(yV~)

где Ф(йу)= e~ du есть интеграл вероятностей, о

Следовательно, импульсная характеристика будет равна

Воспользуемся теперь критерием устойчивости III, основанным на импульсной характеристике.

*) Устойчивость подобной линейной системы подробно изучалась А. И в а-новым [1], а также Р. Ольденбургом и Г. Сарториусом [1]. К этим работам мы и отсылаем читателя за подробностями.

**) См., например, книгу М. И. Конторовича [1], а также таблицу Приложения 1.

Как следует из выражения w{t),

гг;(0) = f [ft -/г„Ф (оо) + р] = > О,

так как

Ф(оо) = 1.

Следовательно, согласно критерию устойчивости III (по импульсной характеристике) заключаем, что положение равновесия будет устойчивым, если устойчива предельная система, т. е. если выполнено условие (4.134), т. е. если р > 0,043Аи. При р < < 0,043Аи и, в частности, при р = О, т. е. при отсутствии жесткой внутренней связи, релейная система будет неустойчива в малом.

Исследуем теперь устойчивость релейной системы регулирования температуры в целом. При отсутствии жесткой обратной связи р == О передаточная функция линейной части системы имеет вид

Полагая р = /со, получаем частотную характеристику линейной части

W (/ .) = Гн (/ ) = Вводя относительные величины

© = СйГа, k = k -~, с

будем иметь

W (/со) = Гн (/со) = е' =

I со со

Значения действительной f/(co) и мнимой V{a) частей обычной частотной характеристики, а также значения действительной [/ (со) = f/(co) и мнимой Vm(co) == соК(с)) модифицированной частотной характеристики приведены в табл. 4.1.

По данным этой таблицы на рис. 4 25 построены обычная / и модифицированная 2 частотные характеристики линейной части. Как видно из рис. 4.25, в силу того, что Яе Um{0) = = Re f/(0) = - оо и 1/м(со) = со К (со) с ростом со изменяет знак, невозможно провести прямую Попова. Это значит, что введение зоны нечувствительности не гарантирует стабилизацию рассматриваемой релейной системы. Однако стабилизация может быть

достигнута при р > 0. В этом случае частотная характеристика линейной части становится равной

Г(/и) = /г

где р =

Эта частотная характеристика (кривая 3, рис. 4.26) получается суммированием прежней частотной характеристики (кри-

вая /) и частотной характеристики

Р

(кривая 2, рис. 4.26).

JVHJ)

-0,15 -0,1 -D,D5jJM. им

--0,05

Рис. 4.25. Обычная (/) и моди)1щированная (2) частотные характеристики линейной части.

Рис. 4.26. Частотная характеристика линейной части при р^О.

При р > 0,043 суммарная частотная характеристика будет расположена в нижней полуплоскости. Согласно частотному критерию устойчивости (4.116) система будет устойчива в целом при р > 0,043. Таким образом, для этого случая устойчивость в ма-* лом гарантирует и устойчивость в целом.

Глава V

АВТОКОЛЕБАНИЯ В РЕЛЕЙНЫХ АВТОМАТИЧЕСКИХ

СИСТЕМАХ

§ 5.1. Особенности периодических режимов

Одной из характерных особенностей релейных автоматических систем, как, впрочем, и многих других нелинейных систем, является возможность возникновения периодических движений, поддерживающихся не за счет внешних периодических воздействий, а за счет сил, зависящих от состояния системы. Такие периодические движения, следуя А. А. Андронову, называют автоколебаниями. Исследование автоколебаний сводится к установлению существования этого вида движений, к определению частоты и формы, и, наконец, к исследованию их устойчивости.

Автоколебания могут быть физически осуществимы и реально наблюдаемы лишь в том случае, когда они устойчивы, т. е. если малые отклонения от них с течением времени стремятся к нулю.

Точное определение условий существования автоколебаний, их частоты и формы, а также исследование устойчивости автоколебаний в общем случае нелинейных систем представляет исключительно сложную задачу. Однако для релейных систем благодаря специфическим свойствам релейного элемента эта задача может быть решена сравнительно просто.

Специфические свойства релейных автоматических систем, как это уже отмечалось в § 3.1, состоят в следующем. При наличии автоколебаний все величины, характеризующие состояние релейной системы, изменяются периодически. Если же входная величина релейного элемента изменяется периодически, то, как было указано ранее, выходная величина релейного элемента, воздействующая на линейную часть системы, будет представлять собой периодическую последовательность прямоугольных импульсов. Таким образом, в релейных системах форма выходной величины релейного элемента в периодическом режиме предопределена.

Благодаря этому исследование периодических режимов в релейных системах и, в частности, автоколебаний сводится к изучению воздействия периодической последовательности прямоугольных импульсов на линейную часть системы и отысканию их параметров, удовлетворяющих условиям существования периодических режимов.

Прежде чем переходить к установлению условий существования автоколебаний рассмотрим поведение разомкнутой релейной системы при периодическом воздействии. Результаты этого рассмотрения и будут служить основой исследования периодических режимов в замкнутых релейных системах.

§ 5.2. Поведение разомкнутой релейной системы при периодическом воздействии

Разомкнем релейную систему на входе релейного элемента (рис. 5.1,а). Далее, говоря о разомкнутой релейной системе (рис. 5.1,6), мы будем иметь в виду систему, разомкнутую только на входе релейного элемента.

Уравнение такой разомкнутой релейной системы относительно изображений запишется в виде

Z (р) = L {Z it)} = W (р) L {Ф (X it); а)}. (5.1)

В отличие рт уравнения замкнутой релейной системы, которым мы пользовались при построении переходных процессов.

fft) хЮ

Рис. 5.1. Схемя замкнутой (а) и разомкнутой (б) релейной автоматической системы.

здесь на входную величину релейного элемента не наложено никаких условий и она может быть в общем случае произвольной.

Предположим, что входная величина релейного элемента изменяется периодически с частотой (О, т. е. 2л

xiS).

Тогда выходная величина релейного элемента y(t) будет также изменяться периодически. Это периодическое изменение y(i) вызовет вынужденные колебания линейной части системы, т. е. величины z(t) с той же частотой со.

Обозначим эти периодически изменяющиеся величины, в отличие от произвольно изменяющихся величин x(i), y{t), z{t), через x{t), y{t), 2{t). В силу свойств релейного элемента при периодическом изменении входной величины а-(/) = x{t) выходная величина его y{t) ~ y{t) представляет собой периодическую последовательность прямоугольных импульсов постоянной высоты, частоты со и длительности, зависящей от пороговых значений релейного элемента.

В таблице 5.1 приведены для различных релейных элементов примеры периодического изменения входной и выходной величии и соответствующий фазовый портрет.