получаем из (4.96)

S (/(0) = Wi (/(0) + -f + qjaWi (h) + qwo.

Следовательно, условие (4.95) запишется в виде

(4.98)

>0, (4.99)

Re 5 (/со) = Re (1 + qja) 117, (/ш) + qw , .

L Лр J

или, ЧТО эквивалентно.

Re 5 (/(0) = Re {(1 + qja) [j + Г, (/(о)] + } > 0. (4.100)

Но, как следует из (4.37) и (4.97),

К + Wi (6)] e-i< dQ = -\-Wi (/(о) = W (/(О). (4.101)

Поэтому окончательное условие (4.100) запишется в виде

Re 5 (/со) = Re (1 + qja) W (/(о) + > 0. (4.102)

Теперь можно сформулировать частотный критерий устойчивости в целом релейной автоматической системы.

Для того чтобы релейная автоматическая система была устойчива в целом, достаточно, чтобы линейная часть системы была нейтральна или устойчива, а частотная характеристика и параметры релейного элемента удовлетворяли бы условию (4.102), где а = I, <7<0 при положительном гистерезисе, а = Г, <? > О при отрицательном гистерезисе.

Частотному критерию устойчивости в целом релейной автоматической системы можно дать простую геометрическую интерпретацию. Пусть

W (/(о) = f/ ((d) -f ;Т ((d). (4.103)

Тогда неравенство (4.102) можно представить в такой форме:

f/((D) -<?(dI/((d) + ->0.

На плоскости (f/(cD), (d1/((d)) уравнение

и{(а)-д(аУ(а>)-\- = 0

(4.104)

(4.105)

определяет прямую, проходящую через точку-- на оси

абсцисс с наклоном, равным -\-\lq. Эта прямая, называемая

прямой Попова, делит плоскость (U{(u), (oI/(cu)) на две полуплоскости: правую и левую. На рис. 4.9, а, б изображены прямые Попова при 9<0 и Неравенство (4.104) соответствует

точкам области, расположенной справа от этих прямых.

/Х - jcjV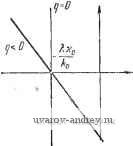

а) 6}

Рис. 4.3. Прямые Попова при (7<0 (а), (?>0 (6).

Введем понятие модифицированной частотной характеристики линейной части релейной автоматической системы

где

И^м(/ )==г/м((о) + /ТЛсо), t/M(cD) = f/((o), УЛ ) = соУ((о).

(4.106)

Как видно из (4.106), вещественная часть модифицированной частотной характеристики совпадает с вещественной частью обычной частотной характеристики (4.103), а мнимая часть отличается от мнимой части обычной частотной характеристики лишь множителем со. Иначе говоря, для получения модифицированной частотной характеристики Um(/(u) достаточно изменить масштаб мнимой части обычной частотной характеристики W {ja) в каждой точке, соответствующей частоте о>, в со раз.

Для устойчивости в целом релейной автоматической системы действительная и мнимая части модифицированной характеристики должны удовлетворять неравенству

f/M(co)-?F (a.) + >0.

(4.107)

Таким образом, мы приходим к окончательной формулировке частотного критерия устойчивости в целом релейной автоматической системы.

Релейная автоматическая система будет устойчива в целом, когда модифицированная частотная характеристика ее линейной части расположена справа от прямой Попова при а = %, 90,

если гистерезис положительный, и при а - 1, qO, если гистерезис отрицательный.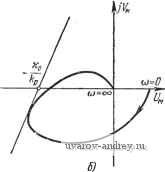

Рис. 4.10. Мопифициропаиные чясготныо характеристики и прямые Попова, соответствующие устойчивой в целом релейной авгоматической системе при наличии зоны нечувствительности и положпгельиого (а) либо отрицательного (б) гистерезиса.

На рис. 4.10 изображены модифицированные частотные характеристики и прямые Попова, соответствующие устойчивости в целом релейной автоматической системы при наличии зоны нечувствительности и гистерезиса.

Для иллюстрации рассмотрим простой числовой пример. Пусть передаточная функция линейной части системы задана в виде

Частотная характеристика системы имеет вид

W {/ ) == 0.5(-2;ш + 1)

По ней, выделяя действительную и{(й) и мнимую V{a) части и умножая мнимую часть

на соответствующее значение о), получаем модифицированную частотную характеристику (рис. 4.11). Проводя прямую Попова, касательную к модифицированной частотной характеристике при а = к, q находим условие устойчивости в целом в виде неравенства

Рис. 4.П. Пример построения модифицированной частотной характеристики и прямой Попова.

< 1,66.

Заметим, что при отсутствии гистерезиса Я- = 1 зона нечувствительности, при которой система устойчива, - минимальна. При наличии положительного гистерезиса О < Я- < 1 необходимая для устойчивости зона нечувствительности увеличивается. Это общая закономерность. Вредное влияние положительного гистерезиса компенсируется зоной нечувствительности.

Критерий устойчивости в целом релейных автоматических систем тесно связан со свойством положительно определенных, или, точнее, неотрицательно определенных функций*).

Рассмотрим функцию 5(р), получаемую заменой аргумента /(О на р в функции 5(/со), стоящей под знаком вещественной части (4.102):

S{p){l+qp)W{p) + - (4.108)

функция S{p) называется вещественной неотрицательной функцией, если:

1) 5(р) вещественна при вещественном р, 2) Re5(p)0 при Re р 0. Поэтому критерий устойчивости в целом релейной автоматической системы можно еще сформулировать следующим образом.

Для того чтобы релейная автоматическая система была устойчива в целом, достаточно, чтобы существовало такое число q О {при а = К) или <? О ( ри а = 1), для которого функция S(p) вещественна и неотрицательна.

Вещественные положительные и неотрицательные функции играют большую роль в теории синтеза электрических цеПей. К сожалению, до настоящего времени отсутствуют простые способы определять по коэффициентам функции 5 (р), принадлежит .ли она к неотрицательным вещественным функциям. Поэтому наиболее удобны сформулированные выше частотные формы критериев устойчивости в целом.

§ 4.7. Частные случаи

Рассмотрим релейные автоматические системы, содержащие релейный элемент без гистерезиса X = 1 с зоной нечувствительности 5<о > О (рис. 4.12, а), либо без зоны нечувствительности 5<о = 0 (рис. 4.12,6). При Х=1 и 5<о = 0 из (4.102) или (4.104) мы получаем критерий устойчивости в большом релейной системы без гистерезиса в виде

Re (1 + qja) W (/(о) + -f > G, (4.109)

f/(cu) -<?a)F((d) + 5->0, (4.110)

*) О них см., например. Воде [1], Н. Балабанпн [1].

где q может быть как положительным, так и отрицательным, т. е. -оо <.q <.°°.

Таким образом, релейная автоматическая система без гистерезиса будет устойчива в целом, если ее линейная часть устойчива или нейтральна и модифицированная частотная характеристика расположена справа от прямой Попова при каком-либо q.

Vl(d)iuV(u)

Рис. 4.12. Характеристики релейных элементов без гистерезиса, с зоной нечувствительности (ИцО, Я=1)-(а) и без зоны нечувствительности (Ио=0) -(б).

Если частотная характеристика линейной части IF (/и) пересекает отрицательную ось и при Re IF (/со) = {/(со) < О представляет собой выпуклую функцию, причем такую, что f/(cu) > > -оо, то, как следует из способа построения модифицированной частотной характеристики 1Fm(/cu), последняя будет также выпуклой. Точка пересечения 1Fm(/cu) и lF(/cu) с отрицательной действительной осью будет одной и той же. Прямые Попова, проходящие через эту точку пересечения, как касательные к 1м(/со) и W(/cu), будут отличаться липаь величиной и, возможно, знаком параметра q (рис. 4.13). Но это обстоятельство, как следует из формулировки критерия устойчивости, не влияет на вывод об устойчивости в целом релейной автоматической системы без гистерезиса. В этих случаях для суждения об устойчивости в целом можно воспользоваться не модифицированной, а обычной частотной характеристикой.

Для релейной автоматической системы с идеальным релейным элементом, т. е. релейным элементом без гистерезиса и зоны .нечувствительности хо = О, из (4.109) получаем

.Re(l+/co)ir(/co)>0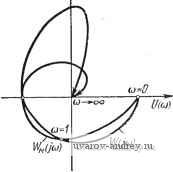

Рис. 4.13. К суждению об устойчивости в целом по обычной частотной характеристике линейной части.

(4.111)

или, при 9 > О,

Re(- + /cuW(/cu)>0.

Аналогично из (4.110) при ко - О получаем

f;(cu)-9mf(cu)>0

или, для 9 > о,

-и (и) -(uF(cu)>0.

(4.112)

(4.113) (4.114)

Для сколь угодно большого q-*oo из (4.112) и (4.14) следует

Re/W(/M)>0 (4.115)

F(cu) = ImlF(/cu)<0. (4.116)

и, значит, со > О,

Неравенства (4.115) и (4.116) определяют различные по форме критерии устойчивости в большом релейной автоматической системы без п^стерезиса и зоны нечувствительности. Как следует

из (4.113), в этом случае прямая Попова проходит через начало координат и формулировка критерия устойчивости в целом релейной автоматической системы без гистерезиса и зоны нечувствительности остается без изменений. Производя в левой части (4.111) замену /со = р, мы приходим к следующей формулировке критерия устойчивости в целом.

Для того чтобы релейная автоматическая система без гистерезиса и зоны нечувствительности была устойчива в целом, достаточно, чтобы (1 +qp)W{p) было веи{ественной неотрицательной функцией.

Более удобна иная формулировка критерия, основанная иа неравенстве (4.116).

Релейная автоматическая система будет устойчива в целом, если ее линейная часть устойчива или нейтральна, и частотная характеристика линейной части расположена в нижней полуплоскости (рис. 4.14).

Из этого критерия устойчивости в целом вытекает критерий устойчивости в малом (см. § 4.4), который требует расположения частотной характеристики линейной части системы в нижней полуплоскости лишь при достаточно высоких частотах. Если

Рис. 4.14. К критерию усточпвосги в целом релейной автоматической cncie-мы без зоны нечувствительности и гистерезиса (и^=0, Я=1).

критерий устойчивости в малом соответствует устойчивости линеаризованной системы при достаточно больших коэффициентах усиления, то критерий устойчивости в целом соответствует устойчивости линеаризованной системы при любых коэффициентах усиления (О < й < с ).

Представим частотную характеристику линейной части в виде

и7(/сй) = И7о{сй)е/ем (4.1.17)

Тогда

Im IF (/со) =10 (со) sine (и), (4.118)

и условие (4.116) будет выполнено при

- я<е(сйХО, (4.119)

т. е. когда фазовая характеристика линейной части системы отрицательна и изменяется от О до л.

Применение условия (4.119) особенно удобно при исследовании устойчивости в целом релейных автоматических систем на основе метода логарифмических фазовых характеристик.

Если IF (/со) представить в виде

Q (/со) Qi И + iQ, (со)

ImlF(/co) = - ) )- )Q- ). (4.121)

Ql (ta) + Qt ( )

Так как знаменатель в (4.121) всегда положителен, то неравенство (4.116) сводится к неравенству

aR (сй2) = Я, (со) Q2 (со) - Яг ( ) Q; (со) > 0. (4.122)

Это неравенство будет выполняться, если полином R{u), где ы = со будет таков, что ЖО) > О и нули его не будут вещественными положительными. Проверка этого может быть осуществлена при помощи теоремы Штурма.

Структура устойчивых релейных автоматических систем без гистерезиса и зоны нечувствительности должна удовлетворять определенным условиям. Они должны совпадать со структурой линеаризованных систем, устойчивых при любом коэффициенте усиления k (О < ft < оо) и, в частности, при достаточно большом коэс})фициенте усиления.

Обозначим через 1ур индекс передаточной функции W{p) непрерывной части системы, т. е. разность степеней ее знаменателя и числителя. Для любой физически реализуемой системы индекс ее передаточной функции представляет собой неотрицательную величину. Необходимым условием устойчивости, как в целом, так и в малом, релейной автоматической системы

является требование, чтобы индекс передаточной функции линейной части не превышал двух.

Обозначим через Wip) передаточную функцию неизменной линейной части. Если индекс

lw >2, (4.123)

то без коррекции невозможно обеспечить упомянутое выше условие.

Рис. 4.15. Релейная автоматическая система с последовательной коррекцией.

При последовательной коррекции (рис. 4.15) передаточная функция скорректированной линейной части определяется как

w{p)=-KApWAp)>

(4.124)

где Кк{р) - передаточная функция корректирующей цепи. Индекс передаточной функции W{p) равен

1 = 4 + 4 (4.125)

где /kj - индекс Кк{р), а так как должно удовлетворять условию

то iKi должно удовлетворять условию

(4.126)

(4.127)

Учитывая (4.123), заключаем, что 1к^ должно быть отрицательным. Это значит, что корректирующая цепь должна вводить чистые производные. Поэтому практически, последовательная коррекция не пригодна для стабилизации релейной автоматической системы.

При параллельной коррекции (рис. 4.16, я) или, что эквивалентно, при охвате релейного элемента обратной связью (рис. 4.16,6), передаточная функция скорректированной линейной части равна

1Г(р) = Кк(р) + (р). (4.128)

Поскольку индекс передаточной функции (4.128) равен

h = mm{k,lw), (4.129)

то всегда можно обеспечить

(4.130)

рде ij = 1 или 2. Выбор параметров корректирующей цепи дает возможность удовлетворить основным требованиям критериев устойчивости в целом или в малом.

Рис. 4.16. Релейная автоматическая система с параллельной коррекцией (а) или эквивалентной коррекцией путем охвата релейного элемента обратной связью (б).

Заметим, что из (4.129) следует, что необходимое условие iw = 1к^~2 не налагает никаких ограничений на передаточную функцию неизменной линейной части Wh{p). Поэтому последняя может содержать элементы с распределенными параметрами, элементы запаздывания.

§ 4.8. Примеры

Применим установленные выше критерии устойчивости в малом и в целом для исследования некоторых конкретных релейных автоматических систем.

1. Следящая система. Функциональная схема следящей си-системы приведена на рис. 2.11. Передаточная функция линейной части системы при пренебрежении постоянной времени якорной цепи Гя (см. § 2.5) имеет вид

Q{p) = Ty + p, Pip) = K.

в этом случае

Следовательно,

Согласно критерию устойчивости в малом I (4.34) заключаем, что положение равновесия релейной автоматической следящей системы устойчиво.

Поскольку частотная характеристика линейной части

полностью расположена в нижней полуплоскости (рис. 4.17), то выполняются требования частотного критерия устойчивости в

Рис 4.17. Частотная характеристика линейной части релейной следящей системы.

Рис. 4.18. Частотная характеристика линейной части для I=n-т=3 (кривая /), цепи последовательной коррекции (кривая 2), суммарная характеристика (кривая 3).

целом (4.116). Таким образом, для идеального релейного элемента условия устойчивости в малом и в целом совпадают.

Если учесть постоянную времени / я, то передаточная функция будет равна (см. § 2.5, формула (2.99))

W7(p)=W (p) =

в этом случае п - /п = 3 и, следовательно, релейная следящая система будет неустойчива^ в малом при любых значениях параметров, отличных от нуля.

Частотная характеристика, определяемая выражением

имеет вид, качественно изображенный на рис. 4.18 (кривая /). Для стабилизации релейной следящей систе;иы введем дополни-