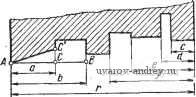Рис. 62. Пример вхождения размера в н6-ско.пы(о массивов

С адресом а, куда засылаются признаки п' и п, конкретное содержание которых ясно из схемы рис. 59. На входе 02П01 формируется содержание счетчика J выделенных массивов по классам. В зависимости от J формируются признаки п' и п ячейки а. Так, при J = 1 происходит выбор массивов концентрических дуг или окружностей; при J = 2 и J = 3 - массивов с меткой К, отличающихся особенностями, показанными на рис. 60 и 62; при Jm =4 - массивов с меткой К, снабженных при кодировании меткой базы (см. рис. 61). Оставшиеся размеры обслуживаются при Jm > 4 специальной подпрограммой 02П01п/п01, которая является выходным фрагментом программы 02П01.

Основным процессом программы является обзор кодов исходного массива размеров, входящих в кодированный размерный граф. Первый по счету выбранный код по каждому из признаков становится заглавным в соответствующем массиве. Каждый выбранный код снабжается меткой i, показывающей, что код использован и в дальнейшем пропускается (исключая переборы при i = 3, где один и тот же код, выбранный при = 2 и при J = 3, может быть пригоден при реализации ситуации, показанной на рис. 62, см. размер г). В таком случае метка использования помещается в другой разряд ячейки и обозначается i, и повторный перебор при J = 3 производится с учетом i. В заключительном фрагменте формируется счетчик кодов данного массива. Кроме того, J о своим, содержанием показывает очередность обработки каждого массива J = / Он имеется у каждого массива, исключая цепочки и одиночные размеры. Подпрограмма 02П01п/п01 по логике аналогична 02П01 и отличается от последней содержанием признаков. При машинном программировании вполне возможно оформление подпрограммы как цикла 02П01.

Алгоритм стандартных подпрограмм комплекса размещения и нанесения размеров на чертеже

Часть стандартных подпрограмм, применяемых в комплексе, находит ограниченное применение только в рамках комплекса. Такие подпрограммы имеют в обозначении символ СТ. Подпрограммы общего назначения имеют символ СТО и ниже не описываются, так как они известны.

Алгоритм подпрограммы 02п/п01СТ определения размеров прямоугольника, вмещающего размерную надпись. Длина L размерной надписи может колебаться в достаточно широких пределах. Это происходит из-за того, что наряду с размерным числом, которое трудно ограничить каким-либо определенным количеством цифр, в размерную надпись могут включаться различные семан-

тические и разделительные символы, а также целые слова. К таким символам относятся, например, R; 0; □ и т. п. Разделительными являются различные индексы, запятые и т. д.

Программа является стандартной, так как применяется для любого размера. Константами служат параметры строки стандартного шрифта (в наших экспериментах был принят шрифт 3,5 по ГОСТ 2.304-68). Логика программы не зависит от констант, поэтому ее можно отладить на любой размер шрифта. Высоту размерного прямоугольника обозначим S, а длину L. Высота постоянна и выбирается в зависимости от размера шрифта. В случае размера 3,5 высота S = 7. Длина L равна длине размерной надписи L с буферными промежутками, равными 0,5 мм каждый и расположенными, как показано на рис. 63. Таким образом.

{начало ) г- ч*

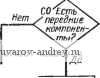Подсчет длины

передней компоненты

,-ЕО-

Подсчет длины размерного числа

r-FO

a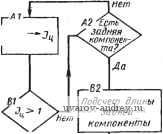

Буферный прометуток Us

Рис. 63. Схема алгоритма подсчета длины размерного прямоугольника: i = ц; 1 = 6 - буква; £ = I, - символ; i = пр - промежуток; ft - число элементов; - ячейка, где накапливается i; aj - адрес ячейки, соответствующей элементу размерного графе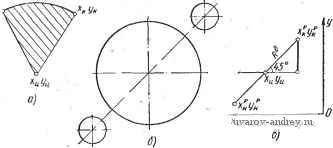

Рис. 64. Области размещения размеров, связанных с окружностью: а - односвязная; б - неодносвязная; в - схема подсчета параметров размерной линии^

L = Lh + 1 ММ. Если на чертеже имеется несколько однородных элементов, то, как известно, размер ставится у одного из них и показывается число таких элементов. Появляются надписи типа: 3 отв. 0 10 й ,т. п. Могут быть дополнения о конструктивных элементах отверстия, например, 0 3,5; h2 X 90°. Таким образом, размерная надпись состоит из размерного числа, которое может быть дополнено двумя компонентами, располагаемыми перед размерным числом и после него.

Схема алгоритма 02п/п01СТ показана на рис. 63. На правом поле сделаны необходимые пояснения примененных обозначений.

Алгоритм стандартной подпрограммы 02п/п02СТ определения параметров размерной сети/, связанных с окружностью. Подпрограмма обеспечивает вычисление координат х1ун начальной и х^к конечной точек размерной линии. Под начальной точкой у размерной линии, имеющей один стрелочный конец, понимается именно этот конец. В случае проставления диаметра окружности размерная линия направляется обычно под углом 45° к горизонтальным линиям изображения. Начальной точкой в таких случаях условно принимается левый нижний стрелочный конец. На входе в подпрограмму выясняется, односвязна ли область размещения размера (т. е. отсутствует окружность или дуга, вложенные во внутреннюю область, ограниченную окружностью либо дугой, размер которых наносится), такая область заштрихована на рис. 64, а. Если область неодносвязна, то 02п/п02СТ не работоспособна, и управление передается на подпрограмму выноса размерного числа с помощью полки. Здесь выполняется проверка: полная ли окружность обслуживается. Если да, то проверяется, нет ли Б чертеже линии, проходящей через центр обслуживаемой окружности под углом 45° (пример приведен на рис. 64, б). Если такая линия ХцУц имеется, то пробуется направление под углом 135 . В случае занятости и этого направления угол наклона размерной линии изменяется на 5° в сторону увеличения угла 45°

либо уменьшения угла на .135 . Если обслуживается дуга окружности, то вычисляются координаты x?pi/?p средины обслуживаемой дуги. Затем проводятся проверки, аналогичные случаю полной окружности и операции по определению параметров размерной линии.

На рис. 64, в изображена схема подсчета параметров размерной линии. Они могут быть подсчитаны по формулам

x:~Xo, - R -у=-;

<: = х, + /? -±.;

Различные комбинации знаков в этих формулах позволяют охватить случаи наклона размерной линии как под углом 45°, так и 135° (так, для последнего случая в формуле (А) будут оба плюса - пусть это будет случай А, а в формуле (Б) - оба минуса - обозначим этот случай Б). При изменении системы отнесения Оху с правой на левую, например, меняются знаки в-формулах, куда входят абсциссы. При перемещениях размерной линии на 5° вычисляются приращения координат точек размерной линии, которые являются функциями от радиуса дуги. Различные случаи расположения средины дуги дают различные случаи присвоения значений hx и Ку, которые затем используются для вычисления параметров размерной линии. Схема алгоритма 02п/п02СТ представлена на рис. 65. Для случая полной окружности формула (А) трансформируется в формулу, обозначенную на диаграмме символом С, в которой сомножителем .при RJ будет величина sin 50°.

Алгоритм стандартной подпрограммы 02п/пОЗСТ размещения размерной надписи вдоль размерной линии. Сущность подпрограммы заключается в вычислении величин Lp (в случае дуги) и Lp (в случае линейного размера), выражающих длину размерной линии, на которой может размещаться размерный прямоугольник Б данной ситуации. Вычисленные величины сравниваются с реальной длиной L размерного прямоугольника. Если вычисленная величина больше либо равна L, то вырабатывается сигнал размещения размерной надписи вдоль размерной линии. В этом случае управление получает программа 02п/п05СТ вычерчивания размерной сети. В случаях, когда вычисленная величина меньше L, управление получает программа 02п/п04СТ выноса размера за пределы размерной сети с помощью полки. Напомним, что величина L вычислена подпрограммой 02п/п01СТ. На входе программы

I\Q-

\рачало)

Пет

,-А1-

Вычисление параметров размерной линий т формуле (А)

Область односвязна

Нет

Полная о крут- ность? , HemPD

Есть ли , центровая под 45°

Есть ли центровая под Z73S°? г-ГО

Вычисление параметров размерной линии по(0

TFP-

Вычисление параметров размерной линии по формуле (Б)

Г-С1 -

Вычисление коор-винат средней точки дуги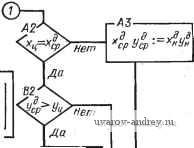

Присвоение метки выноса размера напалку

г-GO

Обращение к алгоритму оптимизации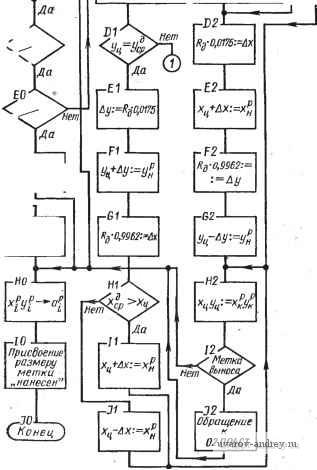

Рис. 65. Схема алгоритма 02п/п02СТ размещения размеров окружности

02п/пОЗСТ линейные размеры отделяются от размеров радиусов либо диаметров. В случае линейного размера длина Lp вычисляется по координатам начальной и конечной точек xyl; xlyl. по известной формуле. Если размер не линейный, то выделяются полные окружности, и Lp вычисляется с использованием ранее высказанных соображений. Высота размерного прямоугольника принимается при этом равной 7 мм, а возможная для размещения длина

{Начало J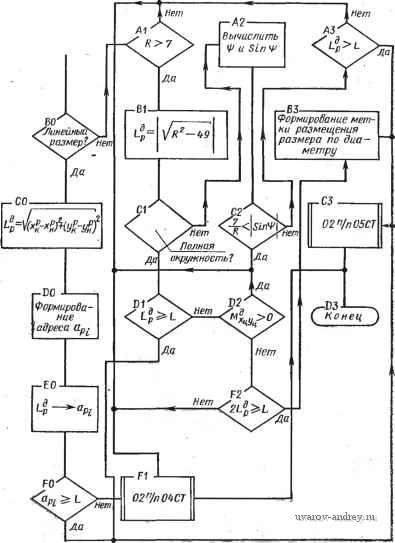

рис. 66. Схема алгоритма 02п/пОЗСТ размещения размера вдоль размерной линии

Mem Nil

{на чало)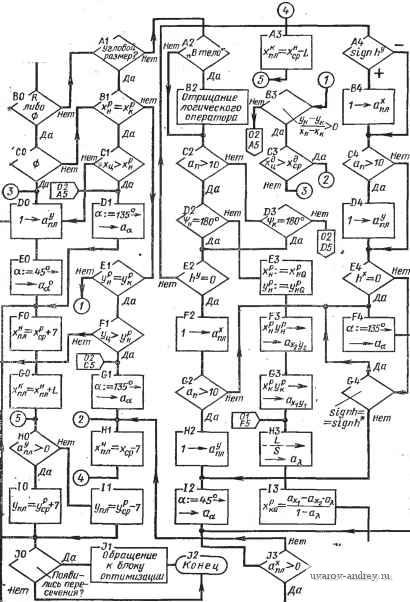

Рис. 67. Схема алгоритма 02п/п04СТ вынесения размерной надписи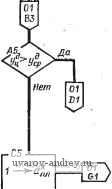

Лист № I

Схема выноса размера

FSJ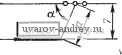

Vr - 49 где r

вычисляется no формуле Lp = окружности. Если обслуживается дуга, то предварительно вычисляется синус половины центрального угла дуги sin яр.

Подпрограммой отражен тот факт, что в окружности возможно размещение размерной надписи не только по радиусу, но и по диаметру (в последнем случае Lp удваивается). Исключаются при этом окружности, входящие в массив концентрических (с меткой Мху^). Ввиду особенностей, возникающих в последних массивах, размещение в них происходит только по радиусу. Логика алгоритма может быть прослежена по схеме алгоритма 02п/пОЗСТ (рис. 66).

Алгоритм стандартной подпрограммы 02п/п04СТ вынесения размерной надписи. Подпрограмма обслуживает те случаи, в которых размерная линия не подходит для размещения вдоль нее размерной надписи. В качестве стандартных выбраны две основные схемы выноса размерной надписи (рис. 67, лист № 2). Схема 02п/п04СТ показана на рис. 67. Входной фрагмент классифици-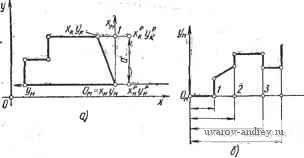

Рис. 68. Типовые-схемы нанесения размеров

рует размеры по некоторым признакам.- Выделяются размеры радиусов, диаметров, а также угловые размеры. В линейном размере различаются случаи введения размера в тело проекции и все остальные случаи. В случае введения линейного размера в тело (это решение принимается до обращения к 02п/п04СТ соответствующей программы), логические операторы обсуждаемой подпрограммы отрицаются (т. е. альтернативы Да и Нет меняются местами). Результаты выводятся во всех случаях в виде параметров выносных элементов, дополняющих параметры размерной и выносных линий, вычисленные программой-потребителем. В схеме а результатами являются:

л^д /?д - координаты, определяющие начальную и конечную точки

продолжения размерной линии, i = н; к; в схеме б:

ХплУпп координаты, определяющие начальную и конечную точки полки, i =н; к; а - выводится только для справок. Алгоритмы стандартных программ 02п/п06СТ вычерчивания размерной сети и 02п/п05СТ заполнения размерного прямоугольника. Эти стандартные подпрограммы получают управление в тех случаях, когда параметры выносных и размерных линий вычислены (02п/п05СТ) и необходимо вычертить эти линии; либо когда надо выполнить размерную надпись, если определено положение размерной линии (02п/п0бСТ). Подпрограммы находятся в зависимости от конструкции чертящего устройства и поэтому не при- водятся.

Алгоритм стандартной программы 02п/п07СТ. Подпрограмма обслуживает те случаи, когда измеряемая протяженность не изображена на чертеже в виде явного отрезка (например, размер а на рис. 68, а). При нанесении размеров, отсчитываемых от одной базы, необходимо задаваться некоторой вспомогательной системой координат О^ХыУ^, от оси которой можно будет начать отсчет параметров выносных линий каждого размера, входящего в данный массив /( (рис. 68, б). За расчетные точки принимаются конечные точки измеряемой фигуры. При вычерчивании выносных

[начало)

ВО-1база?

- СО

Нет

.Нет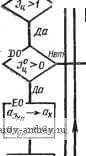

Восстановление адреса засылки

Нет

г-Ю-1-

Г.Э01-

Ог-Ц7гк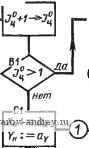

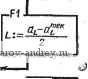ХиУ„-*а^ау

Рис. 69. Схема алгоритма 02п/п07ст размещения размера протяженности, не изображенной на чертеже в виде явного отрезка:

Уд - счетчнк циклов в 02п/п07СТ; ~ счетчик

циклов в 02П03Т00; а = = 1 - метка углового размера

Расчетные схемы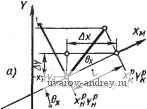

линий эти точки используются как действительные (т. е. входящие в контур изображения) точки во всех алгоритмах комплекса, за исключением 02п/п05СТ. На рис. 69 приведены примеры, отображающие типичные ситуации. Здесь точки 7,-2, 3, 4 - расчетные. Расчетными величинами являются J (xit/i); J = 1, 2, 3, i = = н, к. При этом

Ay = L sin е^; Ах = L cos 6; (В)

1х^ = х„ + Дх,-;1/ = + Д^/,-. (Г)