начальной точке измеряемого отрезка. Наиболее сложными здесь являются два случая: 1) я]; >> 180°; 2) < 180°. Рассмотрим ситуации, возникающие в случае 1.

1. Размер С А нанесен.

2. Размер СА не нанесен.

Исследуем ситуацию 1. Здесь могут быть случаи: 1а) С А внесен внутрь контура; 16) С А вынесен из контура. В случае 1а размер АВ должен быть вынесен от контура (в дальнейшем будем называть этот вынос от тела , а при вводе размера внутрь проекции - в тело ), при таком выносе в размерной сети пересечений вновь не образуется, и обеспечивается возможность размещения размера BD без пересечений с предьщущим размером, внесенным в тело. Если же имеется случай 16, то необходимо включить в рассмотрение я];,. При этом возможно следующее:

а) я]; = 90°, в этом случае отрезок BD либо его продолжение могут быть использованы в качестве одной из выносных линий для выноса размера АВ. При наличии свободного места в теле лучше ввести размер АВ в тело, так как при этом остается более свободный выбор для размещения последующих размеров. Если же свободного места^ в теле нет, то размер АВ выносится от тела. При этом предусматривается возможное пересечение двух размерных линий в дальнейшем;

б) TlJj. = 270°, по аналогичным с предьщущим случаем причинам размер АВ следует вынести от тела;

в) ijj 4= 270°, но я]; >> 180° - следует также вынос АВ от тела -, при этом < 270°;

г) я15 ф 90°, но я]; < 180° либо я]; < 270° - размер АВ следует ввести в тело, так как при этом возникает хорошая ситуация для размещения последующих размеров.

Рассмотрим теперь исходную ситуацию 2, когда размер С А не нанесен на чертеже. Для размера АВ существенны следующие случаи: 2а) я!; = я!;; 26) я1; =f я!;.

Пусть возник случай 2а. Тогда возможно следующее:

а) я15н = я}: < 90°, т. е. перед нами углубление в контуре проекции (рис. 53). Наиболее предпочтителен здесь ввод размера в тело, так как в этом случае меньше вероятность того, что мы повредим смежным размерам;

б) ifi) =Фк 270°, т.е. имеется выступ в контуре. В этом случае предпочтительным является вынос размера от тела, так как тело выступа может понадобиться для ввода в него других размеров, а вынос не приводит к пересечениям в размерной сети;

в) 90° < я15н = я]; < 180° - сводится к случаю а;

г) 180° < я]5 = я]; < 270° - сводится к случаю б. Обобщая последние случаи можно сказать, что ситуации типа а

размещения размеров разделяются в зависимости от того, какая особенность имеется в контуре: выступ либо выемка.

Пусть теперь возник случай 26, т. е. я15 ф я];. Прежде всего проверим, не равен ли один из углов 90° либо 270°, если равен.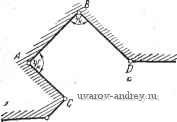

Рис. 53. Случай углубления в контуре проекции

Рис. 54. Ситуация, возникающая при размещении линейного размера

ТО МОЖНО применить ранее рассмотренные случаи а и б ситуации 1. В случае, когда ни один из углов не равен 90° либо 270°, выпол* няется проверка на наличие выемки или выступа (как было показано выше). В результате может быть применена тактика а либо б ситуации 2.

Может возникнуть ситуация, показанная на рис. 54. Она характеризуется тем, что я]; и гр могут быть больше или меньше 180°. Проведем проверки кр > 270° и я]; < 90°. Если эти неравенства не выполняются, то проверяется наличие свободного места во внутренней области проекции (в теле), и если оно имеется, то размерная линия вносится в тело, в противном случае размер выносится от тела. Если неравенство > 270° выполнено, а неравенство < 90° не выполнено, то проверяется \\) > 270°. При выполнении этого неравенства размерная линия выносится от тела. Наконец, если > 270° и < 90°, т. е. выполняются оба исходных неравенства, то размерная линия вносится в тело. Может случиться, что в теле нет свободного места, тогда приходится мириться с пересечением размерной и контурной линий либо идти на изменение угла наклона выносных линий по отношению к измеряемому отрезку, делая его меньше i.

Напомним, что все сказанное применяется пока для случая 1, т. е. когда я]; >> 180°. Рассмотрим теперь случай 2, когда < 180°.

Здесь также возникают две ситуации:

1. Предыдущий размер нанесен.

2. Предьщущий размер не нанесен.

Для ситуации 1 возникают случаи: 1а) размер СЛ внесен в тело и 16) размер СА вынесен от тела (аналогично рассмотренным ситуациям случая 1. В случае 1а размещаемый размер выносится от тела, в случае 16 вносится в тело.

В ситуации 2 измеряется г}: и перебираются альтернативы, изложенные выше для случая 1.

В заключение упомянем о случае 3, когда ilJ, = 180°. Это наиболее простая ситуация, так как размещаемый и последующий размеры не мешают друг другу. .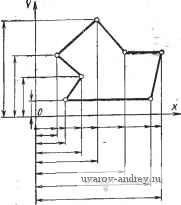

Рис. 55. Внешняя параметризация контура

Остановимся на двух способах формирования размерной сети при нанесении размеров: 1) цепочкой, когда конец предыдущего и начало последующего размеров совпадают; 2) от одного базового ограничения (в дальнейшем этот способ называется координатным).

Как известно, отмеченные способы реализуют различные ситуации, связанные с выбором баз. Базы выбирают в процессе увязки функциональных свойств конструкции с геометрическими ее параметрами либо со свойствами обрабатывающего оборудова-Н.ИЯ, с помощью которого будет получена данная форма. Таким образом, выбор способа нанесения размеров здесь не включается нами в автоматический процесс. Он должен быть задан с помощью исходного размерного графа.

Обозначим метку координатного метода М^., а цепочки М^. Пусть имеется метка М^., рассмотрим случай ipj = 180°. Если предыдущий размер имеется, то проверяется наличие свободного места в теле с учетом продления выносной линии, а также с учетом размещения размерной надписи в данной зоне (учета,). При наличии места размер вносится в тело, в противном случае размерная линия выносится от тела. В случае, когда предыдущий размер не нанесен (если начали с размера АВ), то сначала наносится он и все сводится к только что рассмотренной ситуации.

Весьма распространены случаи, когда в кОнтуре имеется множество элементов, протяженность которых измеряется в направлениях, параллельных координатным осям базовой системы координат. Наиболее общая форма такого случая (рис. 55) сводится к внешней параметризации какого-нибудь контура. Если оси координат совпадают с элементами измеряемого контура, то это.будет внутренняя параметризация. На рис. 55 контур определяется координатами своих вершин. Число размерных линий, параллельных осям координат, равно числу вершин контура, имеющих отличающиеся друг от друга соответствующие координаты. При нанесении размеров с выносом каждой размерной линии выносную линию приходится продлевать на заранее обусловленную постоянную величину (например, 10 мм). Таким образом, /С-й из несовпадающих по величине размеров будет вынесен на расстояние ЮК от соответствующей оси координат. Если же измерить величину выноса размера от концов измеряемого отрезка, то, обозначив эту величину через Н, получим Н = ЮК + Т, где Т - численная величина координаты точки отрезка, где начинается

выиоснай линия, измеренная вдоль этой линии. Приведенная формула позволяет оценить величину зоны размерной информации в этом случае. Если же свободное место на чертеже меньше требуемой зоны, то можно изменить формат листа либо применить одну, продолжающуюся в сторону нарастания размера, размерную линию (на рис. 55 этой линией является размерная линия, наиболее близкая к Ох). В последнем случае размерная надпись наносится у конца каждой выносной линии с учетом признака а (выносная линия при этом играет роль размерной): Следует отметить, что изложенные правила пригодны и в случае нанесения угловых размеров.

Размещение размеров окружностей и концентрических дуг

При нанесении размеров, связанных с окружностью, в общем случае необходимо нанести три размера: координаты центра и радиус либо диаметр окружности. Координаты центра включаются в общий массив точек контура и размеры их наносятся как линейные. Для нанесения размера радиуса либо диаметра проводится расчет места внутри области, ограниченной окружностью для размещения размерного прямоугольника. Максимальная высота размещаемого в упомянутой области прямоугольника при длине размерной надписи L зависит от радиуса окружности R:

Если вычисленная / < S, то размерную надпись необходимо выносить за пределы области, ограниченной окружностью. В противном случае размерную надпись размещают в области. При этом размерная линия наклоняется под углом 45° к осям координат.

При проставлении размеров концентрических дуг применяется тактика, аналогичная той, которая используется при нанесении линейных размеров. Зоны выделяются областями, на которые поле чертежа делится двумя взаимно перпендикулярными диаметрами образмериваемых окружностей. Если имеется множество неконцентрических окружностей (более трех), то может быть применен табличный метод указания размеров, разрешенный ГОСТ и весьма удобный для реализации на ЭЦВМ.

Нанесение размеров в случаях неодносвязного контура

Неодносвязный контур проекции может быть разбит на связные компоненты, каждая из которых в конечном счете односвязна. Параметры такой компоненты делятся на параметры формы и положения. Последние связывают данную компоненту с какими-либо элементами проекции либо с базовой системой координат. Таким образом, параметрами положения являются размеры, определи-

B(Xbytf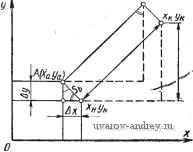

Рис. S6. Определение наПра ВлеНИя выноса линейного размера

ющие положение местной системы координат, Б которой реализуются параметры формы обслуживаемой компоненты. В процессе нанесения размеров в случае неодносвязного контура основным циклом является процесс нанесения размеров в одно-связном контуре. При этом сначала обслуживаются все внутренние контуры, затем наносятся размеры, реализующие параметры их положения. В последнюю очередь наносятся размеры объемлющего контура по правилам

ОДНОСБЯЗНОГО.

Определение положения размерных и выносных линий при выбранном направлении выноса

Пусть (рис. 56) имеются две точки А я В контура проекции. Их координаты xltJa, ХьУь- Необходимо определить положение выносных и размерных линий размера АВ, если направление выноса выбрано. Из элементарных геометрических соображений заключаем, что координаты начальной точки размерной линии, которые определяют и основную, будут:

х„ = х„ ± Дх; у^ = Уа± Ау

(аналогично могут быть найдены xyj. Знак в формулах зависит от направления выноса. Величины Ах и Ау зависят от величины выноса S, определяемой из формулы Ах -\- Ау = S; с другой стороны,

I Ук - Ун I

откуда .

Ах = (IУ к-Ун I)

\Хк - х„\

Обозначая Цу - Уп /{х^ - х„\) через k, получим Ах = Ayk. Тогда kAy Ау2 или Ау = S4{k + I).

Подставляя значение k и находя арифметическое значение корня, получим формулы

Дх = 5

У к -Ун % - %

{ Ук~Уи Y \ Хк - X /

-f 1

/ Ук-Ун V \ Хк. - х„ J

-f 1

{/к - {/н

Хц- Хц

представляет

В этих формулах выражение

собой тангенс угла наклона отрезка АВ, а следовательно, и размерной линии по отношению к оси Ох. Это выражение можно

заменить на равное ему

Тогда

ХЬ - Ха

УЬ - Уа ХЬ - Уа

\ХЬ - Ха )

\хь - Ха)

3. ОСНОВНЫЕ АЛГОРИТМЫ РАЗМЕЩЕНИЯ И НАНЕСЕНИЯ РАЗМЕРОВ НА ЧЕРТЕЖЕ

Рассмотрим алгоритмы, реализующие формальные модели предьвдущёго параграфа.

В качестве исходной для нанесения размеров на чертеже берется информация о координатах точек чертежа, между которыми измеряется расстояние. Точки упорядочиваются таким образом, что при движении от начальной к конечной точке измеряемой протяженности контур, в который она входит, на проекции остается слева. Окружность задается координатами центра и радиусом. Дуга окружности, кроме того, - координатами начальной и конечной точек. Угол задается координатами вершины, величиной, координатами конструктивных точек контура, лежащих на сторонах угла. Таким образом, размеры, которые необходимо нанести на чертеже, заданы, и алгоритмами реализуются только процессы их размещения на поле чертежа и нанесения по правилам ГОСТ.

Особенностью излагаемых алгоритмов является то обстоятельство, что часть из них реализует процессы, применяемые Б различных типовых ситуациях. Такие алгоритмы организованы Б виде стандартных подпрограмм либо операторов. В свою очередь, структура подпрограмм также оказалась сложной и внутри них понадобилось выделять стандартные процедуры, которые организованы Б виде тактических и исполнительных операторов. Эти операторы отличаются тем, что обслуживают в основном вычислительные процессы и не содержат сложных элементов тактического выбора альтернатив при организации размерной сети. Основными являются алгоритмы вычисления параметров размерной сети при различных типах размеров. Эти алгоритмы используют разветвленную сеть стандартных подпрограмм и операторов.

Таким образом, алгоритмы нанесения размеров на чертежах организуются в иерархическую систему программ различного ранга и назначения. Система имеет свои внутренние управляющие программы. Для удобства понимания иерархической организации данной системы в заголовок схемы каждого алгоритма вводятся символы, отображающие уровень данного алгоритма в иерархии. Символом Р обозначается управляющая программа; П - программа; п/п - подпрограмма; СТ - стандартная подпрограмма (оператор); ТО - тактический оператор; ИО - исполнительный оператор. Символы в заголовке схемы располагаются по убыванию рангов. Перед символами ставится двухзначное число, обозначающее номер программы. Например: 02П01-обозначают, что Б комплексе управляющей программы 02 имеется программа 01; 01Р02 обозначает, что управляющая программа 02 входит в комплекс управляющей программы 01 и т. д.

Схемы алгоритмов управляющих программ

Схема алгоритма 01Р нанесения размеров на комплексном чертеже изображена на рис. 57. Как известно, комплексный чертеж состоит из нескольких изображений, структура которых и методика получения в той части, которая может влиять на размеры, одинаковы. Семантически изображения делятся на два класса: основные виды и виды (или выносные элементы). В основных выделяется главный вид. Обслуживание каждого вида ведется одним и тем же комплексом алгоритмов, который управляется программой 01Р02. В зависимости, от класса изображения его массиву в памяти присваивается метка П,- (i = 1, 2, ...,-6) - для основных видов; В,- (i =1, 2, ...) - для видов.

Виды комплексного чертежа обслуживаются в следующем порядке:

основные виды в порядке возрастания индекса (i = 1 присваивается главному виду);

виды сначала дополнительные, затем местные в порядке возрастания индекса.

В схему рис. 57 включены счетчики /ц и J- Первый обеспечивает выход из алгоритма при J = 2, т. е. после обслуживания видов обоих классов. Счетчик обеспечивает заканчивание работы по данному классу и переход на очередной (содержанием этих счетчиков являются числа, показывающие количества видов данного класса).

В схему алгоритма 01Р входит управляющая программа 02Р, которая воздействует непосредственно на различные программы нанесения размеров.

Схема алгоритма 01Р02 показана на рис. 58. Процесс нанесения размеров на чертеже при выбранном исходном размерном графе, показывающем связи между размерами и базировку, может быть разделен на две части: во-первых, формирование размерной сети,

[Началоj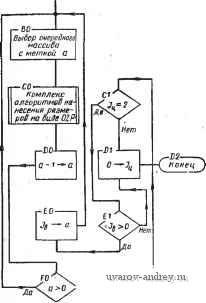

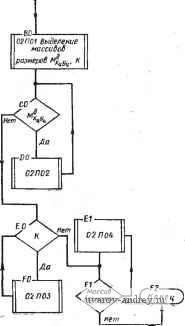Рис. 57. Схема алгоритма 01Р нанесения размеров на комплексном чертеже Рис, 58. Схема алгоритма 01р02

включающее в себя размещение размерной и выносных линий; во-вторых, формирование и размещение размерной надписи. Тактика формирования размерной сети различна для двух принятых Б технике методов отсчета размеров: от одной базы и цепочкой, Б которой конец предыдущего размера является началом для последующего. В первом методе можно вьщелить процесс, в котором общей базой для отсчета размеров служит точка (например, общий центр семейства дуг окружностей). Нанесение размеров Б этом часто встречающемся случае имеет свои особенности.

Все изложенное диктует необходимость образования трех самостоятельных программ формирования размерной сети и размещения размерных надписей:

02П02 - программа, обслуживающая семейства концентрических дуг и окружностей;

02П03 - программа, обслуживающая линейные и угловые размеры при координатном методе нанесения;

02П04 - программа, обслуживающая цепочки размеров.

В комплекс 02Р входит также программа 02П01, которая носит служебный характер и формирует массивы с присвоением им меток очередности обработки. В первую очередь обрабатываются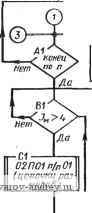

T-fi -

Перенос кода д заглавную ячейку массива

Формирование а-.п; л'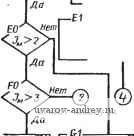

Формирование а:п,п',х^у^

Формироваиие а-- п, п',х„у.

Переадресация 1на i-дублиро вание базы;пе-реадресаиияЗд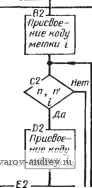

Формирование адреса b в массиве очеред-ности оЬравотки

Переадресация команд обзора по п наочеред-нук> ячейку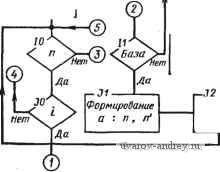

.А3±-.

Переадресация команд обзора на очередной код

г-СЪ 0-

к-*а{.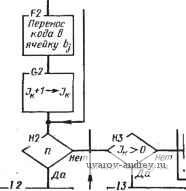

Стирание кода в заглавной ячейке массива. Метка i

Присвоение массиву метки базы

Переадресация Кода i т свободные разряды

Рис. 59. Схема алгоритма 02П01 классификации размерной информации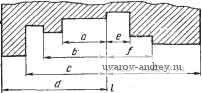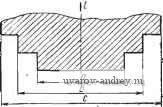

Рис. 60. Йассивы с одним и тем же базовым ограничением Рис. 61. Ось симметрии как базовое ограничение

массивы, обслуживаемые программами 02П02 и 02П03. Этим массивам присваиваются метки М^у^ (ХпУи - координаты общего центра) и К соответственно. Массивам, обслуживаемым программой 02П04, особых меток не присваивается. Таким образом, 01П02 вырабатывает импульсы для включения в работу и адресации по массивам программ обслуживания. В комплекс 01Р02 можно условно включить стандартные программы общего назначения, например, преобразования координат, построения общих элементов для пересекающихся дуг и т. п. Обращение к этим программам происходит на уровне конкретных программ размещения размеров.

Схема алгоритма 02П01 показана на рис. 59. Эта программа является входной в комплексе 01Р02. Задачей ее является классификация размерной информации по видам баз и формирование соответствующих массивов. При формировании массивов с меткой К (общее базовое ограничение) возникают некоторые стандартные ситуации. Первая из них показана на рис. 60. Здесь массивы размеров а; Ь; с; d я е; /; г имеют одно и то же базовое ограничение /. Однако принятое нами направление обхода обслуживаемого контура (внутренность контура всегда слева) вносит в эти массивы признак, позволяющий отличить их друг от друга. Так, для массива а; Ь; с; d линия / содержит конечные точки размерных линий, а для массива е, f, г - начальные.

Вторая ситуация показана на рис. 61. Общим для всех размеров а; Ъ; с базовым ограничением служит ось симметрии. При кодировании такая ось должна быть снабжена специальной меткой базы .

Наконец, третья ситуация, включающая в себя несколько типичных случаев, показана на рис. 62. Здесь размер а определяет протяженность АС, которая не является элементом контура. Другим типичным случаем является вхождение какого-нибудь размера (например, г на рис. 62) в несколько массивов размеров, каждый из которых объединен своей базой (на рис. 62 такими массивами являются а; b и с; d; е; /).

В ходе работы 02П01 формируются критерии классификации. Ими являются: содержание счетчика Jq и специальной ячейки