Если это условие не выполнено, то ребро ложное, и оно либо удаляется из описания, либо снабжается соответствующей меткой J7 , С другой стороны, удаление того или иного ребра может повлечь за собой удаление вершины, так как каждая вершина инцидентна не менее чем трем ребрам. Эти рассуждения и реализуются в алгоритме.

Выше говорилось, что чтение чертежа включает в себя процесс анализа и процесс узнавания. Рассмотренные алгоритмы реализуют процесс анализа. Рассмотрим теперь алгоритм узнавания оригинала по его проекциям.

Алгоритм узнавания оригинала по его проекциям

Модель узнав'ания мы рассмотрим как процесс установления ассоциативных связей между некоторым алфавитом простейших оригиналов и геометрическими фигурами которые могут быть проекциями этих оригиналов (рис. 40). Если закодировать упомянутые алфавиты в виде массивов, например, так, как показано на рис. 47, то ассоциации легко программируются. Код оригинала, состоящий из одного числа, ставится в соответствие с тройкой чисел, каждое из которых является кодом проекции этого оригинала на одну из плоскостей проекций в схеме Монжа (или проекций одного из положений оригинала относительно плоскости проекций в используемой нами геометрической схеме построения чертежа). Таким образом, коды оригинала можно рассматривать как условные точки, определяемые тремя координатами в неко-

МассиВ 1

массив 2

Рис. 47, Коды для распознавания оригинала по чертежу

{начало)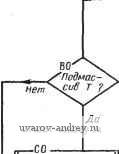

Распознавание тел по проекциям

Выделение массивов для основного алгоритма

чтение чертежа.

Составление матрицы смежности

Выделение циклов с метками V и п

Ндзначение меток

а и Г

Удаление из массива ао.лопшып. ребер и вершин

Окончательное д]ормирование массива П.О.

{Конеи, J

Рис. 48. Управляющая программа чтения чертежа: Л - коды распознавания тел; Я. О. - пространственный образ {символ BI; С/)

тором Пространстве оригиналов, в массиве 1 коды оригинала дополнены взятыми из массива 2 кодами их комплексных чертежей, состоящих из трех проекций. При этом легко заметить, что некоторые подмножества оригиналов образуют в упомянутом пространстве геометрические места точек, которые можно использовать для упрощения процесса узнавания. -

Упомянутое пространство является фазовым, в нем возможны области, не заполненные .точками. Однако из массива / видно, что первые четыре оригинала располагаются в этом пространстве в плоскости, перпендикулярной оси IIi, на прямой, проходящей через начало координат и делящей угол между координатными плоскостями, определяемыми осями П^Па и П1П3, пополам. Очевидно, что любое тело вращения с осью, перпендикулярной плоскости Пц будет точкой, расположенной в этой же плоскости; Пятый и шестой оригиналы массива 1 расположены также в плоскости, перпендикулярной оси П^, но с координатой 5. Приведенный анализ показывает, что оригиналы в приведенном алфавите можно узнать, по одной из проекций, например по фронтальной. Исключение составляет кольцо и полукольцо, где необходимо включить в рассмотрение вторую проекцию. Поменяв местами проекции в полукольце, можно исключить этот случай.

Алгоритм узнавания можно построить как процесс выбора по коду одной из проекций либо как процесс выделения подмассивов.

Последний процесс допускает работу в более обширном алфавите. Например, выделяется подмассив с кодами горизонтальной проекции в виде 1 , затем поиск ведется внутри этого подмассива по признаку кода фронтальной проекции. Кодам каждого оригинала необходимо отнести стандартные программы вычерчивания любых изображений этих оригиналов. Одним из положительных качеств принятого подхода является возможность обогащать алфавиты оригиналов и фигур в ходе экспериментирования с программой. Выходом алгоритма узнавания является выделение по коду оригинала массива его пространственного образа, который затем может быть использован алгоритмами анализа.

Рассмотренные выше алгоритмы чтения чертежа объединяются в систему управляющей программой, схема которой показана на рис. 48. Работа йачинается с определения необходимости применения алгоритма распознавания оригинала по его проекциям. Такая необходимость может быть заложена в задание. Следует еще раз отметить, что в условиях применения дискретной техники, где гладкие кривые могут быть представлены в конечном счете только в результате их кусочно-линейной аппроксимации, применение алгоритма узнавания ограничено. Расширение его применения связано с развитием алфавитов оригиналов и соответствующих фигур, а также стандартных алгоритмов вычерчивания.

В результате последовательного применения изложенных алгоритмов формируется окончательный массив пространственного образа. В этот массив входит:

массив пространственных координат л;,-, у г,- точек оригинала;

матрица смежности точек в оригинале;

массив циклов из рёбер оригинала с метками Г , да,

п. ;

матрица инцидентности ребер циклам.

Глава VI. АЛГОРИТМИЧЕСКОЕ РАЗМЕЩЕНИЕ И НАНЕСЕНИЕ РАЗМЕРОВ НА ПРОЕКЦИЯХ ЧЕРТЕЖА ПРИ ИСХОДНОМ РАЗМЕРНОМ ГРАФЕ

1. ОСНОВНЫЕ ПОНЯТИЯ и ОПРЕДЕЛЕНИЯ. ЭВРИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА РАЗМЕЩЕНИЯ И НАНЕСЕНИЯ РАЗМЕРОВ

Одной из особенностей задачи размещения и нанесения размеров на чертеже является возможность более полно использовать в качестве основы для формальных моделей соответствующие ГОСТы. Последние отражают наиболее положительный практический опыт и содержат, очевидно, оптимальные с точки зрения этого опыта рещения. В ГОСТах изложено большинство тех эвристик, которые зарождаются как правила решения неформальных задач в результате накопления опыта. Стандарты ЕСКД выгодно отличаются от предыдущих стандартов тем, что в них учитываются нужды автоматизации. Однакоправила ГОСТов составлены, конечно, в расчете на использование их человеком, который имеет в памяти обширный комплекс геометрических,. технологических, конструкторских и других знаний, в совокупности именующихся инженерными. Это позволяет человеку применять правила ГОСТа как основу для формирования творческого решения в ходе процесса графического конструирования. В связи с проблемой использования рекомендаций ГОСТ в процессе автоматизации их можно разделить на две категории:

1) однозначные правила, которые могут быть использованы в алгоритме непосредственно;

2) правила, нуждающиеся в дополнении, которое, во-первых, превращает их в однозначные для множества оригиналов, обслуживаемых алгоритмом, и, во-вторых, позволяет создать числовую модель.

Приведем примеры правил и рекомендаций, используя ГОСТ 2.307-68 Нанесение размеров и предельных отклонений .

Пример из первой категории

2.2. При нанесении размера прямолинейного отрезка размерную линию проводят параллельно этому отрезку, а выносные линии - перпендикулярно размерным.

Другой пример

2.12. Не допускается использовать линии контура, осевые, центровые и выносные линии в качестве размерных.

В этих правилах вся информация однозначна и легко переводится в числовую модель, так как используются понятия параллельности, перпендикулярности, отрицания, импликации.

Пример из второй категории

2.9. Выносные линии должны выходить за концы стрелок размерной линии на 1 ... 5 мм.

Илидругойпример

2.49. При большом количестве однотипных элементов изделия! неравномерно расположенных на поверхности, допускается координатный способ их нанесения с указанием размерных чисел в сводной таблице.

У человека не возникает серьезных затруднений в применении таких рекомендаций. Однако он будет поставлен перед необходимостью решить вопросы: в рекомендации 2.9 - выбор какого-то определенного числа из ряда 1 ... 5; в рекомендации 2.49 - можно ли отнести конкретное количество однотипных элементов к категории большое , достаточно ли неравномерно они расположены на поверхности и т. д. В алгоритмическом решении все эти вопросы необходимо-определить точно в зависимости от каких-то параметров. Допустим, выбор чисел из ряда 1 ... 5 по мере возрастания можно ограничить только целыми числами, а затем поставить в зависимость от абсолютных размеров проекции. При этом надо разработать формулу, по которой можно будет вычислять нужное число. Можно также использовать эвристический выбор какого-нибудь определенного числа.

С еще большими сложностями приходится иметь дело, когда уточняются понятия, выражаемые словами: большой , маленький , простой , сложный , удобный , наглядный и т. п. В то же время пункты 2.29; 2.31; 2.33; 2.36. ГОСТ 2.307-68 основывают выбор способа нанесения размера на анализе именно таких понятий. Отметим, что кроме неопределенностей отмеченного типа существуют процессы, которые в машинном решении имеют большое значение, а в ГОСТ либо не оговорены вообще, либо оговорены весьма расплывчато. Например, ГОСТ 2.307-68 предлагает (п. 1.2): общее количество размеров на чертеже должно быть минимальным, но достаточным для изготовления и контроля изделия.

В этом пункте, совершенно правильном по существу, отсутствует указание на способ определения такого количества размеров. Причина проста: этот способ далеко нетривиален, он до сих пор полностью не разработан и не описан в точных и достаточно простых выражениях, хотя логическая и математическая основа такого метода имеется. Это теория параметризации геометрического объекта. Решение всех отмеченных неформальных задач может быть получено с помощью эвристического моделирования.

Ё сйлу того, Что гост оставляет Некоторую неопределённость на пути к формальной модели, приходится проводить итерационный эксперимент для выяснения среды задачи и стандартных ситуаций. В ходе разработки формальной модели процесса размещения и нанесения размеров проводились эксперименты типа фиксация и опрос . Приведем некоторые эвристики, полученные при анализе результатов таких экспериментов.

1. Конечная картина размерной сети и размещения размеров на чертеже испытуемому неясна и проясняется в ходе процесса нанесения размеров. Каждый последующий размер наносится локально оптимально по отношению к предыдущему нанесенному размеру.

2. Основной эвристикой является стремление разместить размер без добавления пересечений вновь вычерчиваемых линий с нанесенными ранее.

3. При нанесении множеств размеров выделяются массивы концентрических дуг и окружностей. Эти массивы обслуживаются отдельно.

4. Лица с производственным опытом выделяют массивы угловых размеров (75% случаев), а также габаритные размеры (80% - на комплексном чертеже, 63% - на контуре), причем габаритные размеры обслуживают в первую очередь.

5. В 100% случаев нанесение размеров начиналось с линейного размера. В 46% случаев размеры наносились от большего к меньшему.

Исходя из изложенного, были установлены стандартные ситуации и ограничения, вошедшие в формальную модель.

Ограничения, стандартные ситуации, эвристические правила

Классификация размеров. Размеры делятся на массивы линейных, угловых, размеров радиусов либо диаметров окружностей на концентрических окружностях либо дугах. Размеры также делятся по типу базового ограничения на: массивы с одним и тем же базовым ограничением (отсчитанные от одной базы); размеры, составляющие массив цепочек (конец i-ro размера является началом (i -f 1)-го размера).

Буквы и цифры. Все буквы и цифры, необходимые при нанесении размера, выбираются исходя из ГОСТ 2.304-68 Шрифты чертежные . Размер шрифта принимается постоянным для всех случаев (h = 3,5 и для нанесения предельных отклонений h = = 2,5).

Линии и надписи. Совокупность размерных и выносных линий будем для краткости называть размерной сетью. При алгоритмическом нанесении размеров следует стремиться к минимальному числу пересечений линий размерной сети, относящихся к различным размерам. Не допускается пересечения линий и размерных чисел либо надписей.

Расстояние между линиями в размерной сети и между контуром проекции и ближайшей линией принимается / ц, = 21г.

Длина стрелочного конца размерной линии / = 85, где Sft - толщина линии контура чертежа.

Пусть L - длина размерной линии. В случаях, когда L < < 2,21, считается, что стрелочные концы не размещаются на отрезке размерной линии. В этом случае можно различить две ситуации.

1. Данный размер не является элементом цепочки. В этом случае размерная линия удлиняется в обе стороны на величину 2,5/ мм, стрелочные концы поворачиваются на 180° и размещаются с внешней стороны выносных линий по отношению к измеряемому отрезку. Размерное число наносится над продолжением размерной линии либо выносится на полку. Размещение размерного числа происходит с помощью алгоритмического поиска места, свободного от ранее нанесенных линий.

2. Данный размер является элементом цепочки. В этом случае стрелочные концы размерной линии заменяются точками, а размерное число либо размещается над размерной линией, либо выносится на полку.

В дальнейшем будем называть совокупность цифр, букв и знаков, несущих информацию о размере, размерной надписью. В случаях, когда длина размерной надписи, вычисленная исходя из размеров принятого стандартного шрифта, больше чем L, предпринимается вынос размерной надписи на полку с добавлением соответствующих линий размерной сети.

Длина размерной надписи подсчитывается по формуле

~ ~Ь доп ~1~ надп!

где Lpy = (3/г -f 1) мм; k - количество цифр в размерном числе или букв в условной надписи; L оп = (2,1 мм; L a n =

= {2,5k + 1) мм.

Высота S размерной надписи с учетом промежутков и возможности наносить предельные отклонения размера принимается равной 10 мм. Таким образом, для размещения размерной надписи необходимо поле чертежа в виде прямоугольника размерами LS. Этот прямоугольник будем называть в дальнейшем размерным . Применение такого прямоугольника вместо размерной надписи позволяет экономить память машины и принимать решения в ряде случаев. Например, при нанесении размера диаметра либо радиуса внутри окружности размерная надпись размещается в случаях

с> < , а L,. <

12 V2

где R - радиус обслуживаемой окружности. Размерные надписи наносятся над размерными линиями, если считать нижней частью чертежа кромку, где размещается штамп. В случаях, когда

LLa +1 мм, средина размерной надписи смещается относительно средины L на величину

с = - 1 мм.

При этом смещение происходит вправо по нечетной размерной линии (считая от контура) и влево - по четной. Все рассуждения ведутся в расчете на масштаб изображения I : 1. В случаях другого масштаба в формулы и выкладки, где используется величина размерной линии, вводится масштабный множитель /С„.

Некоторые правила размещения размеров на проекции. Алгоритмическое описание основных операций процесса нанесения размеров. Пусть имеется некоторое изображение (рис. 49) кон-. тура М, на котором необходимо нанести размеры. Большинство размерных надписей стремятся при этом вынести за пределы контура. Можно выделить четыре зоны такого выноса, в которых возможно размещение размерной информации, не считая зоны № О - пространства внутри контура. Зоны /-4, окружающие габаритный прямоугольник, в который вписан обслуживаемый контур, располагаются так, как показано на рис. 49 (возможен, конечно, и другой порядок). Обход контура в дальнейшем условимся делать в направлении, при котором внутренность М остается слева. Такое направление будем считать положительным. Глубина используемого участка каждой зоны зависит от числа размеров, отнесенных к зоне. С точки зрения удобства чтения чертежа необходимо стремиться к минимальной глубине используемого участка каждой зоны за счет возможно равномерного распределения размерных надписей по зонам. Размеры прямоугольника, описанного около изображения (включая зоны размещения размерной информации), являются исходными величинами при компоновке видов комплексного чертежа, выбора масштаба изображения и формата чертежа.

Рассмотрим алгоритмические операторы, обеспечивающие отнесение размерной надписи к зоне размещения. Пусть необходимо нанести размер, отображающий длину некоторого отрезка прямой. Подсчитав по приведенным правилам величины L и S, получим габариты размерного прямоугольника. Вместе с элементами выноса участок, требуемый для размещения размера, составит прямоугольник высотой Я = 5 (в случаях, когда размерная надпись и измеряемый отрезок находятся по одну сторону от размерной линии) либо h = S -f /г (рис. 50), когда размерная надпись и измеряемый отрезок находятся по разные стороны от размерной линии. Определить h можно с помощью ориентации. Каждая протяженность, измеряемая размером, ориентирована нами по отношению к внутренней области фигуры, ограниченной контуром так, что она располагается всегда слева. Отсюда каждый измеряемый отрезок может быть задан упорядоченной парой точек: начальной и конечной с координатами. Это нечто иное, как вектор.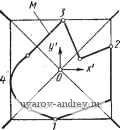

РазмернаИ надпись

О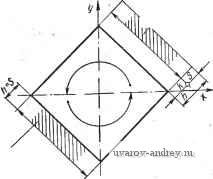

Размерная подпись

Рис. 49. Исходный -кстур для нанесения размеров Рис. 50. Элементы выноса размера

Будем сравнивать положительные направления осей координат, к которым отнесен измеряемый отрезок, и проекций на эти оси упомянутых векторов. Если проекция вектора на ось Ох отлична от нуля и совпадает по направлению с осью, то h = S. Если же при соблюдении условия отличия от нуля проекция вектора противоположна по направлению оси Ох, то h = S k.

Допустим теперь, что проекция вектора на ось Ох равна нулю. Рассмотрим проекцию того же вектора на ось Оу. При совпадении направлений вектора и оси h - S; в противном случае Я = 5 -f /г. Легко видеть, что мы реализуем процесс присвоения h = S ~{- k при условии, когда угол а,-, составленный между выносной линией и горизонтальной линией и отсчитанный в направлении обхода, лежит в пределах 0° < а,- < 180°. В то же время h = S присваивается в случаях, когда 180° < < 360°. Процесс можно организовать, измеряя угол а^-, который является к тому же признаком отнесения линейного размера к зоне размещения размерной информации. Если поместить начало координат Оху в точку пересечения диагоналей габаритного прямоугольника (рис. 49), то при 225° < а,- < 315° размер выносится в зону 315° < а,- < 45° - в зону 2; 45° <: а,- < 135° - в зону 5; 135° < а,- < 225°- в зону 4.

2. ФОРМАЛЬНАЯ МОДЕЛЬ РАЗМЕЩЕНИЯ

И НАНЕСЕНИЯ РАЗМЕРОВ РАЗЛИЧНЫХ ТИПОВ

Определение направления выноса размерной информации по отношению к контуру

Как известно, ГОСТ 2.307-68 рекомендует наносить размерные линии предпочтительно вне контура изображения (п. 2.8). Пусть (рис. 51) АВ - измеряемый отрезок а - указывает направление обхода контура. По отношению к а выносные, линии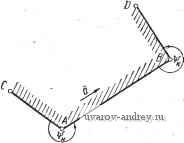

Рис. 51. Схемы выноса размера

Рис. 52. Нанесение размеров длин связанных отрезков

могут быть проведены вправо либо влево от Л Б (если смотреть по направлению а). Пусть отрезок АВ изолирован от других размерных элементов чертежа, т. е. нет смежных с ним измеряемых отрезков. Тогда выбор направления выноса размерной линии зависит от наличия свободного места на чертеже и от расположения относительно АВ остального контура проекции. Через точки А, В проводятся прямые, перпендикулярные к отрезку АВ. На некотором фиксированном для выноса расстоянии к (например, к =7, к = 10 мм) отмечаются точки, определяющие размерную линию, снабженную стрелочными концами. Выносная линия продолжается за отмеченные точки на 2 мм. Если одна из возможных (рис. 51) размерных линий, а также стороны размерного прямоугольника не пересекают других линий чертежа, то выбирается именно этот случай выноса.

Если оба варианта выноса допустимы и одинаковы с точки зрения числа появляющихся пересечений, то предпочтение отдается варианту, реализующему вынос размера от проекции . Другие более сложные случаи, а также оптимизация размещения размерных надписей рассмотрены ниже.

Пусть далее отрезок АВ связан с другими измеряемыми отрезками контура, например АС и BD (рис. 52). Будем измерять углы и % между тройками смежных отрезков, определяемых по матрице смежности. Причем измеряется угол, лежащий вне контура проекции (вращением радиус-вектора по часовой стрелке). На тактику выноса размерной линии будут оказывать влияние величины 90; 180 и 270°. Рассмотрим различные случаи и их влияние на принятие решения по направлению выноса размерной линии. В дальнейшем под индексами н и к в обозначениях углов будем понимать начало и конец образмериваемой протяженности, совпадающие с начальной и конечной точками измеряемого отрезка.

Рассмотрим различные ситуации, возникающие в зависимости от величины упомянутых углов. Будем рассматривать угол при