г л а в а V. АВТОМАТИЧЕСКОЕ ЧТЕНИЕ ЧЕРТЕЖА

1. ЭВРИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССА ЧТЕНИЯ ЧЕРТЕЖА

Процессы чтения и построения чертежа являются основными в системе графического конструирования. Они обеспечивают возможность построения различных изображений одного и того же объекта, что совершенно необходимо для технического чертежа. Пусть, например, в память ЭВМ введен эскиз некоторой детали, выполненный в виде комплексного чертежа. Требуется автоматически построить другое изббражение детали, например аксонометрию или перспективу. Для решения такой задачи необходимо прежде всего по кодам исходного чертежа восстановить пространственный образ, а затем преобразовать коды этого образа в - коды требуемого изображения.

Природа операции проецирования такова, что между двумя изображениями одного и того же оригинала стоит его пространственный образ. Анализ последнего необходим для образования структуры нового изображения. Можно, конечно, предположить, что в ЭЦВМ введено описание пространственного образа. Однако такой ввод затруднен, по крайней мере, двумя обстоятельствами: 1) большой сложностью описания пространственного образа по сравнению с описанием его проекций которые сами по себе являются очень удобным и универсальным языком; 2) трудностями представления и анализа объекта на уровне пространственного образа в силу парциальности процесса мышления, поэтому, если конструирование проводится в системе человек-машина, где оператор активно, воздействует на процесс, то лучшим языком общения здесь все-таки будет чертеж.

В силу изложенного задача автоматизации обсуждаемых процессов может ставиться следующим образом. Исходным для алгоритмов построения и чтения чертежа является некоторый обратимый чертеж объекта, введенный в память машины тем или иным способом. Этот чертеж является базой, на которой развертывается графическое конструирование. При этом в силу структурной связи

мёжДу пространственным образом И чертежом не устраняется возможность работы в случаях, когда исходным является пространственный образ. В качестве поверхностей, образующих оригинал, могут входить плоскости и каркасные поверхности. Процесс восстановления пространственного образа по заданному чертежу, т. е. процесс чтения чертежа, является сложным для формализации.

Рассмотрим более подробно модель процесса чтения чертежа. Эвристическое моделирование убеждает, что в этом процессе присутствуют тесно переплетающиеся между собой узнавание объекта по его проекциям и геометрической анализ формы и положения объекта по его чертежу. Оставляя подробный анализ этих процессов пока в стороне, укажем, что их сравнительное значение в общем процессе чтения чертежа резко колеблется и зависит от свойств изображенного объекта. Так, например, комплексный чертеж неправильного многогранника типа случайного гранного тела будет читаться в основном за счет процесса анализа, а чертеж куба - за счет процесса узнавания с последующим привлечением анализа. Обе эти стороны мышления хорошо развиты у конструктора. Они заслуживают выделения в качестве стандартных операторов процесса чтения чертежа.

Рассмотрим сначала процесс анализа, без которого не обходится чтение почти всякого чертежа. В основе модели этого процесса можно положить два положения, которые легко усмотреть из принятой геометрической схемы построения чертежа.

1. Если проекции двух точек соединены на комплексном чертеже какими-нибудь линиями на всех проекциях (либо совпадают на одной из проекций, а на других соединены), то точки соединены в пространстве (являются смежными в оригинале).

2. У двух проекций одной и той же точки, полученных вращением всей системы отнесения около одной из осей координат, координаты, отложенные по этой оси, численно равны между собой.

Учитывая изложенное, можно разработать алгоритм, который по исходным координатам проекций точек и меткам линий, проходящих через них, будет восстанавливать пространственные координаты этих точек и формировать в памяти информацию о соединениях этих точек в оригинале. В частности, любой многогранник, являющийся основой построения любой формы с помощью дискретной техники, может быть восстановлен по своим проекциям. Сложности чтения чертежа возникают при неудачном выборе видов (такой выбор может быть вынужденным). Из положения 1 вытекает, что виды исходного чертежа надо выбирать так, чтобы относительно любой пары точек, не соединенных в пространстве, была однозначная информация на чертеже (т. е. на одной из проекций пара таких точек не должна быть соединена). Такое требование можно выполнить не всегда, так как виды комплексного чертежа выбираются, как известно, из других соображений. Кроме того, при чтении чертежа, который является множеством линий.

человек Пользуется не Только понятиями начертательной геометрии. Он учитывает также некоторые общие свойства оригинала, например, непрозрачность объема объекта, замкнутость объема и т. п. Для учета всех этих особенностей в алгоритме необходимо внести их в модель чтения чертежа.

Будем называть М-средой некоторое множество, обладающее свойствами непрерывности, однородности и ограниченной проницаемости для проецирующих лучей, приводящей к возникновению невидимых на чертеже элементов. Для обозначения М-среды используем символ С^. Элементом будем полагать М-точку, обозначаемую в дальнейшем Л^, е - окрестность которой, гомеоморфная шару, есть С^.

В связи с введенными понятиями можно рассматривать два типа оригиналоб: оригинал Ф, являющийся обычной геометрической моделью физического объекта; М-оригинал, или Ф-* - оригинал, являющийся расширенной моделью физического объекта. Ф-** - это часть пространства, заполненная С^, имеющая определенную форму, размеры и объем, ограниченный от остального пространства.

Назовем М-поверхностью среду С^, состоящую из предельных точек А^, лежащих на границе между Ф'* и остальным пространством. Обозначим такую поверхность символом п'*. Введя б-окрестность, гомеоморфную кругу для точек А^ cz W, можно сказать, что любая б-окрестность для А^ cz есть п^.

Потенциально осуществимы операции выделения на множеств точек, обладающих определенными геометрическими свойствами. Это приводит, в частности, к появлению ребер R, вершин V и граней G, которые могут вызвать некоторое клеточное разбиение п^.

Потенциально осуществимы следующие операций над Ф-*.

1. Операция сечения Ф'*, которая выделяет в cz множество элементов как принадлежащих П^, так и не принадлежащих ей, но обладающих свойствами принадлежности некоторой геометрической поверхности сечения.

2. Операция разъединения Ф-* по поверхности сечения. При этом геометрическая поверхность сечения становится в разъединенных частях поверхностью п^.

3. Операция объединения нескольких Ф^ в один, при котором П' составляющих оригиналов объединяются в единую П'*. При этом М - точки в области объединения перестают быть предельными и принадлежать П'.

Некоторые свойства Ф^

1. Оригинал Ф^ всюду замкнут (по определению).

2. Любая часть оригинала Ф'*, которая может быть получена операциями сечения и разъединения, имеет точки, обладающие в е-окрестностью. Другими словами, часть оригинала, полу-

ценная сечением и разъединением, не может быть п'*, ребром, вершиной.

3. Любая точка, принадлежащая и не принадлежащая П', имеет е-окрестность в С^.

Некоторые свойства

1. Поверхность п' всюду односторонняя (по определению).

2. На п'* могут быть особенности, которые назовем выступами и впадинами. Наличие этих особенностей при проецировании П'* может наводить на ней клеточное разбиение (граница входа во впадину, основание выступа), дополняющие контурные линии и линии перехода.

Уточним понятия выступа и впадины с точки зрения операции проецирования. Будем рассматривать всевозможные сечения Ф-*. Тогда среди них могут найтись сечения, в которых ограничивающая фигуру сечения линия будет-иметь точки, изменяющие направление прямой, касательной к линии при переходе от одной точки этой линии к другой. Такие изменения могут привести касательную в положение параллельной направлению проецирования (либо в положение совпадающей с проецирующим лучом при центральном проецировании). В таких случаях точка касания будет принадлежать контурной линии. Геометрические места отмеченных точек будут задавать при проецировании клеточное разбиение на поверхности. На многогранной поверхности клеточное разбиение дополняется вершинами и ребрами. Ребра и вер- шины могут также получаться при операциях разъединения либо объединения Ф-*.

Множество Ri cz (i = О, 1, 2, k) при условии Rg = R назовем гранью трехмерного клеточного разбиения.

Основные положения, связанные с оригиналом Ф^

Пусть имеется сечение Sj оригинала Ф^ плоскостью. При этом рассечены ребра R. Рассмотрим граф сечения Г^, в котором

будут вершинами, а ребрами будут линии пересечения плоскости с поверхностями, представляющими собой внутренность граней клеточного разбиения.

Сформулируем следующие положения.

1. Если Rir, то она входит в один из циклов графа. Доказательство следует из свойства 1 оригинала Ф'*.

2. Пусть Р (А) - степень вершины А в графе Г^. Тогда, если Р (r = 2, то rj cz Rj является сечением П^. В самом деле, если предположить, что одно из ребер (г^ либо г^) не лежит на П^, то Rf не является вершиной телесного угла, но тогда R не лежит на п^, а это противоречит свойству 3 оригинала Ф^ (рис. 32).

Рис. 32. Анализ ребер графа сечения оригинала

Рис. 33. Случай, когда степень вершины графа сечения больше двух

---7

Рис. 34. Случай вложения одного цикла в другой

3. Пусть Р -(Rf) = 2 -f п, где п - произвольное целое положительное число. Тогда через R проходит п ребер, являющихся сечениями геометрических поверхностей, не обладающих свойствами П^. В самом деле, допустим, что ребра 1 к 2, инцидентные Rf (рис. 33), представляют собой сечения n . Пусть далее через R проходят также ребра 5, 4, ... Тогда вследствие свойств Ф и П' один и только один из углов а либо р может быть заполнен (т. е. .быть телесным). Пусть телесным будет угол а, тогда ребра 3 и 4 не могут принадлежать П', так как не являются граничными в Ф^. Пусть далее телесным будет угол р, тогда ребра 3 н 4 не могут принадлежать П' по тем же причинам, что и в первом случае.

4. Пусть (рис. 34) Rf в входит в несколько циклов, вложенных друг в друга. Тогда, по крайней мере, одно из ребер г, Г^, не входящее в объемлющий цикл, не является сечением П'. Доказательство следует непосредственно из основного назначения быть границей и из свойств 1 и 3 оригинала Ф'.

Если сечение не содержит ни одной F и ни одного г, то графы (рис. 35) не могут быть графами сечения оригинала Ф^. Сечение рис. 35, а противоречит свойствам операции сечения. Можно, конечно, направить поверхность сечения так, чтобы она проходила только через ребро Rj оригинала. Но тогда поверхность сечения вырождается в ребро R. В случае, представленном на рис. 35, б, операциями сечения и разъединения можно выделить ребро которое содержит точки, не имеющие е-окрестности, что противоречит свойствам Ф^. Рассмотрим некоторые случаи, когда имеет несколько циклов. Объемлющим будем называть цикл, который не вложен ни в какой другой цикл. Внутренним назовем цикл, который вложен в другой цикл, являющийся для него объемлющим. Рассмотрим ребро rf, входящее в объемлющий цикл Г^. Будем считать, что через ребро rf проходит несколько циклов, если они отличаются друг от друга ребрами, смежными хотя бы с одной вершиной rf. Множество циклов, обладающих

Рис. 35. Примеры графов, ие являющихся сечениями оригинала:

а - пример противоречия свойству операции сечения: б - пример выделения ребра Рис. 36. Граф, состоящий из одной компоненты связности

ЭТИМ СВОЙСТВОМ, назовем связкой циклов при rf. Число циклов в связке обозначим А (rf) и будем называть порядком связки.

5. Если входит в объемлющий цикл и связка при имеет порядок А (rf) = 1, то является сечением П^. Действительно, из положения 1 вытекает, что ребро г^. должно входить хотя бы в один цикл Г^. Так как этот цикл является объемлющим, то он делит точки плоскости сечения на внутренние, находящиеся в оригинала, и внешние. Точки рассматриваемого ребра будут, следовательно, граничными между точками и точками окружающей оригинал среды. Отсюда ребро - сечение П' .

Положение 5 касалось случая, когда ребро сечения входит в объемлющий цикл. Рассмотрим теперь случаи, когда не входит в объемлющий цикл. Здесь могут быть две ситуации:

1) состоит из одной компоненты связности и rf, таким об- разом, связано с ребрами объемлющего цикла;

2) состоит из нескольких компонент связности и не связано с ребрами объемлющего цикла.

Ситуация 1. Проанализируем возможные случаи. Выделим одну из вершин ребра объемлющего цикла, где заканчивается маршрут,. соединяющий это ребро с исследуемым. К этой вершине подходят два ребра объемлющего цикла, которые как сечения определены положением 5. Здесь возможны случаи:

а) оба ребра объемлющего цикла не есть сечения П';

б) оба ребра объемлющего цикла есть сечения П^;

в) только одно из ребер объемлющего цикла есть сечение П'.

В случае а подсчитаем степень вершины, общей для объемлющего цикла и рассматриваемого ребра. Если степень не больше четырех, то все ребра, не входящие в объемлющий цикл, будут, сечениями П^. Если же степень вершины больше четырех, то вычеркиваем ребра объемлющего цикла и к двум ребрам, входя-

щим в объемлющий цикл после вычеркивания, применяем положение 5.

В случае б все ребра, отличные от ребер объемлющего цикла, не есть сечения П'.

В случае в подсчитываем степень вершины объемлющего цикла. Если она больше трех, то поступаем, как в случае а, когда степень вершины больше четырех. Когда степень вершины не более трех, то ребро, отличное от ребер объемлющего цикла, есть сечение П'. Легко видеть, что вследствие замкнутости объема можно определить таким образом два ребра маршрута, смежные с двумя вершинами объемлющего цикла (рис. 36). Пусть А к В - вершины объемлющего цикла, а rf и - ребра графа, определенные как сечения. Допустим, что исследуется ребро rf. Могут быть случаи:

а) rf и rf не есть сечения П^, тогда весь маршрут, включая rf, не есть сечение П';

б) rf и rf есть сечения П^, тогда степень вершин маршрута не превышает двух, в этом случае весь маршрут есть сечение П'; степень хотя бы одной вершины маршрута более двух, в этом случае через вершины rf проходит несколько маршрутов, соединяющих Л с Б. В последней ситуации из множества циклов, проходящих через вершины rf, отыскиваем объемлющий. Ребра, входящие в него, являются сечениями П'. Напомним, что все сказанное относится к ситуации 1, когда состоит из одной компоненты связности.

Ситуация 2. Пусть ребро rf входит во внутренний цикл, не связанный с объемлющим. Этот внутренний цикл может быть сечением полости, если число объемлющих его циклов будет нечетно, но может быть и сечением оригинала в случаях, когда число объемлющих его циклов четно (рис. 37). При анализе отдельных ребер внутреннего цикла, объемлющие циклы не учитываются и к анализируемому циклу применяется положение 5. Вследствие бесконечности форм материального мира полнота системы предложений, показанных выше, не может быть доказана без ограничений. Однако следует отметить, что все предложения носят топологический характер и, следовательно, не накладывают ограничений на форму поверхностей. Что же касается ограничений, которые разумно было бы ввести, то, во-первых; характер современного производства накладывает ограничения на применяемые поверхности; во-вторых, в большинстве задач, разрешаемых человеком в процессе ГК в системе человек-машина, достаточно информативными оказываются многогранные поверхности.

Рассмотрим модель процесса узнавания. Мы говорили о том, что информация на чертеже может быть выражена только линиями. Рассмотрим некоторые множества линий на чертеже и соотнесем

Рнс. 37. Граф-, ссстсящий из нескольких компонент связности Рнс. 38. Структура чертежа

0,1,

ИХ с множеством возможных оригиналов, которые могут быть ими отображены. Введем определение. Структурой на чертеже будем называть множество линий, которые могут отображать пространственные элементы, пересекающиеся по элементу, размерность которого на единицу меньше. В этом смысле пары пересекающихся-линий, плоскостей, поверхностей образуют структуры. В то же время прямая и плоскость, например, не образуют структуры. С помощью структур можно задавать сеть, которая является отображением клеточного разбиения оригинала. Это не значит, что с помощью элементов, .не составляющих структур, нельзя задавать, например, сетку многогранника. Но в таком случае необходимо будет решать дополнительные позиционные задачи для того, чтобы перейти к проекциям сетки многогранника.

Рассмотрим некоторые примеры простейших структур. Проекции двух пересекающихся прямых на чертеже образуют структуру, так как может быть построена точка пересечения этих прямых. Легко представить себе условия, при которых множество прямых отображает пересекающиеся в пространстве плоскости. Для отображения двух фронтально-проецирующих плоскостей, пересекающихся по прямой Ь, достаточно множества прямых а, Ь, с, изображенных на рис. 38. В то же время это множество может отображать три плоскости, составляющие трехгранный угол с вершиной в точке В. Задание на прямых а, Ъ, с трех произвольных точек ведет к возможности отображения с помощью этой структуры объемного тела - тетраедра. Структура, показанная на рис. 39, отображает пять плоскостей, линии пересечения которых образуют линейную структуру чертежа. Применяя эвристики М-оригинала, мы приходим к выводу, что ни один из циклов здесь не является отверстием. Таким образом, процесс узнавания состоит в том, что устанавливается ассоциативная связь между линейной структурой чертежа и некоторым, известным заранее

02 = у 2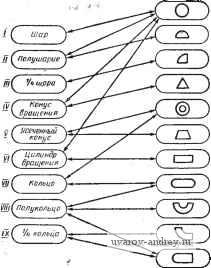

Рис. 39. Структура'объемного тела на чертеже

Рис. 40. Ассоциативные связи в процессе узнавания объекта' по чертежу

оригиналом, который может быть отображен этой структурой. У технически грамотного человека такие ассоциативные связи существуют между множествами вещей и геометрических фигур, которые могут быть изображениями этих вещей. Формально это может быть представлено в виде двух массивов, а также некоторого множества меток, отображающих ассоциативные связи.

Пусть, например, набор вещей состоит из следующих объектов: шар; полушарие; четверть шара; прямой круговой конус; прямой круговой усеченный конус; прямой круговой цилиндр; кольцо; половина кольца; четверть кольца. Пусть далее существует набор геометрических фигур, входящих в чертеж в качестве проекций. В этот набор включим окружность; половину окружности, ограниченную ее диаметром; четверть окружности, ограниченную двумя взаимно перпендикулярными радиусами; треугольник; две концентрические окружности; трапеция; прямоугольник; прямоугольник с двумя скругленными полуокружностями и короткими сторонами; полукольцо. Наметим ассоциативные связи между этими наборами так, чтобы каждый элемент из первого набора был связан с тройкой геометрических фигур второго набора, которые могут составить трехкартинный комплексный чертеж, отображающий только ассоциированный с этой тройкой предмет. На схеме (рис. 40) связи между элементами наборов показаны стрелками. Образы чертежа, как это видно из схемы ассоциаций, обладают различной силой по отношению к процессу распознавания вещи по чертежу.

2. ОСНОВНОЙ АЛГОРИТМ ЧТЕНИЯ ЧЕРТЕЖА Постановка задачи

Пусть на обратимом комплексном чертеже задано некоторое множество линий, отображающих клеточное разбиение на поверхности оригинала. Будем рассматривать клетки разбиения, заданного на чертеже. Содержание внутренней области каждой клетки может быть либо поверхностью П' (тогда это часть среды С^), либо геометрической поверхностью (тогда это вход в полость, в канал, имеющийся в оригинале). Если выявить содержание внутренней области каждой клетки, то можно распознать все части оригинала и отличить трехмерные клетки, заполненные средой, от геометрических трехмерных клеток. Этим будет распознана топологическая структура оригинала, что является наиболее сложным в чтении чертежа. Восстановление формы оригинала и его размеров для случая, когда он отнесен к системе координат, базируется на возможности восстановления пространственного положения множества точек оригинала и их соединений. Если такие соединения выполнить отрезками прямых, товосстанавливается некоторая многогранная поверхность, аппроксимирующая оригинала. Эта поверхность может быть взята за основу для вывода изображения.

Исходным для алгоритма, который будем называть основным, является трехкартинный комплексный чертеж оригинала, построенный по геометрической схеме, изложенной выше. С этого чертежа снимаются и кодируются только данные о точках и линиях, которые могут быть сняты с него автоматическим устройством. Относительно каждой точки, которая на чертеже является результатом пересечения каких-либо линий, должно быть известно следующее:

координаты проекций точки на каждом поле чертежа;

метки линий, которые проходят через точку чертежа.

Если имеются п видов чертежа, то в памяти ЭЦВМ формируются п списков, определяющих каждый из этих видов как плоские узоры из линий и точек их пересечений на чертеже. Результатом работы алгоритма являются координаты точек в пространстве, проекции которых были введены в машину, а также матрица смежности точек, содержащая информацию о том, какие точки необходимо соединить линиями. Таким образом, восстанавливается каждая клетка клеточного разбиения оригинала. Если необходимо восстановить структуру оригинала (например, распознать отверстия, определить видимость линий и т. д.), то необходимо иметь дополнительную информацию об оригинале. Эта информация может быть автоматически получена из тех же исходных данных с помощью процессов:

формирования циклов, расположенных в одной грани М{, и меток v, показывающих число объемлющих циклов для формируемого цикла;