слабым местом является то обстоятельство, что дерева целей, или графа решения для человека, приступающего к решению задачи, не существует. Если же оно существует, то в большинстве случаев можно по дереву составить обычный алгоритм с применением эвристик как средств достижения известной цели. В отечественной литературе изложен новый принцип программирования, применяемый к задачам оперативного управления. В основе этого принципа лежит понятие модели решения. Разработан аппарат формирования модели на основе специальных процедур, которые позволяют получить модель из формализованного описания объектов управления и процессов, происходящих в них. По сравнению с лабиринтным методом решения задач в эвристическом программировании этот метод является несомненным шагом вперед.

Наконец следует упомянуть еще об одном подходе. Речь идет об эволюционном программировании, которое заменяет процесс моделирования человека моделированием его эволюции. Эволюционное программирование основано на случайном поиске в заданном множестве возможностей. Основным элементарным актом здесь является предсказание. На основе изучения символов среды в прошлом и настоящем требуется предсказать последующий символ. Алгоритм предсказания и является моделью разумного поведения , разумного организма . Эволюция заключается в самоусовершенствовании алгоритма предсказания. Процесс эволюции моделируется путем адаптации предсказывающего алгоритма, параметры которого улучшаются- при помощи случайного поиска. Таким образом можно рассматривать только весьма простые задачи предсказания. В реальных задачах усложнение проблемы предсказания может привести к качественным изменениям эволюционного программирования. В подобных случаях трудно отделаться от искушения использоьать имеющийся опыт человека. Необходимо только этот опыт получить. Само по себе описание объектов, участвующих в неформальных задачах, а также описание процессов, идущих в них, весьма трудно.

В применении к задачам графического конструирования для создания формальной модели необходимо описать поведенческие операции, которые отображают процесс решения. Это описание наталкивается на значительные трудности. Дело в том, что логическое обоснование цепи действий при решении неформальной задачи основывается на интуиции. Устойчивые модели решения неформальных задач возникают в результате большого практического опыта. При этом сам процесс решения автоматизируется и превращается в навык. Человеку, владеющему таким навыком, трудно отдавать себе отчет в своих действиях при решении задачи. Возникает противоречие: наибольшей информацией об алгоритме задачи должен обладать человек с большим опытом решения таких задач, но ему то как раз и трудно восстановить в сознании этот алгоритм. Вместо обоснованной цепи действий у него в сознании

присутствует некоторая упрощенная схема, сохраняющая только основные инструкции для действий в различных ситуациях. Эти инструкции вспоминаются только в случае, когда появляются соответствующие ситуации. Простейшим примером такого свертывания процесса в навык является вполне грамотное письмо образованного человека, не вспоминающего в процессе письма правил грамматики.

Для получения информации в обсуждаемых случаях обычно используют специальные эксперименты. Наиболее простыми из них являются.самонаблюдения. Возможность такого самонаблюдения (интроспекции), при котором познающий и познаваемый объекты как бы совпадают, обеспечивается распределением внимания и памятью протекших событий. При самонаблюдении мы должны иметь двоякое волевое направление внимания: во-первых, на содержание, на предметы, с которыми связан эксперимент и наше переживание и, во-вторых, на само переживание. Как подтвердили исследования психологов, такое направляемое волей раздвоение внимания невозможно в один и тот же момент времени. Однако возможно быстрое чередование направлений внимания. Быстрота такого чередования может быть настолько велика, что переживания не будут успевать распадаться в памяти. Опыты показывают, что последовательные образы памяти длятся от 8 до 20 с, что .обеспечивает возможность наблюдения за ними и составления на основании этого суждения о тех подлинных переживаниях, следами которых являются эти образы.

Все изложенное показывает возможность применения интроспекции в таких экспериментах, но все-таки она сопряжена с большими трудностями и имеет ряд недостатков, особенно в применении к нашим целям. Эти недостатки сводятся к тому, что самонаблюдение оказывает неблагоприятное влияние на те переживания, за которыми ведется наблюдение. Вследствие этого испытуемый не в состоянии правильно передать .свои переживания, так как решение, входящее в отчет, происходит только на уровне сознания (ход решения необходимо комментировать). В реальной же ситуации подключается интуиция. Темп решения при интроспекции искусственно замедляется и прерывается отчетом.

Недостатки, обнаруженные в самонаблюдении, побудили к поискам другой методики экспериментов и привели к объективным наблюдениям. Имеется много разновидностей методики объективного наблюдения за поведенческими актами. Отметим, что в случае графического конструирования непосредственным отображением хода решения задачи является чертеж, что облегчает в ряде случаев задачу объективного наблюдения. В качестве описания наблюдений очень распространено протоколирование поведения испытуемых в ходе решения задачи. Однако при этом исследователь сталкивается с большим многообразием форм поведения и с трудностями переработки информации, содержащейся в протоколах.

3. МЕТОД ЭВРИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ

При подготовке экспериментов, проводимых с целью сбора информации, необходимо учитывать наличие определенной уста новки испытуемых. Давно замечено, что реакция организма не является только непосредственной функцией стимула, она обусловлена также промежуточными факторами. Последние связаны с состоянием системы, на вход которой оказывается воздействие. При решении любой задачи поведение выступает в форме последовательности действий, ориентированных в направлении решения. При этом совершенно необходима внутренняя согласованность реакций в соответствии со смыслом ситуации, что обеспечивает наличие определенного избирательного отноп1ения этих реакций к конечному результату. Такая согласованность реализуется в виде определенной готовности к действию по решению конкретной задачи, что и является установкой. Создание целесообразной для эксперимента установки повышает активность испытуемого и увеличивает вероятность выявления приемов, используемых в ходе решения задачи, и той цепочки действий, которая характеризует адаптивное поведение при решении.,

С целью создания благоприятной установки испытуемого эксперименты должны быть естественными. Под естественным экспериментом мы понимаем наблюдение или опыт, проводящийся в естественной обстановке для той деятельности, которая моделируется. Испытуемый не инструктируется специально и не знает, что участвует в эксперименте. Получается эффект, сходный с феноменом скрытой камеры , применяемым в кинематографии. Широко известно, что такой метод позволяет получать информацию, которую невозможно получить обычным путем.

Формализация задач ГК может базироваться на экспериментах по крайней мере трех типов, которые можно условно назвать фиксацией , опросом ,- обучением . Эксперименты первых двух типов предполагают определенную подготовленность экспериментатора, которая заключается в предварительном моделировании решения задачи. Рассмотрим подробнее такое моделирование.

Будем называть множество факторов, имеющих отношение к разрешаемой задаче, средой задачи. Возможное конкретное сочетание факторов, соответствующее определенному моменту времени и месту, назовем ситуацией. Целенаправленное поведение в среде задачи заключается в выборе ситуации для движения к ре-, зультату. Это движение происходит в виде перехода отодной ситуации к другой либо путем трансформации исходной ситуации. Весьма полезны часто встречающиеся (типовые для данного класса задач) ситуации, выявляемые статистикой экспериментов и данными опыта решения подобных задач. Подготовка экспериментатора начинается с изучения среды задачи. Происходит ознакомление с возможными исходными данными, промежуточными данными, а также с элементами, которые могут войти в решение. Выявление

Рис. 2й. Схема выбора разрезй

Нет

Начало

Анализ чертежа но предмет необходимости разреза

Выделение Видов, на которых

необходимо выполнить разрез

т

Определение, числа и поло-/кения секущих плоскостей, организующих разрез Выявление частичных разрезов

Построение фигур сечения и проекций с разрезами

Нет

Проверка достаточности разрезов

Коне Ц J

ситуаций, а также предварительная их классификация на типовые и возможные проводится после ознакомления со средой задачи. При этом привлекается собственный опыт, литературные источники и другая информация, доступная экспериментатору на этом этапе. В ходе подготовки могут возникать неясные моменты, которые формулируются в качестве возможных вопросов, выявляемых с помощью эксперимента.

Обычным приемом, организующим всю подготовку, является составление дерева решения задачи. При этом используется последовательное разбиение задачи на все более мелкие части. В результате

такой подготовки у экспериментатора возникает собственное впечатление о задаче и о возможном алгоритме ее решения. Иногда в ходе подготовки удается составить достаточно содержательную схему алгоритма. Тогда можно считать, что неформальная задача решена алгоритмически с помощью процесса самонаблюдения. Однако гораздо чаще во многих блоках такой схемы содержится информация о том, что надо сделать, а не о том, как надо сделать. Наличие предварительной схемы позволяет неясности и вопросы также связать в некоторую логическую последовательность. Возникает дерево, целей планируемого эксперимента.

Приведем, пример подготовки эксперимента. Поставим задачу алгоритмизации процессов* организации разреза на техническом чертеже. Под такой организацией понимается выбор типа разреза, числа и положения секущих плоскостей разреза. Анализ литературных источников приводит нас к схеме, изображенной на рис. 28. Составить такую схему можно и без изучения литературы, если экспериментатор имеет представление и некоторый опыт построе--ния и чтения технических чертежей. Вместе с тем очень важным условием успешности дальнейшей работы является знакомство экспериментатора с особенностями программирования для ЭЦВМ. В этом случае он может легко стать на точку зрения машины и понять, какая информация ей необходима в каждой конкретной ситуации. Схема, представленная на рис. 28, может быть исполь--зована человеком, но не машиной. Планирование эксперимента

по дополнению этой схемы можно выполнить по результатам ее анализа. Прежде всего процессы блоков 1, 2, Зиб представляются далеко неясными и неформализованными. С другой стороны, процесс блока 4 формализуется сравнительно легко. Построение фигуры сечения при заданной секущей плоскости в оригинале сводится к позиционной задаче на пересечение, разрешаемой с помощью средств аналитической геометрии. Построение проекций с разрезами сводится к преобразованиям координат точек и также выполняется на основе формальной геометрической схемы.

Заключение о формализуемости блока 4 не означает того, что программирование процесса этого блока - легкая задача.-Здесь могут встретиться трудности в составлении программ, однако экспериментального выявления процесса в этом случае не требуется. При сопоставлении блоков 1, 2, 3, 5 бросается в глаза то обстоятельство, что они связаны между собой неявным присутствием некоторого признака необходимости разреза. Этот признак является инвариантом при переходе от одного блока к другому и является одной из целей для экспериментального выявления. В зависимости от содержания этого признака будет проводиться и глобальный анализ чертежа и,выделение видов, на которых необходим разрез. Этот же признак влияет на вид разреза. Как известно, признаком необходимости разреза является наличие в оригинале внутренних полостей, форма и размеры которых не могут быть выявлены только проецированием по какому-нибудь направлению. Для алгоритмического решения необходимо уметь по проекциям комплексного чертежа (если последний является исходным в задаче) либо по описанию оригинала устанавливать наличие такого признака.

Проведем теперь планирование эксперимента. Изложенный выше анализ будем считать нулевым уровнем информативности, который кладется в основу первого эксперимента. В дальнейшем планирование последующих уровней эксперимента происходит по типу итерационного процесса. Таким образом, для t-ro эксперимента исходной является схема решения задачи, полученная в результате (i - 1)-го эксперимента. Будем называть такой эксперимент естественным итерационным.

Рассмотрим методику упомянутых трех типов эксперимента.

Фиксация. Эксперимент по этому типу заключается в том, что испытуемый получает задание, в ходе которого ему приходится решать формализуемую задачу или ее часть. Экспериментатор наблюдает за испытуемым и фиксирует его действия шаг за шагом, не вмешиваясь в процесс.

Опрос. В этом опыте экспериментатор ведет себя активно. Используя свою подготовленность, он создает установку, управляет испытуемым, нацеливая его на решение того вопроса, который, выявлен при планировании эксперимента. Вопросы должны быть максимально упрощенными, конкретными. Они не должны тре-

бовать сложной аргументации, привлечения многих данных, многопланового мышления. Сложность вопроса не всегда можно оценить до эксперимента. Иногда простой вопрос вырастает в проблему. В таких случаях необходимо строить дерево внутри этой проблемы, разбивая вопрос на более простые подвопросы. Под простыми в экспериментальной ситуации мы понимаем такие вопросы, которые требуют либо односложных ответов, либо простейших графических или логических операций типа: провести линию , отметить точку и т. п. Если, например, спросить у испытуемого: С чего начинать оснащение чертежа разрезами? , то этим вопросом можно поставить испытуемого в затруднительное положение, так как ему придется, не имея конкретного примера, обобщать собственный опыт. Такое обобщение входит в задачу экспериментатора и выполняется в ходе итерационного экспери-. мента после каждого проведенного уровня с целью выявления параметров процесса и его особенностей. Накапливаются также мелкие особенности, отражающие редко встречающиеся, но принципиально возможные ситуации.

Обучение. В этом опыте экспериментатор ставит себя в положение ученика, а испытуемого - в положение учителя. При этом на нулевом уровне экспериментатору необходимо получить только те сведения о задаче, которые необходимы для понимания им обучающих действий учителя. Положение учителя, в которое ставится испытуемый, обычно создает благоприятную эвристическую установку. Учитель старается, чтобы ученик прошел все те этапы, которые были пройдены в свое время испытуемым. В ходе обучения вспоминаются и различные интересные ситуации, а также рецепты поведения в них. С другой стороны, опыт по составлению программ и установка на алгоритмическое описание-задачи обеспечивает со стороны ученика постепенное наращивание сведений, которые кладутся им в основу алгоритма. Коренное отличие обсуждаемого типа эксперимента от других заключается в том, что здесь моделируются не только поведенческие, но и мыслительные акты. Экспериментатор анализирует в ходе эксперимента свою мыслительную деятельность. Тогда как в процессе экспериментов типа фиксация или опрос рассматриваются и анализируются поведенческие акты испытуемого, которые являются функцией его мыслительных актов.

Рассмотрим процесс создания модели в ходе итерационного эксперимента и алгоритм последнего. Поскольку эксперимент направлен на выяснение вопросов, которые возникли в процессе подготовки очередной итерации, информация получается двух типов:

1) информация, запланированная заранее как ответ на поставленный вопрос;

2) информация, которая является неожиданной с точки зрения плана эксперимента, но освещает какие-то неучтенные вопросы моделируемой задачи.

при обработке информации прежде всего выделяют ty, которая характеризует допустимое решение. Факт допустимости решения вытекает из того, что получен результат (например, графическое построение), который может быть использован как ответ на вопрос, поставленный в задаче. Как известно, в отношении числа решений все задачи могут быть разбиты на две категории: а) задачи с единственным решением; б) задачи, имеющие множество решений. Результат решения задачи а является оптимальным. В случае задачи б возникает проблема оценки и сравнения различных решений и факторов, характеризующих наилучшее решение и ведущих к нему. Группировка данных и факторов, характеризующих наилучшее решение, обеспечивает формулирование функции цели и процесса оптимизации. В задачах а может быть поставлен вопрос об оптимизации процессов решения, ведущего к единственному решению. Примером задачи а в ГК являются позиционные и метрические задачи на чертеже. К задачам б относятся задачи выбора оптимального аппарата проецирования при построении наглядных изображений, задачи на управление формой геометрических объектов, задачи на размещение геометрических объектов в т. д.

После выделения информации, характеризующей допустимое решение, следует сгруппировать данные, которые необходимы как исходные для получения допустимого решения. В этот раздел включают числовые данные, ограничения и т. п. Отметим, что ограничения в сложных случаях играют значительную роль в формальной модели. Бывают случаи, когда учет ограничений приводит к противоречивым ситуациям. Для разумного выбора в подобных случаях необходимо заранее оценить важность каждого ограничения в разрешаемой задаче. Список исходных данных может дорабатьшаться в процессе создания формальной модели и алгоритма. Наконец, исследуется множество конкретных ситуации, которые наблюдались в ходе итерационного эксперимента. Часто эти ситуации составляют иерархию, которая в конце концов превращается в дерево взаимосвязанных стандартных операторов и подпрограмм, поэтому очень важно устанавливать причинные связи, обусловливающие переход из одной ситуации в другую, а также инварианты различных процессов, происходящих во время решения. Выделение этих инвариантов в дальнейшем также ведет к созданию алфавита стандартных операторов, которые применяются по специальным правилам, составляющим язык общения. Примером таких операторов является, допустим, оператор вычисления коэффициентов уравнения плоскости по ее параметрам; оператор вычерчивания линии со стрелочным концом при алгоритмическом нанесении размеров и т. д.

Все изложенное является основной задачей экспериментатора в ходе формирования эвристической модели по результатам эксперимента. В конце работы выписываются приемы решения, носящие чисто эвристический характер, т. е. эвристики. Последние кла-.

Рис. 29. Пример чертежа детали с полостями

дутся в. основу выбора там, где формальные подходы получить не удалось. Примером эвристики является такое, например, соглашение: считать оптимально размещенным размер, в котором размерная надпись располагается как можно ближе к измеряемому объекту (не ближе расстояния, предусмотренного ГОСТом), а нанесение размера вызывает минимальное число пересечений вновь вычерчиваемых линий с имеющимися на чертеже .

Работа по созданию эвристической модели требует массовости экспериментов и статистической обработки материалов. Во всех случаях необходимо выделять те части модели, которые доведены до состояния формализуемых математическими средствами. Таким образом, эвристическая модель превращается постепенно в формальную модель и является основой для алгоритма.

Приведем пример работы над эвристической моделью. Используем рис. 28, где изображена схема, являющаяся результатом подготовительной работы экспериментатора, нулевого уровня эксперимента. Рассмотрим блок / схемы. Содержание этого блока, возможно, понятно для специалиста чертежника. Однако оно совершенно непригодно в качестве основы для алгоритма. Проанализировав это содержание, поставим задачи и вопросы для следующего уровня итерационного естественного эксперимента. Признаком необходимости разреза является наличие в оригинале полости, которая не может быть показана видимой на выбранных видах. На чертеже (рис. 29) видно, что изображена деталь с полостями. Но что такое видно ? Необходимо перейти к такому признаку, который мог бы быть выражен числом. По смыслу операции проецирования и внутренней полости можно заключить, что признаком наличия полости является невидимость некоторых линий при одновременной многосвязности контура. Причем для применения этого признака необходимо уметь восстанавливать по чертежу пространственный образ полости, так как упомянутые признаки на различных проекциях могут относиться к различным пространственным образам. Возникают задачи: а) уметь различать факт многосвязности проекции (если, конечно, многосвязность не закодирована специально); б) уметь находить пространственный образ любо.й части оригинала, пользуясь его проекциями.

Рассмотрим задачу а. Она возникает, когда в качестве исходного берется описание чертежа. Если контур анализируемой проекции многосвязен, то он графически состоит из ряда циклов, связанных друг с другом или вложенных друг в друга. В рассмат-

Пространственный образ

Что принято за элемент?

Т

Как соотнести метд совой коды проекции элементов и сдюрми-

ровать код пространственного образа?

обход элементов

Порядок обхода

Выделение части оригинала

С какой проекции начинать ?

т

Как соединить пространственные образы элементов ?

Каковы операции соотнесения?

т

Как получается структура оригинала

(в каком виде) г

Типичные трудности. Составление библиотеки трудных примеров

Рис. 30. Схема планирования эксперимента

риваемых ситуациях циклы вложены друг в друга. Следовательно, задача а разбивается на две части: 1) нахождение цикла в массиве кодов проекции; 2) различение случаев вхождения цикла в цикл. Заметим, что эти части формальны, и их решение с помощью обычных математических приемов не встретит особых затруднений. Изложенное иллюстрирует своеобразную тактику спуска от эмпирических рассуждений к формальным построениям. При этом задача последовательно разбивается на подзадачи по принципу дерева целей. Из блока / (рис. 28) остается задача б, которая на первый взгляд трудно формализуема. Возникает ряд вопросов: с чего начать восстановление пространственного образа? каков порядок работы (обход элементов чертежа)? что принять за элемент? Эти вопросы являются исходными для планируемого эксперимента.

На рис. 30 представлена схема планирования эксперимента. Общая схема t-ro уровня эксперимента (итерационного эксперимента) показана на рис. 31. При экспериментах типа фиксация вопросы адресуются экспериментатором как бы себе самому. Ответы черпаются из наблюдений за испытуемым. В ряде случаев приходится подбирать специальные графические задания и предлагать их для выполнения испытуемым. В этом случае вопрос скрыт экспериментатором в графическом задании. Часто при эвристическом моделировании выбор затруднен тем, что недостаточно ясна относительная важность факторов, влияющих на выбор. При этом полезна многократная имитация моделируемой деятельности. Рассмотрим, например, блоки 2 я 3 схемы на рис. 28. Выделение видов и назначение разрезов является процессом, где противостоят две тенденции: открыть полость, показать ее внутренность (при этом нарушается внешний вид оригинала на проекции); сохранить внешний вид детали на проекции. Факторы,

Рис. 31. Схема итерационного эксперимента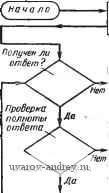

Предъявление Вопроса i-eo уровня

Зачисление ответа в актив факторов алгоритма

Имеются, вопросы?.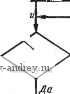

Нет

СконецЛ

Предъявление

очередного вопроса i-го уровня

регулирующие выбор в таком процессе, требуют для своего выявления массовых экспериментов и классификации ситуаций, выделения инвариантов и т. д. После такой работы возникает воз--можность перейти к количественным оценкам и построить соответствующие шаги алгоритма. Построенная в конце концов схема алгоритма является внешней по отношению к ЭВМ Для облегчения программирования составляется внутренняя схема, учитывающая особенности конкретной ЭВМ, распределение памяти и т. п.