тогда после подстановки получаем

Г + Ду = Х^Х^, + Х^ Дх, + Х^ Дх2 + ДХ1ДХ2.

Так как

Y = Х.Х^ и Дх, Дх2 О,

Ду ~ Х^ Дх, + Х^ Дх2. Таким образом, уравнение линеаризованной модели имеет вид Ду = Кл Дх, + К2 А-2.

где

1 = Х^, К2 - 1-

Тот же результат может быть получен с помощью разложения в ряд Тэйлора

Пример 2. Линеаризуем функцию

Полный дифференциал равен

dy = 2х,Х2 dxj + х? dx.

Заменим дифференциалы конечными разностями вблизи рабочей точки

Ду =2А'1А'2Дх1 + Х?Дх2.

Используя второй метод линеаризации, находим

Ду = (X, + Дх,)2 {Х2 + Дх2) - XIX2.

Отбрасывая члены второго порядка малости, получим тот же результат:

Ду = 2А',А'2Дх, + А'Дх2.

Пример 3. Найдем линеаризованную передаточную функцию тахометра [141*], упрощенная схема которого показана на рис. 1.2-1.

Уравнение момента относительно точки опоры или центра вращения О имеет вид

Л1с< 2 (Л + / sin е) / cos е - {Мх + Dx + Сх) Л cos е = Же/С Следовательно,

+1$та)-Мх+DX + CX +Mc-j~jl

Пусть рабочая точка имеет координаты X, Qo, в. В первом приближении угловыми отклонениями можно пренебречь, т. е.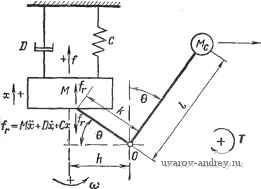

Рис. 1.2-1. Функциональная схема тахометра.

считать, что 9с=:0,О ~ 0. Таким образом, сила, записанная в левой части уравнения, может быть выражена следующим образом:

Для малых отклонений вблизи рабочей точки имеем де

/? = (/г4-/sinG) A;.

Кроме того, сила является линейной функцией смещения, поэтому

Д = Ж Дх -f D Дх + С Дх.

Применяя преобразование Лапласа, получим окончательно hX(s) 2McRQo АЙ (s) Msi + Ds + C

1.3. АЛГЕБРАИЧЕСКАЯ ЛИНЕАРИЗАЦИЯ

При малых значениях Дл; для наиболее часто встречающихся нелинейных функций одной переменной целесообразно применять приближенные формулы, приведенные в табл. 1.3-1 [48*. 121*].

Таблица 1Я-1

Первоначальное выражение

1 + Да: (1 + Длг)

/1 + Адг

f 1 + 1

f 1 + Да: в а

1п(1 + Да:)

бшДлг, shhx arsh Длг, arcsin Им

cos Дх ch Дх arch hx, arccos Дл:

tg Дат, arfh Дл: arth Aj;, arcth tx

Приближенное выражение

Первый отбрасываемый член

1.4. ЛИНЕАРИЗАЦИЯ ХАРАКТЕРИСТИЧЕСКИХ КРИВЫХ

Часто нелинейные зависимости не могут быть выражены в математической форме и задаются только графически с помощью характеристик. Тем не менее и в этом случае можно выполнить линеаризацию путем замены отношения дифференциалов отношением конечных разностей [28*, 92*].

На рис. 1.4-1 показан пример линеаризации функции одной переменной. Заменяя кривую ее касательной в рабочей точке, приближенно можно написать

м

или

м

(1.4-2)

Теперь коэффициент усиления равен отношению конечных разностей, взятых на отрезке с серединой в рабочей точке:

Таким образом,

м

Ly~KAx.

(1.4-3)

(1.4-4)

Графический метод линеаризации можно распространить на функции многих переменных. В этом случае вместо частных про-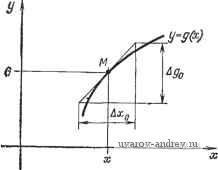

Рис. 1.4-1. Графическая лииеаризацич функций одной переменной.

изводных рассматриваются частные разности, а вместо полного дифференциала - полная разность. Например, для функции двух переменных имеем

Д V- Л-

м

(1.4-5)

Коэффициенты усиления являются отношениями частных разностей

Дл:,о м'

(1.4-6)

(1.4-7)

В результате получаем

Ду = /С, ДХ! + Ki Ах-

Соотношение с двумя переменными редко представляется в виде пространственных графиков. Обычно предпочитают изображать ряд кривых на плоскости, при этом одна переменная

играет роль параметра. В этом случае коэффициенты линеаризации опять можно определить сравнительно простым способом.

Заметим, что при рассмотрении функции, зависящей более чем от одной переменной, наклон должен выбираться независимо от всех переменных, за исключением одной.

Пример. На рис. 1.4-2 приведены анодные и сеточные характеристики триода. Определим линейную аппроксимацию вблизи рабочей точки при заданных анодном напряжении Vp=250 В, анодном токе /р=8 мА и сеточном напряжении Vq--8 В [28*].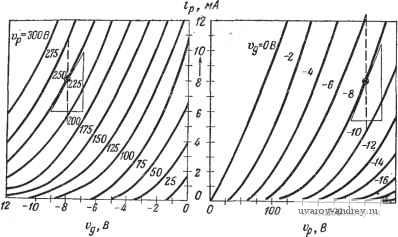

Рис. 1.4-2. Анодные и сеточные характеристики триода.

Из рис. 1.4-2 видно, что крутизна (коэффициент усиления тока) при постоянном Vp равна

10 мА -6 мА 4 мА д, -(-7 В)-(-9 В)--1

В то время как величина, обратная динамическому анодному сопротивлению (коэффициенту усиления напряжения), при te=const равна

10,5 мА-5.5 мА 5 мА , д , 275 В-225 В ~50~В=

(Следовательно, динамическое анодное сопротивление равно 10000 Ом.)

Из уравнения (1.4-5) получим следующее выражение для изменения анодного тока вблизи рабочей точки:

Например, изменения сеточного напряжения At>g=2 В и анодного напряжения At>p==-25 В вызывают, согласно линеаризованному уравнению, изменение анодного тока, равное

Мр = 2 мА/В-2 В-0,1 мА/В.25 В =-Ы,5 мА.

Следовательно, измененное значение анодного тока будет равно 9,5 мА. При t>p = 225 В и t>g=-6 В характеристики дают точное значение, равное 9,6 мА.

Наконец, отметим, что линеаризованные коэффициенты усиления можно определить, используя только один тип характеристик. Например, с помощью анодных характеристик получим

12,4 мА - 4,8 мА 7.6 мА . . , gm- бВ-(-10В) =-1ГВ-=9 /В-

а с помощью сеточных характеристик -

1 10,7 мА-5,5 мА 5.2 м А .

Гр 276 В -225 В - ЖВ

Отклонения не являются большими, а точность практически приемлема.

1.5. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ЛИНЕАРИЗАЦИИ ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ

Допустим, что переменная у управляемого процесса определена в m выборочных точках вблизи рабочей точки М. В дальнейшем будем предполагать, что у зависит от п независимых сигналов и переменных состояния. Пусть, далее, т>п. Связь между переменными опять зададим функцией вида

y = g{xi, Х2.....х„). (1.5-1)

Зависимая переменная в рабочей точке равна

V = g{Xi, Х„ Х„). (1.5-2)

Известны значения зависимой переменной в т произвольных выборочных точках вблизи рабочей точки М:

y,-g(1л, X ,){kh2, .... т). (1.5-3)

Разности между координатами выборочных точек и рабочей точки представим в виде

X i. - Х„ - Ax

(k=l,2, ...,т) (1.5-4)

К,-К = Ду, (k = \, 2, т). (1.5-5) Предположим опять, что линеаризованная модель имеет вид

- 2 Ki Ах,. = КАх,+ ... +Кп (1.5-6)

Составим теперь сумму квадратов отклонений для выборочных точек, используя коэффициенты линеаризованной модели и выходы модели и нелинейного элемента:

т

Е=(Кг х + /С^ Дх2, -Ь ... Ч- КпХпп - Ду,). (1.5-7)

Необходимое условие минимума суммы квадратов Е состоит в том, что все первые частные производные равны нулю:

Отсюда получаем

т

-щ-2(К, Дх + Кгх, -t- ...+/< Д; , - Ду,) Дх = О

(г = 1, 2, ... , ft), (1.5-9) или, поделив на 2 и сделав алгебраические преобразования,

mm т

/С, 2 Д-1й Xik + /Сг S Дхгл Дх,. -f ... + АГ 2 Д. й lXik = ft=i ft=i ft=i

= ДДу,Дх;, (г = 1,2.....ft). (1.5-10)

Коэффициенты линеаризации Кг (г=1, 2, ..., п) можно определить из системы п уравнений (1.5-10), если выборка корректна (т. е. если детерминант системы уравнений ие равен нулю). Для функции одной переменной y=g(x) уравнение линеаризованной модели имеет вид

где коэффициент линеаризации или эквивалентный коэффициент усиления равен

2 hkxu

2 CkY

m> 1.

(1.5-12)

Для функции двух независимых переменных у = г/(д?!, хг) уравнение линеаризованной модели имеет вид

Ау ~ Ki Axi + К2 Ах,

где

/га \ ( \ / \ / \

j m \ I m \ / m \

(1.5-13)

/ / / \ft=l

ft=I / \k=l / \k=l I

(1.5-14)

Если нелинейная связь выражается аналитически, суммы можно заменить интегралами [141*], например в случае нелинейной функции y=g(x) от одной переменной

J bg(Lx)bxd(hx) -ДХ

Г (Lxfd{Lx) - дх

(1.5-15)

Те же процедуры можно выполнить для двух и более переменных.

Метод наименьших квадратов значительно сложнее ранее описанных методов, и поэтому он редко применяется на практике.

Пример 1. Определим передаточную функцию тахометра [141*] по методу наименьших квадратов. В примере 3 разд. 1.2 было найдено, что

при малых отклонениях вблизи рабочей точки

рде f = M(,RQb Сделаем упрощения, используя это выражение

ДЛ = Л!с/?(2ЙоА'< + (А' )2). Уравнение линеаризованной модели должно иметь вид

д/, л:до).

Коэффициент усиления можно определить из уравнения (1.5-15)

J Mc/?(2QoA<o-Н (Дсо)2)Д(ой(Д(о) J (Да1)2й{Дю)

После интегрирования имеем

~ 2/з (дад)з---/Ki(;/<LJo.

Таким образом, метод наименьших квадратов в этом случае приводит к тому же результату, что и касательная аппроксимация, так как сила является квадратичной функцией от угловой скорости.

Пример 2. Линеаризуем соотношение у = g(x) = X

вблизи рабочей точки ХФО- Касательная аппроксимация дает

х=Х

и, следовательно,

Ду = nX - Дх.

По методу наименьших квадратов находим Г + Ду = (X + Дх) .

Следовательно,

К

Ду = (X -f Дх) - Х .

J {{X + Дл:) - X) Дл: (Длг)

J (Дл:)2й(Дл:)

После интегрирования получаем

rn + I

2 a(2/-l) -+W+

где квадратные скобки обозначают целую часть величины. Если = 1, то К=1. Если /2 = 2, то

Таким образом, метод наименьших квадратов и касательная аппроксимация приводят к одному и тому же результату- Если n=S, коэффициент усиления

зависит, кроме X, также от отклонения ДХ, и поэтому отличается от коэффициента усиления, полученного при касательной аппроксимации. Аналогично если п=4, то

Таким образом, различие между обоими методами существует, и оно будет обнаруживаться и при п>4.

1.6. ПЕРВЫЙ ТЕСТОВЫЙ МЕТОД ЛЯПУНОВА

Хорошо известно (разд. 1.3 ч. I), что с помощью введения фазовых переменных и переменных состояния любое нелинейное дифференциальное уравнение порядка п

jcC )=/(x, л, ..- , . - ) (1.6-1)

можно свести к совместной системе нелинейных дифференциальных уравнений первого порядка

Xj =/i(Xi, Х2, ... , х„)

. (1.6-2)

или К нелинейному векторному дифференциальному уравнению

x=f(x). (1.6-3)

Допустим, что нелинейность выражается однозначной аналитической функцией. Тогда в рабочей точке равновесия М

X = \Х\ Х<, .... ,