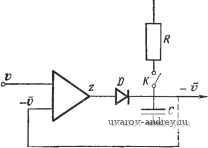D становится проводящим и конденсатор С заряжается отрицательно до тех пор, пока v и v опять совпадут. В электрическую

схему вводят катодный или

эмиттерный элемент, позволяющие устранить влияние других элементов.

Возвращаясь к экстремальной системе, показанной на рис. 3.2-3, заметим, что z=v- -V возрастает от нуля. Когда Z достигает некоторой границы Z, X начинает изменяться в противоположном направлении. Другая часть оптимальной системы может быть сходна со схемой на рис. 3.2-4. Для уменьшения шума сигнал сможет поступать на вход интегратора. Тогда переменная х будет меняться в обратном направлении, если только интеграл от z, т. е. площадь Az (рис. 3.2-9), достигает некоторой величины VTi. Так как v = Q, получаем

TI2 Г/2

= J 2:(0fl = J -О {t)dt = Vr (3.2-33)

где V - максимальное смещение v(t). Отметим также, что импульс, необходимый для замыкания переключателя К цепи, показанной на рис. 3.2-10, может быть получен из триггерной цепи Т. Уравнения (3.2-11) и (3.2-33) приводят к выражению

Рис. 3.2-10. Схема простого запоминающего устройства.

(3.2-34)

Так как уравнение (3.2-12) все еще применимо, должно иметь место также равенство

Г=6П (3.2-35)

Кроме того, если в системе имеются временные задержки, то амплитуда колебаний опять будет возрастать, а соответствующие кривые сдвинутся вправо.

Оптимальная система с прерывающимся поисковым процессом. Колебания около точки максимума или минимума часто недопустимы. В этом случае поиск должен быть прекращен после достижения экстремума и снова начат только в заранее определенных интервалах, когда будут иметь место некоторые отклонения [11-14]. Такая система легко реализуется, например, если дополнить триггерную цепь системы, показанной на

рис. 3.2-2, клапанной цепью. Эта цепь управляется, например, с помощью Z через функциональный генератор таким образом, что она будет закрыта и предотвратит передачу сигнала и (т. е. сделает ы = 0) всякий раз, когда z достаточно близко к нулю или, другими словами, когда -Z<z<Zi. где Z, - пороговое значение. Этот тип систем обычно называют оптимальной системой со случайным поиском.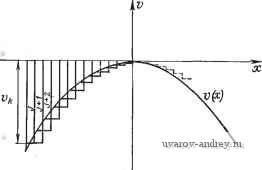

Рис. 3.2-11. Принцип работы оптимальной системы шагового типа.

Шаговые системы. В простейшей шаговой экстремальной системе [15--17] среднее значение Vm переменной v определяется на /-м шаге по формуле

vj~ J vjdt, (3.2-36)

у

где Tl - длительность шага. В данном случае среднее значение заменяет кривую v = v(x) на {j+l)-M шаге (рис. 3.2-11). Достижение экстремума обнаруживается только на следующем шаге. Чувствительный элемент воспринимает разность Vm,j-i - Vmj. Если она меньше зоны нечувствительности элемента, никакой реакции не будет. Поэтому зона нечувствительности должна быть как можно меньше.

3.3, АНАЛИЗ КВАЗИСТАЦИОНАРНЫХ ПРОЦЕССОВ

Для иллюстрации вычислительных трудностей проанализируем квазистационарный процесс оптимальной системы [1, 7, 8, 15], блок-схема которой приведена на рис. 3.3-1. Система или объект Р состоит из нелинейного элемента Л' и линейной систс'

мы Lp с единственной постоянной времени

v = g{x), Gp{s) .

Дифференциальное уравнение объекта имеет вид

(3.3-1)

(3.3-2) (3.3-3)

Мы хотим найти значение х, при котором v достигает своего максимума. Нелинейный управляющий элемент С будет изме-

Рис. 3.3-1. Общая блок-схема оптимальной системы.

пять знак сигнала и (абсолютная величина которого равна постоянной f/o) всякий раз, когда величина w отличается от максимальной Wm на величину больше некоторой величины А:

и; - да = Д. (3.3-4)

Линейный входной элемент Ц задается интегратором Oi{s)i

Таким образом,

0.(s) = .

= -f liil = -f = С

(3.3-5) (3.3-6)

Оптимальный процесс в плоскости состояний. Описанную выше оптимальную систему можно проанализировать в плоско-

сти состояний, уравнение траекторий состояния имеет вид

~±-]r[g{x)-w\, (3.3-7)

где Т = UqTJTi > 0. Ясно, что w имеет экстремум при

g{x) = w, (3.3-8)

так как тогда dw/dx=0. Характеристика v-g(x) показана в плоскости состояний на рис. 3.3-2. Эта кривая является одновременно статической характеристикой управляемого объекта,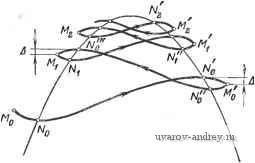

Рис. 3.3-2. Оптимальный поисковый процесс в плоскости состояний.

так как для постоянных значений w=g(x). Допустим, что вначале рабочая точка системы находится в точке Мо и в общем случае не лежит на кривой g(x). Кроме того, предположим, что входной сигнал и интегратора положителен. Тогда выражения (3.3-6) и (3.3-7) берутся с положительными знаками, и так как в точке Мо имеем g(x) - ш<0, то dw/dx<0. Начальный отрезок Моо траектории состояния убывает. В точке Л^о имеем dw/dx=0, и, следовательно, w - минимум. После этого g(x) - ш>0 и dwldx>0. Траектория состояния будет возрастать до Л^о, где dw/dx=0, к w- максимум. Вдоль отрезка No М'о траектория опять идет вниз. Если w уменьшится на Д, то знак

и изменится на противоположный. Первый полупериод завершается в рабочей точке М'о . Во втором полупериоде величина X убывает при уменьшении v, затем возрастает и снова убывает вдоль отрезков М'о Ао, АоЖхдо точки В этой точке заканчивается вторая половина цикла, и знак и снова меняется на противоположный. Обе половины цикла вместе определяют точечное преобразование, переводящее Мо в В точке Mi начинается новый цикл, который заканчивается в Ms и т. д. На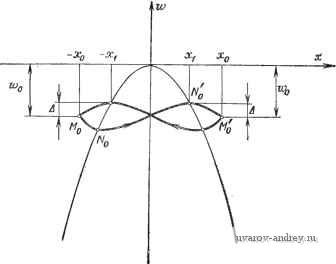

Рис. 3,3-3. Предельный цикл оптимальной системы в плоскости состояний-

рис. 3.3-2 видно, как траектория приближается к предельному циклу, который соответствует фиксированной точке точечного преобразования.

Обратим внимание на взаимное пересечение траектории, причиной которого является изменение знака и. Траектории, идущие вправо и влево, представляются на отдельных листах. Двухлистная плоскость состояний является по существу, как отмечает Казакевич, вырожденным трехмерным пространством состояний, так как третья переменная и может принимать только два значения +Ип и -Uo. Если перемена знака осуществляется с помощью триггерной схемы, то, учитывая ее постоянную времени, можно проиллюстрировать процесс в пространстве состояний. Если же постоянной времени пренебречь, достаточно будет двухлистной плоскости состояний.

На рис. 3.3-3 показан предельный цикл. Для простоты предположим, что кривая g(x) симметрична относительно оси ординат, а максимум находится в начале координат. Тогда, полагая в выражении (3.3-7)

g(x) = -x2,

уравнение для траекторий состояния для первого отрезка можно записать в виде

+ = (3.3-9)

Общее решение имеет вид

W = + (22 + с,х + Со). (3.3-10)

Подставляя это выражение в дифференциальное уравнение (3.3-9), получим С2 = - 1= Ci = 2T, Со=-2Т^. Учитывая, что значение w = Wo достигается при х=Хо, можно также определить значение А и окончательно получить

w = (Wo-\- 272 2Тхо + х2)е-<-- > - 27 + 2Тх - (3.3-11)

Изменение движения на противоположное для предельного цикла происходит при условии, что

~x\- = Wo, (3.3-12)

где

- х2 = да (- xi) = (0 + 272 - 2Тхо + х2) +с) г

-2Т^-2Тх-х\. (3.3-13)

Решение в точке х = -Хо, W = Wq имеет вид

Щ = (®o + 272 - 27хо + 4) ез-о/ 272 - 2 7хо - 2 (3.3-14)

Из последних трех уравнений можно найти значения Wq, xq, Xi с помощью решения некоторых трансцендентных уравнений. Подобный анализ можно проводить и для управляемых объектов высшего порядка, однако тогда решение будет еще сложнее. Поскольку точные вычисления требуют больших затрат времени даже для относительно простых систем, на практике предпочитают приближенные методы (такие, как гармоническая линеаризация или метод описывающих функций).

Анализ сходимости предельных циклов. Другой важной проблемой является сходимость или устойчивость предельных циклов [15]. Пусть в общем случае в п-мерном пространстве состояний Xft i и Xft обозначают состояние соответственно в начале и в конце k-ro цикла {Xk может обозначать также состояние в начале {k+l)-ro цикла). Пусть эти состояния связаны пХп-мер-

ным соотношением

*(Xfe-i) = g(x (3.3-15)

где f и g-в общем случае трансцендентные функции. Если предельный цикл существует, то

x i = Xft = Xo (3.3-16)

является решением уравнения

f(xo) = (xo). (3.3-17)

Выясним теперь, является ли предельный цикл асимптотически устойчивым. Ограничиваясь малыми возмущениями у^, можно написать

Xft = Хо + у;. (3.3-18)

Допуская, кроме того, что f и g-аналитические функции в окрестности Хо, можно разложить их в степенные ряды:

\ , di

f(xo) + -

Ук-1+ ... =g(Xo) +

у,+ ... (3.3-19)

О

Отбрасывая члены высших порядков и учитывая уравнение (3.3-17), получим в качестве первого приближения

dg dxi

(3.3-20)

(3.3-21) (3.3-22)

Последнее уравнение является линейным дифференциальным уравнением. Условие устойчивости заключается в том, что все корни характеристического уравнения

i г! - А] = О (3.3-23)

лежат внутри круга единичного радиуса с центром в начале координат комплексной плоскости, т. е.

\Zi\<l (/= 1, 2, я). (3.3-24)

3.4. МЕТОДЫ ПОИСКА В СЛОЖНЫХ ОПТИМАЛЬНЫХ СИСТЕМАХ

В многомерных оптимальных системах время, за которое требуется достичь экстремум, сильно зависит от метода поиска. В сложных экстремальных системах оптимизатор не всегда

определяет величину и направление следующего шага, осуществляемого по экстремали Q, а часто действует методом проб и ошибок [40*, 74*, 76*]. В других случаях направление следующего шага выбирается оптимизатором по градиенту к эстремумам Q. Для одномерных систем существует ряд методов для определения градиента. Направление следующего шага может определяться делением производных по времени, или с помощью синхронного детектирования с использованием синусоидальных волн, или с помощью методов с памятью и т. д. Иногда оптимизатор осуществляет регрессионный анализ. Каждый из этих методов основан по существу на необходимом условии экстремума для функции или функционала. При этом достаточные условия экстремума не всегда принимаются во внимание, хотя рассматривать их необходимо, когда имеются седловые точки.

После определения градиента находят экстремум (максимум или минимум). Для этого можно использовать следующие методы: метод Гаусса - Зейделя, градиентный метод, метод наискорейшего спуска или подъема и процедуру Бокса - Вил-сона [18].

Любая практическая реализация оптимальной системы должна удовлетворять следующим требованиям: время поиска и движения в обратном направлении должно быть как можно меньше; оптимальная система достигает экстремума с наименьшей возможной ошибкой; оборудование, используемое для управления процессами поиска и движения к экстремуму, является простым; процессы поиска и движения к экстремуму происходят правильно даже при некоторых ограничениях.

Метод Гаусса - Зейделя. Необходимое условие экстремума функции [или функционала Q(x)] имеет вид

gradQ = 4=0. (3.4-1)

В методе Гаусса-Зейделя оптимизатор определяет локальный экстремум

-11=0 (3.4-2)

последовательным изменением отдельных составляющих вектора X Для кривых Q(Xi, Хг) =Qj=const в. плоскости состояний (рис. 3.4-1) оптимизатор изменяет каждый раз одну из координат до тех пор, пока не будет достигнут частный локальный экстремум. При этом траектория достижения экстремума является кусочно-непрерывной и представляет собой лесенку из отрезков прямых, параллельных осям координат. Время достижения экстремума превышает теоретически возможный минимум.

Градиентный метод. По этому методу градиент dQ/dx определяется одновременным или последовательным измене-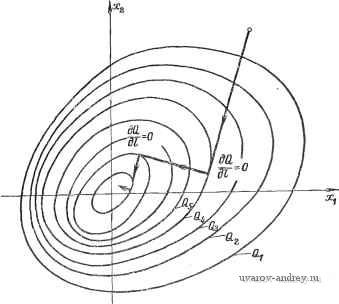

Рис. 3.4-1. Метод Гаусса - Зейделя в плоскости состояний.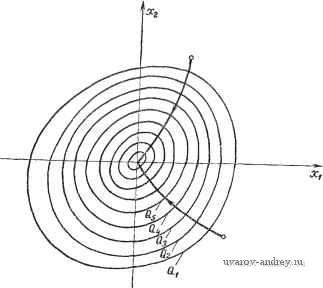

Рис. 3.4-2. Градиентный метод.

нием всех составляющих, а приближение к экстремуму происходит в направлении вектора-градиента. При одновременном изменении составляющих траектория нормальна к гиперповерхности Q{x)=Qj или в плоскости состояний к кривым Q{Xi, Х2) = = Qj (рис. 3.4-2). При последовательном изменении каждая координата изменяется на величину 6х. Оптимизатор опреде-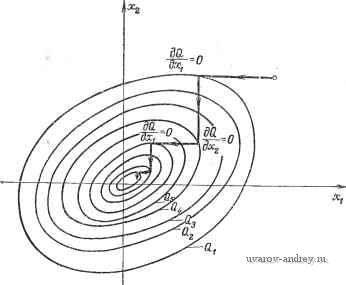

Рис. 3.4-3. Метод наискорейшего спуска (подъема).

ляет разность 6Q = Q{Xi + 6x) -Q{Xi), а затем добавляет к каждой переменной Хг приращение AXi так, что

dQ б(

(г = 1, 2, п).

(3.4-3)

Градиентный метод приводит к относительно гладким траекториям и требует немного времени для достижения экстремума.

Метод наискорейшего спуска (подъема). В этом случае процесс приближения к экстремуму опять начинается с нахождения градиента. Траектория проходит вдоль него по прямой до локального экстремума. Здесь вновь определяется градиент, и траектория следует в направлении этого нового градиента (рис. 3.4-3). Таким образом, траектория состоит из отрезков прямых линий. Метод наискорейшего спуска приводит к экстремуму за сравнительно небольшое время.

Иногда наиболее предпочтительным оказывается комбиниро-