260. Wonhara V/. iVi., Johnson C. D., Optimal Bang-Bang Control with Quadratic Performance Index, J. Basic Eng.. 1964. 86, № 3, pp. 107-115.

261. Yu Chi Ho. Solution Space Approach to Optimal Control Problems. Paper № 60-JAC-ll.

262. Zachary D. H. Further Consideration of an Optimal Control Problem. Int. J. Control, 1S66. 4, № 3, pp. 281-296.

263. Zachary D. H. Finite Time Optimization of Bang-Bang Control Systems, Int. J. Control. 1966. 4, № 4. pp. 357-364.

264. Hiratsuka Sh., Ichikawa A. Optimal Control of Systems with Transportation Lags, IEEE Trans. Autom. Control, 1969, AC-14, pp. 237-247.

265. Kyong S. H., Qyftopoulos E. P. A Direct Method for a Class of Optimal Control Problems, IEEE Trans. Autom. Control, 1968, AC-13, pp. 240- 245.

266. Kleinman D. L., Athanas M. Design of Suboptimal Linear Time-Varying System, IEEE Trans. Autom. Control, 1968, AC-13, pp. 150-159.

267. Anderson B. D. O., Moore J. B. Linear System Optimisation with Prescribed Degree of Stability, Proc.IEE. 1966, 116, pp. 2083-2087.

268. Luh J. Y. S., ShafranJ. S. Construction of the Minimal Time Control for Processes with Bounded Control Amplitudes and Rates, IEEE Trans. Autom. Control, 1969, AC-14, pp. 150-164.

269. Aoki M., Li M. T. Optimal Discrete-Time Control System with Cost for Observation, IEEE Trans. Autom. Control, 1969, AC-14, pp. 165-175.

270. Dyer P., McReynolds S. R. Optimization of Control Systems with Discontinuities and Terminal Constraints, IEEE Trans. Autom. Control, 1969, AC-14. pp. 223-229.

271. Polak E., Deparis M. An Algorithm for Minimum Energy Control, IEEE Trans. Autom. Control. 1969. AC-14, pp. 367-377.

272. Franke D., Schieffer P., Weber W. Schnelligkeitsoptimale Regelung der Oberwalzenanstellung einer Blickstrasse, Regelungstechnik, 1969, 17, pp. 197-244.

273. Luh J. Y. S.. Lukas M. P. Suboptimal Closed-Loop Controller Design for Minimum Probability of Inequality Costrains Violation, IEEE Trans. Autom. Control, 1969. AC-14, pp. 449-457.

274. MacFalane A. G. J. Dual-System Methods in Dynamical Analysis, Proc. lEE. 1969. 116, pp. 1453-1462.

275 Jacobson D. H., Gershwin S. В., Lele M. M. Computation of Optimal Singular Controls, IEEE Trans. Autom. Control, 1970, AC-15, pp. 67-73.

276. Jacobson D. H. On Condhions of Optimality for Singular Control Problems. IEEE Trans. Autom. Control. 1970, AC-15, pp. 109-110.

277. Klafter R. D. On the Solution of Time-Optimal Control Problems in the Presence of Quadratic Constraints, IEEE Trans. Autom. Control. 1970, AC-15, pp. 114-115.

278 Sobral M., Boffi L. V. On the Optimization of a Certain Class of Nonlinear Systems. IEEE Trans. Autom. Control. 1970, AC-15, pp. 111-112.

279 Davison E. J., Seugnet J. M. A minimum-Time Intercept Problem, IEEE Trans. Autom. Control, 1970, AC-15, pp. 116-118.

280 Westdal J. A. S., Lehn W. H, Time Optimal Control of Linear Systems with Delay, Int. J. Control. 1970, 11, pp. 599-610.

281 Reeve P. J. Optimal Control for Systems which Include Pure Delays, Int.

J. Control. 1970. 11, pp. 659-681.

282. Luh J. Y. S., Shafran J. S. An Approximate Minimal Time Closed-Loop Controller for Processes with Bounded Control Amplitudes and Rates. IEEE Trans. Autom. Control, 1970, AC-15, pp. 185-194.

283 Alam M. A. A Constrained Optimal Control of Nonlinear Systems, IEEE

Trans. Autom. Control. 1970, AC-15. pp. 228-232.

284 Davies M. J. A Propsrty of the Switching Curve for Certain Systems, Int. J. Control. 1970. 12, pp. 457-463.

285. Kirby В. J., Cook V/. Pseudo-Convexity and Quasi-Concavity in Optimal Discrete-Time Control Systems., Int. J. Control, 1971. 13, pp. 189-198.

286. Fuller A. T. Suboptimal Nonlinear Controllers for Relay and Saturating Control Systems. Int. J. Control, 1971. 13, 1971. pp. 401-428.

2. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ

В 50-х годах американский математик Р. Беллман и его сотрудники разработали новый подход к решению вариационных задач [8*-11*, 13*-15*. 17*, 18*, 21*, 23*, 34*]. Предложенный ими метод динамического программирования часто применяется для анализа и синтеза систем оптимального управления.

2.1. ОСНОВНЫЕ ПРИНЦИПЫ

Рассмотрим нестационарное векторное дифференциальное уравнение .

x = f(x, U, 0. (2.1-1)

где векторы х и f имеют размерность п, а размерность вектора U равна г. Вектор управления и удовлетворяет ограничениям

uef/, (2.1-2)

где L-множество допустимых значений. Критерий оптимальности состоит в минимизации функционала стоимости

I {MMt), t)dt, (2.1-3)

о

в котором подынтегральное выражение Р (х(0, (0.0 определяет функцию цели, а верхний предел интегрирования Г>0 может быть фиксированным или переменным. Начнем со случая, когда конечный момент времени Т равен некоторой постоянной величине.

Введем новую переменную

ХоЦ)= JMxit), u(t), t)dt. . (2.1-4)

Очевидно, что задача минимизации функционала / эквивалентна минимизации состояния Хо{Т) системы, уравнения которой можно записать в виде

l=l{x{t), u{t), t)dt, (2.1-5)

где = [хо, xl и f г = [/о, [tj векторы размерности п + 1, в то время как размерность вектора и по-прежнему равна г.

Вектор начальных условий х' (0) = [0, хТ(0)].

Отметим, что выбор целевой функции /о=0 приводит к задаче об оптимальном быстродействии 7 = Гмин.

Ограничимся, кроме того, рассмотрением автономных систем. Это не приводит к потери общности: всегда можно, как было показано в разд. 1.1-1, ввести новую переменную Xn+i(t) = t и еще одно дифференциальное уравнение Xn+i(t) = l с начальным условием a: +i(0)=0. В этом случае вместо времени рассматривается переменная состояния Xn+i и задача сводится к рассмотрению автономной системы

x{t) = f{x{t), u{t)), (2.1-6)

вместо системы (2.1-1).

Принцип оптимальности. Динамическое программирование основано на принципе оптимальности, впервые сформулированном Беллманом. Рассмотрим оптимальную траекторию в п-мер-ном пространстве состояний (рис. 2.1-1). Положение движущейся точки в момент времени tf {0<f<T) обозначим через х (f). Эта точка делит траекторию на две части.

Принцип оптимальности утверждает, что отрезок оптимальной траектории от точки х (Г) до точки х(Т) также является оптимальной траекторией.

Это означает, что для начального состояния х (f) та часть траектории, которая соответствует переходу из точки х (f) в точку х(Т), является оптимальной независимо от предыстории системы, т. е. от того, каким образом система достигла состояния xo(f). Допустим, что это не так, т. е. найдется траектория (например, отмеченная штрихами на рис. 2.1-1), вдоль которой значение функционала меньше. Полное значение функционала / равно сумме его значений, вычисленных по двум отрезкам траектории. Отсюда следует, что можно построить траекторию, которая будет лучше исходной. Для этого надо выбрать вектор допустимого управления так, чтобы начальный участок траектории остался прежним, а ее второй участок совпал с штриховой кривой. Таким образом, мы пришли к противоречию с гипотезой* оптимальности первоначальной траектории. Отсюда следует, что нельзя улучшить заключительный участок траектории и, следовательно, этот отрезок оптимальной траектории в свою очередь также является оптимальным.

Принцип оптимальности Беллмана [1-8] дает достаточно общее необходимое условие оптимальности, которое можно применять как для непрерывных, так и для дискретных систем.

Несмотря на кажущуюся простоту этого принципа, из него можно вывести совсем нетривиальные необходимые условия оптимальности траектории.

Принцип оптимальности можно также сформулировать следующим образом: оптимальная стратегия не зависит от предыстории системы, а определяется только начальным условием и конечной целью.

- Отличительная особенность метода, использующего принцип оптимальности, состоит в том, что отрезки оптимальной траектории определяются в обратной последовательности, начиная с предписанного конечного или целевого состояния х(Т). Подчеркнем еще раз, что в соответствии с принципом оптимальности участок, примыкающий в конечной точке оптимальной траектории, в свою очередь является оптимальным, иначе говоря, оптимальность этого участка всегда следует из оптимальности всей траектории.

При делении траектории на несколько отрезков можно, двигаясь в обратном направлении, убедиться в оптимальности отрезка траектории, прилегающего к последнему, а затем - в оптимальности всех предшествующих отрезков. Оптимальность отдельных участков траектории зависит от оптимальности всей траектории. Обратное утверждение не имеет места, т. е. оптимальность всей траектории не следует из оптимальности отдельных участков.

Дискретная форма динамического программирования. Рассуждения Беллмана поясним для случая дифференциального уравнения (2.1-6) и минимизируемого функционала стоимости

Рис. 2.1-1. Оптимальная траектория в /1-мерном пространстве состояний (п=3).

/ = ср(х(Г))+ 1/о(Х, U)dt. О

(2.1-7)

Для простоты рассмотрим случай фиксированного времени Т; допустим также, что ф(х(0))=0. Заметим, что функция ф не зависит от вектора управления иС). Таким образом, значение ф(х(Г)) зависит только от конечного состояния х(Г) и не зависит от того, каким образом система достигла этого состояния.

Для начала представим эту задачу в дискретной форме. В такой постановке легче проиллюстрировать метод решения задачи, кроме того, аналогичный подход используется при применении вычислительного устройства.

Разделим интервал (О, Т) на М подынтервалов одной и той же длительности Д/. Рассмотрим векторные величины X =х(тДО и и, = и(тДО, определенные для моментов времени тД/(т = 0, 1, М-\, М\ MLt=T).

Исходное дифференциальное уравнение аппроксимируется разностным уравнением

±p f(x uj. (2.1-8)

Имеет место приближенное равенство

x, -n = x + f(x , и„)ДД (2.1-9)

Функционал стоимости (2.1-7) аппроксимируется суммой и может быть записан в следующем виде:

= Т Ы + J/o (х^, U J АД (2.1-10)

Задача состоит в том, чтобы определить векторы управления Uo, Ui, ... , u j при ограничении uet/ таким образом, чтобы минимизировать эту сумму, причем поведение системы описывается разностным уравнением (2.1-9) с начальным условием х(0).

В соответствии с принципом оптимальности приступим к решению задачи, отправляясь от конечного состояния процесса при t=T, и будем двигаться в обратном направлении.Допустим, что вектор Um(m=0, 1, ..., М - 2) уже каким-то образом выбран и теперь только требуется для данного состояния Xm-i определить вектор Um-i. Согласно принципу оптимальности, Um-i не зависит от предыстории системы и определяется состоянием Xflf-i и целью управления Обозначим через 1м-\ последнюю частную сумму полной суммы /:

= <Р(Хж) +/о(Хж-1. А^- (2.1-11)

Исходя из приближенного равенства (2.1-9), найдем, что вектор состояния

= + f (Хж-1. ж-О (2-1-12)

также зависит от вектора управления Мм-и Определим допустимое значение uj i е [/ вектора управления u j, минимизирующего сумму 1м-1 и удовлетворяющего уравнению (2.1-12). Обозначим через S-i минимальное значение выражения /м-i; Очевидно, что 5 j зависит от состояния м-\= м-\- Согласно принципу оптимальности, заключительная часть рассматривае-

мой траектории является оптимальной и начинается из точки х^ 1. Из соотношений (2.1-11) и (2.1-12) получим, что

Sm-i{%-i)= min min !<?(х^)+/о(х , р иж-1)Д^} =

= min {<?(x i + ж-О 0 +/о(х ж-1 ж-О'Д^).

Ж-16 f

(2.1-13)

Рассмотрим теперь отрезок траектории, предшествующий последнему участку. Из выражений (2.1-10) и (2.1-11) найдем, что последние две частные суммы определяются равенством

= Ж-1 +/о (Хж 2 M-i)

= ?(Хж)+/о(х,и 1, и^ 1)Д^+/о(х^, 2. иж-2)Д^- (2.1-14)

Будем считать, что состояние х^/ 2 задано, тогда в соответствии с принципом оптимальности рассматриваемый участок траектории также оптимален и, следовательно, начинается из точки x j 2. Из принципа оптимальности вытекает, что управление определяется только состоянием x)j 2 и целью управления, состоящей в минимизации функционала /м-2- Найдем минимум / 2Для векторов управления и^ и и° . Минимум /г-рТ- е величина ix% i) для произвольного состояния x°j j и

оптимального управления u5 уже найден. Следовательно, для

отыскания минимума /м-2 можно воспользоваться следующим условием:

л1-2(х ж-2)= min /ж-2= min {5 i(xO, i)-f Ож-1 е

+ /о(Х ж-2. ж-2) =

= min 5 1 (х , , +/(х5;, 2, и^ 2) +

М-2 6 и

+ /о(х ж-2.и°ж-2)А/}. (2-1-15)

в результате минимизации можно определить оптимальный вектор u j 2 и минимальное значение 5, 2 (хО 2) через х^-г-Затем процедура повторяется для следующего участка траектории, который предшествует рассмотренному. Общая рекуррентная формула для т-го от конца отрезка траектории имеет вид

Ж-ш(Хж-т)= min ( -02+ ,п 1 1ДЧ

+ *(V . м.и- .)ДО +/o(xV, %- .)д^}.

Определяя минимумы, найдем оптимальный вектор В результате последовательного применения этой формулы для определения величин 8м~т (т=1, 2, ..., М) можно найти вектор оптимального управления и° для первого участка траектории и таким образом определить величину 5о(х ), равную минимуму /.

К сожалению, только в простейших случаях описанная выше процедура может быть выполнена аналитически; для этого необходимо, чтобы аналитические зависимости 5м-т ) м-т можно было выразить в замкнутой форме. Однако в общем случае это требование не выполняется, поэтому процедуру динамического программирования можно классифицировать, как следует из самого названия, в лучшем случае в качестве метода для ручных расчетов или в более сложных случаях для вычислений на ЭВМ. Тем не менее метод динамического программирования имеет явное преимущество по сравнению, например, с прямым методом минимизации функционала при наличии ограничений. Этот функционал, как следует из выражения (2.1-10), является сложной функцией многих переменных:

/ = /(Хо, Xi, Хм; Uo, Ui, liM-i). Метод динамического программирования проще известных численных методов минимизации функции многих переменных; к тому же традиционные методы дифференцирования оказываются бесполезными в том случае, когда минимум достигается на границе области управления U.

Метод динамического программирования позволяет свести задачу минимизации сложной скалярной функции нескольких аргументов к минимизации последовательности скалярных функций от одного векторного аргумента. Несмотря на это, в общем случае даже алгоритм динамического программирования приводит к очень громоздким процедурам отыскания решения. При этом на каждом шаге работы алгоритма необходимо вычислить и запомнить численные значения 5ж т Л-т) м-, +Л^м-т+1) скалярных функций векторного аргумента (т. е. скалярных функций многих переменных). Их хранение в памяти машины требует большой емкости запоминающего устройства. Некоторые подходы, позволяющие преодолеть эти трудности, впервые были предложены в работе Беллмана и Дрейфуса [18]. Наконец, следует отметить, что в литературе основное уравнение динамического программирования часто используют для значения А/=1. Таким образом, прираш,сние можно формально исключить из этого уравнения.

Динамическое программирование для систем, подверженных возмущениям. Динамическое программирование можно распро-

странить на случай анализа оптимальных систем, находящихся под действием случайных возмущений. Допустим, что на систему управления действует вектор возмущений z с компонентами Zi. Тогда вместо выражения (2.1-9) будем иметь равенство

= х„, + f (х, , и„, z, ) Д^, (2.1-17)

в котором Zm (т=0, 1, . .., М-1)-последовательные значения вектора возмущений. Поскольку в этом случае векторная величина х™ и первоначальный функционал зависят от случайных переменных, примем в качестве нового критерия минимизации математическое ожидание суммы вида (2.1-10):

/ = М <.(Хж)-Ь IjMXm, u, , z)U\. (2.1-18)

где предполагается, что целевая функция также зависит от возмущений.

Пусть плотность вероятности p{zm,) известна. Исходя из принципа динамического программирования, получим соотношение

М~1 (Хж-1 М-т) ~

= min М (xVi -Ь f (хж-1, иж-ь Zm-i) А/) + ж-1 eu

+ /o(xVi. ж-Р ж-О Д^} =

= min J... J KxVi+fC-i.-i. 2ж-1)Д0 +

Ж-1 е -со -со

+ /о(х5-Р ж-!. ж-О t]P{m-)dz], , ... с1г , (2.1-19)

в правой части которого необходимо произвести многократное интегрирование по п компонентам вектора z-[г*, .. ., г ] и zi= M{zm-i}. Двигаясь в обратном направлении, получим рекуррентную формулу динамического программирования

5и-, {Al- М-т )= min М {S , (Х^ -ЬР M-,n+l) +

+ /o(xV . = min

+ /о(х ж-., и^ , z J Д() Р{г^ )с1г\, ...с1г'1, . (2.1-20)

Возможны дальнейшие теоретические обобщения полученных результатов; так, например, можно считать, что ПАОтнодть верО

ятности p(Zm) неизвестна и определяется по результатам конечного числа наблюдений [19].

Динамическое программирование для непрерывных систем. Векторное дифференциальное уравнение автономного нелинейного управляемого объекта в этом случае имеет вид

X = f(X, U, t).

(2.1-21)

Критерий оптимальности состоит в минимизации функционала стоимости

г

= J/o(x it), u{t), t)dt.

(2.1-22)

Допустим, что х (О - оптимальная траектория с начальным состоянием х(0) и конечным состоянием х (Г) (рис. 2.1-2). Обозначим через 5(х'(0), 0) минимум функционала /. Из принципа оптимальности следует, что отрезок траектории с концами x{t) и х(Г), отвечающий решению уравнения (2.1-21), также оптимален. Следовательно, минимальное значение порождаемого им функционала равно

5(х (0. 0 =

т

= minj/o(x0(&), u(&), b)d.

uqU t

(2.1-23)

Это соотношение называется функциональным уравнением Беллмана. Для достаточно малого интервала длительности

и момента времени t = t-\- Д^ минимальное значение функционала, вычисленное по отрезку оптимальной траектории с началом в точке \ (t) = х° {t + t\t) и с конечным состоянием х(Г), определяется формулой

т

S{x4t), t)=mm I/o(x<>(&), u(&), b)db. (2.1-24)

В левой части равенства (2.1-24) аргументы x(t) и t служат для обозначения начального состояния на рассматриваемом участке траектории. По аналогии с рекуррентной формулой (2.1-16) дискретного динамического программирования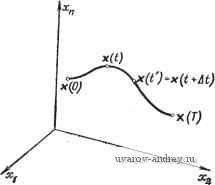

Рис. 2.1-2, Оптимальная траектория.

[заменой 5 ,(х , , ) на 8(хО(П П (х% ,+,) на

5(х (П, ) и/о(х , , иж-, ) на /о(х (0, v4i),i)U] или из сравнения интегралов (2.1-23) и (2.1-24) получим, что

5 (X (О, t) = min { f/о (x ( ), u (&), &) db +

+/o(x (0. u(0. /)Д^} + 01(ДО, (2.1-25)

5(xO(0, )= min {5(x0(O. 0+/o(x (0. W. t)M} + OiiM),

(2.1-26)

где Oi (Д^)-остаточный член выше первого порядка малости от Д^:

lim-ii = 0. (2.1-27)

В силу конечности интервала в правых частях этих равенств необходимо учитывать слагаемое Oi (At). Из разложения в ряд Тэйлора получим, что

X [п = x{t + M) = x{t) + x (t) Lt + 02 (Д^) =

= X (О + * (X {t), u (О, t) М -V 02 (Д^), (2.1-28)

где 02(Д^-остаточный член выше первого порядка малости от Д^. (Заметим, что последнее выражение соответствует разностному уравнению (2.1-9).) Подставляя выражение X () в формулу S{x{t), t) и разлагая в ряд Тэйлора при условии, что существуют частные производные dS/dXi {i=l, 2, и) и dSjdi, получим

S (X (Г), п = Six(t + U), + Д/) =

= 5 (X (/) + f (X (t), u (t), t) Ц -V 02 (Д/), -Ь Д^) -

п

= 5(x(), )+2-%Л(х(4 uW. t)M +

f (y ) Д^ + Оз(Д0. (2.1-29)

где Оз(Д^) - остаточный член выше первого порядка малости от Д^. Сумма второго и третьего членов в правой части этой формулы равна полной производной dSjdt. Вводя вектор-столбец

dS 6S dS

grad5=f- =

dx [ dxj дх дх