В данной части показано, что системы управления, к которым предъявляются специфические требования, например релейные системы или системы с ограничениями на переменные, минимизирующие время (расход топлива или энергии), можно реализовать, используя нелинейные характеристики. Подобные задачи или не могут быть решены вообще с помощью линейных систем, или решаются только в исключительных случаях с помощью специальных приемов. Теория управления, так же как любая другая техническая наука, имеет дело главным образом со стационарными линейными системами. Это могло бы создать впечатление, что стационарные линейные системы составляют общий случай, а нестационарные или нелинейные системы - исключение. Однако на практике физические системы в основном нелинейны, причем параметры в той или иной степени зависят от времени [3]. В каждой физической системе рано или поздно устанавливаются некоторые ограничения либо при убывающих колебаниях переменных (например, границы чувствительности), либо при возрастающих (явление насыщения и т. п.). Фактор времени обнаруживается в явлениях старения и усталости. Распространенность стационарных линейных моделей можно объяснить тем, что их довольно простое математическое описание приводит к очень общим теоремам. Анализ, а тем более синтез нестационарных и, в частности, нелинейных систем, напротив, чрезвычайно сложен и труден. Их описание приводит к небольшому числу общих теорем [1, 2]. Поэтому обычно предпринимаются попытки заменить, если возможно, нестационарную или нелинейную систему линейной моделью и исследовать последнюю. При этом, однако, не следует забывать, что линейная система представляет собой некоторую степень математической абстракции, которая не встречается в чистом виде в реальном физическом мире. Все это говорит о чрезвычайной важности нелинейных и нестационарных систем [1*, 3*. 7*, 12*, 26*, 32*, 49*-51*, 55*, 58*, 62*, 65*. 66*, 68*, 72*. 80*. 82*,

84*. 86*, 89*, 98*, 99*, 101*, 106*, 108*-110*, 133*, 138*, 141*, 144*, 147, 1491 .

1.2. ОСНОВНЫЕ УРАВНЕНИЯ

Каждый элемент, устройство или часть стационарной линейной системы описывается линейным алгебраическим или дифференциальным уравнением с постоянными коэффициентами (в случае нескольких переменных - совместной системой алгебраических или дифференциальных уравнений).

Таким образом, система, показанная на рис. 1.2-1, линейна, если связь входной переменной u(t) с выходной y(t) может быть записана в виде

у(0 = /С (4 (1.2-1)

где К - постоянный коэффициент усиления. Аналогично система (или элемент) линейна, если связь можно выразить, например, с помощью дифференциального уравнения

dy{t)

Рис. 1.2-1. Блок-схема преобразователя или системы управления.

+ 1

-a,nt) = u{t), (1.2-2)

где an, ... 1 о - постоянные коэффициенты.

Элемент с временными задержками также будет линейным, если, например, справа записать u(t - Тв). Известно, что линейные системы удобно изучать с помощью преобразования Лапласа, которое преобразует дифференциальное уравнение в алгебраическое с комплексной переменной.

Если коэффициент усиления К или любой коэффициент йп, ..., Go зависит от времени, то элемент (устройство или часть системы) является нестационарным (неавтономным). В этом случае то же самое можно сказать о всей системе. Например, система, показанная на рис. 1.2-1, будет нестационарна, если

y{t)K{t)a{t) (1.2-3)

(О . . + 1 (О+ 0 (О У (О = (t). (1.2-4)

или

Отметим, что рассмотренные выше нестационарные системы являются линейными, т. е. к ним применим принцип суперпозиции. Например, если входным переменным Ui(t) и ЫгГО соответ-

* Звездочками обозначены ссылки на литературу, помещенную в конце книги. -Прим. ред.

ствуют выходные переменные y\(t) и УгГО. то и для нестационарной системы входной переменной Ui(t) + U2(t) будет соответствовать выходная переменная {/ifO+TO- Это легко проверить, например, подстановкой в дифференциальное уравнение (1.2-4)-

Нестационарные системы значительно труднее анализировать, чем стационарные. Преобразование Лапласа не приводит к таким простым результатам, как в случае постоянных параметров, так как преобразование Лапласа от произведения функций времени будет равно интегралу свертки по комплексной переменной. В общем случае решение уравнений с переменными параметрами или дифференциальных уравнений выполняется во временной области, и методы решения их часто напоминают методы решения нелинейных или дифференциальных уравнений.

Наконец, если дифференциальное уравнение, описывающее поведение системы, нельзя преобразовать к виду (1.2-4), то система нелинейна. Например, если в исследуемых алгебраических или дифференциальных уравнениях зависимая переменная (например, выходная) или ее производная некоторого порядка присутствует не только в линейной форме, но также в произведении с другими переменными или в любой целой или дробной степени, то эти уравнения нелинейны [3]. Естественно, когда зависимая переменная допускает форму степенного ряда или аналитически замкнутое выражение от него, алгебраическое или дифференциальное уравнение опять будет нелинейным. Если, например, в системе, показанной на рис. 1.2-1, связь входных переменных с выходными имеет вид

[y(i)] = Kuii) (1.2-5)

или

\y{i)V = Kait), (1.2-6)

где пФ\-целое число, то система нелинейна. Аналогично система нелинейна, если она описывается, например, дифференциальным уравнением вида

+ sin у (О =Ku(i). (1.2-7)

Решить нелинейные уравнения выше первого порядка обычно очень трудно, и каждый тип нелинейного или дифференциального уравнения необходимо исследовать отдельно.

Следует добавить также, что нелинейную зависимость часто нельзя выразить в математическом виде или эта зависимость справедлива только приближенно. В таких случаях связь выражают графически. Немало подобных случаев встречается в инженерной практике; графики намагничивания, характеристики электронных ламп, транзисторов, волноводов и т. д.

Отметим, что принцип суперпозиции неприменим к нелинейным системам. Следовательно, обычные определения стационарной и переходной составляющих здесь не имеют смысла. Сигналы нельзя разложить на составляющие и рассматривать их отдельно. В нелинейной системе всегда рассматривается весь сигнал [3, 8]-

Итак, система нелинейна, если ее работа описывается нелинейным уравнением (или системой уравнений), дифференциальным уравнением (или системой) или нелинейным графиком. В нелинейных системах принцип суперпозиции перестает быть справедливым-

1.3. УРАВНЕНИЯ СОСТОЯНИЯ

Поведение системы (или преобразователя) можно описать также уравнениями состояния, или фазовыми уравнениями [33*, 36*, 37*, 135*, 142*, 145*, 151*]- При этом с точки зрения теории нет различий между одномерными и многомерными системами [3-7].

Уравнения состояния неавтономных нелинейных систем имеют вид

X = f(X, U, t), . , ,

y = g(x. u, t), -

где x=xC/)-вектор состояния (матрица-столбец порядка nXl); u = u(t) - вектор управления, состоящий из входных переменных (матрица-столбец порядка гХ1); y=y(i)-выходной вектор, составленный из отдельных выходных переменных (матрица-столбец порядка Xl), и -время. Первое уравнение является векторным дифференциальным уравнением первого порядка, а второе - алгебраическим векторным уравнением. В общем случае допускается, что пХ 1-мерный вектор-столбец f и 9Х 1-мерный вектор-столбец g выражают нелинейные зависимости. Отметим, что при рассмотрении уравнений состояния объекта управления выходной вектор у совпадает с вектором управляемых переменных.

Запишем векторные уравнения (1.3-1) в виде

Xi - fiiit 5 Xfii u-i, ... , tif f) i}- 1) 2, ..., ti)

(совместная система дифференциальных уравнений),

yjgji-i ... , x ; lii, ... , и/, t) (У= 1, 2.....q)

(совместная система алгебраических уравнений).

Уравнения состояния автономной (некоторые авторы называют систему автономной только тогда, когда она не возбуж-

дена) нелинейной системы (или преобразователя) имеют вид

x = f(x, U).

y = g(x,u). (1-3 2>

уравнения (1.3-1) и (1.3-2) можно использовать для линейных как неавтономных, так и автономных элементов (или систем). Для линейных систем, однако, эти уравнения обычно записываются Б другой форме. Уравнения состояния неавтономного линейного элемента (или системы) имеют вид

X = А (О X + В (О U, y = C(0x + D(0u,

а для автономного линейного элемента (или системы)

х = Ах + Ви, y = Cx + Du,

(1.3-3)

(1-3-4)

где А, В, С и D есть матрицы порядка пХп, пХг, пХп и дХг соответственно с постоянными элементами. Если некоторые элементы зависят от времени, матрицы обозначаются через А(), В(), С() и D{t), символы у, х, и обозначают зависящие от времени векторы у(), х() и и(). Заметим, что один и тот же элемент (или система) может иметь несколько различных векторов состояния, т. е. уравнения состояния и векторы состояния не единственны.

Если отдельные компоненты вектора состояния х (отдельные элементы матрицы-столбца х) связаны между собой дифференциальными уравнениями типа

Xi+i=--xi = xi (г = 1, 2, /г-1), (1.3-5)

то вектор X называется фазовым вектором, а его компоненты - фазовыми переменными, или фазовыми координатами. Следовательно, фазовый вектор является специфическим вектором состояния.

Нелинейный или нестационарный характер элемента (или системы) обнаруживается, таким образом, в его уравнениях состояния так же, как в его дифференциальном уравнении. В этом отношении дифференциальное уравнение и уравнения состояния эквивалентны.

Определение уравнений состояния и фазовых уравнений по передаточным функциям линейного элемента (или системы), и наоборот, рассматривается в приложении (часть V). Приведем несколько простых примеров.

Пример 1. Найдем фазовые уравнения преобразователя, заданного дифференциальным уравнением (1.2-4).

Вводя соотношение u{t) = u и фазовые переменные Xi{i = = 1, 2, ... , п) ]л и:пользуя уравнения х, = у, = у, ... ,х„ = = у( -Ч, получим фазовые уравнения

X] = х^,

Х2 = -3 ,

(О 1 + ... + а„-1 (О . 1 + и.

у = Xi,

где

А (0 =

х = Ао(/)х + Ьо() и.

у = СоХ.

О О

1 О

О

с?(0 = [1. О, О, 0] = cj.

Таким образом, матрица (t) сводится к матрице-столбцу (вектору-столбцу) bo(t), а матрица СГО-к матрице-строке (вектору-строке) Сд. Здесь и ниже верхний индекс Т обозначает транспонирование.

Вводя произвольную невырожденную матрицу Т, т. е. преобразование

X = Тх,

где X-фазовый вектор, х'-вектор состояния, получим уравнения состояния

х' = А()х' + b(Oii,

где

А(0 = Т-1Ао(/)Т, Ь() = Т'%(4

с' () = с?Т.

пример 2. Нелинейное дифференциальное уравнение (1.2-7) принимает вид уравнения состояния

л: = - sin X + Ки,

В данном случае функция f(x, и) равна сумме нелинейной функции -smx и линейной функции Ки, функция g(x, и) равна g(x)=x.

Задача. Показать, что в уравнениях состояния преобразователя, который описывается дифференциальным уравнением с постоянными коэффициентами

п т

1=1 7 = 1

матрицы Ао и bo совпадают с матрицами из примера 1 (с постоянными коэффициентами) и

т 1

с = Со == - [aj) - аф, а„6 1 -

1.4. НЕКОТОРЫЕ СПЕЦИФИЧЕСКИЕ СВОЙСТВА НЕЛИНЕЙНЫХ СИСТЕМ

Нелинейные системы отличаются от обычных линейных систем во многих отношениях [3, 8-13, 18].

В линейных системах с постоянными параметрами вид и поведение выходной переменной не зависят от ве/шчины входной переменной, так же как выходная переменная в установившемся режиме не зависит от начальных условий. В нелинейных системах поведение выходной переменной зависит от величины входной, а также от начальных условий. На рис. 1.4-1 приведены для сравнения выходные величины. Очевидно, что увеличение импульса на входе (U) не меняет формы выходной реакции линейной системы (пунктирная линия), в то время как форма выходной реакции нелинейной системы (сплошная линия), частота колебаний и время перерегулирования сильно меняются.

Аналогичные соображения справедливы и для устойчивости системы. В линейных системах устойчивость является характеристикой системы, не зависящей от величины входной переменной и начальных условий. В нелинейных же системах устойчивость может зависеть от величины входной переменной и (или)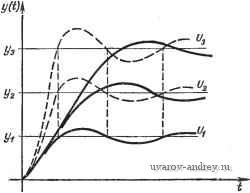

Рис. 1,4-1. Сравнение выходных величин в линейной и нелинейной си-

стемах-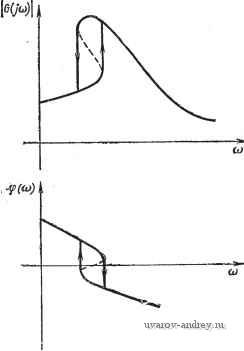

Рис, 1,4-2, Частотные характеристики нелинейной системы.

начальных условий: например, система может быть устойчивой при низкочастотном входном сигнале и становится неустойчивой при высокочастотном, и наоборот.

Понятие статической точности (установившейся ошибки) также должно быть пересмотрено, так как, например, в случае сухого кулонова трения система может иметь несколько точек равновесия в стационарных условиях [17].

В линейных системах с постоянными параметрами в квазистационарном режиме выходной сигнал имеет составляющие с частотой, равной частоте входного сигнала. В нелинейных же системах могут возникать высшие гармоники и, что самое удивительное, субгармоники [9-12].

В автономных линейных системах на определенной частоте возникает резонанс. Увеличение или уменьшение частоты сопровождается непрерывным изменением амплитуды и фазы. В нелинейных же системах, как показано на рис. 1.4-2, вблизи резонансной частоты могут происходить скачкообразные изменения амплитуды и фазы (пунктирная кривая, соответствующая незатухающим колебаниям, не может, конечно, иметь место в стационарных условиях). Следует отметить, что амплитудные и фазовые диаграммы зависят также от величины входной (синусоидальной) переменной [18].

В нелинейных системах могут возникать так называемые предельные циклы: независимо от величины входной переменной или начальных условий на выходе системы в отношении внешних воздействий возбуждаются колебания, которые в общем случае не являются гармоническими [8, 14-16].

Хотя этот перечень специфических свойств нелинейных систем и далек от полноты, он показывает, насколько сложнее нелинейные системы по сравнению с линейными. Указанные явления нельзя даже приближенно описать с помощью линейных моделей.

1.5. КЛАССИФИКАЦИЯ НЕЛИНЕЙНОСТЕЙ

На Основе статических характеристик нелинейности можно разделить на существенные (или несомненные) и устранимые (или нежелательные) [48*-50*, ПО*, 111*]. Существенная нелинейность обязательна для основной работы системы, например в контактной системе управления, релейном сервомеханизме, нелинейном компенсаторе и т. д. Часто такую нелинейность называют преднамеренной. Устранимая нелинейность не является преднамеренной. В первом приближении ее устранение не ведет к серьезным последствиям, и работу системы можно приближенно оценить, не принимая ее во внимание. Такого типа нелинейности называют также паразитными или^сдрадацли.

при более точном анализе, конечно, необходимо учесть также и этот тип нелинейности.

На рис. 1.5-1 приведена блок-схема простого сервомеханизма, где нежелательные нелинейности включают насыщение предусилителя и усилителя мощности, полосу нечувствительности (границы чувствительности усилителей, порог серводвигателя (из-за кулонова трения) 17], гистерезисы кривых намагничивания двигателя и их насыщения, нелинейности, присущие двигателю, мертвый ход зубчатой передачи и гранулирован-ность потенциометра обратной связи.

На основе статических характеристик нелинейности можно, кроме того, разделить на однозначные и многозначные. Характеристика идеального реле или выпрямителя, например, представляет собой однозначную нелинейность или, другими слова-

r(t)

ю

Компенсатор

- Усилител

передача

y(i).c(t)

6 цепи шной сВлзи

Рис. 1.5-1. Блок-схема нелинейного сервомеханизма или системы управления.

ми, нелинейность без памяти, в то время как характеристика действительного реле представляет собой многозначную нелинейность.

Нелинейности можно разбить также на разрывные и непрерывные. Например, кулоново трение описывается разрывной функцией [17, в то время как кривая намагничивания непрерывна. В свою очередь непрерывные нелинейности распадаются на группы с характеристическими функциями, которые либо всюду дифференцируемы, либо имеют отдельные точки излома. Примерами последнего типа нелинейностей служат кривые порогового типа, кривые с зоной нечувствительности и с мертвой зоной.

Нелинейности можно также классифицировать по их динамическому поведению [47*-50*, 110*, 111*]. Медленно меняющиеся нелинейности описываются функциями, которые меняются медленнее, чем сигналы. Медленно меняющиеся нелинейности имеют место при старении электронных ламп, усталости пружины, восстановлении активности катализатора и т. д.

Быстро меняющиеся нелинейности описываются функциями, изменения которых сравнимы по порядку с изменениями сигналов. Примерами быстро меняющейся нелинейности служат за-