также к изменению привычных взглядов на постановку и проведение самого эксперимента. Это находит свое отражение в так называемой концепции рандомизации, используемой при планировании экспериментов. Суть этой концепции состоит в том, чтобы обеспечить случайность действия различных факторов, т. е. план эксперимента составляется таким образом, чтобы все воздействующие факторы оказывали случайное влияние на изучаемое явление. Рандомизация эксперимента стала одним из основных приемов и одной из важнейших предпосылок при планировании экспериментов.

Целесообразность использования рандомизированных планов обусловлена тем, что даже систематически действующие факторы, которые трудно учесть и контролировать, могут быть изучены (их влияние может быть выявлено) статистическими методами, составляющими раздел математической статистики - дисперсионный анализ.

Основную цель дисперсионного анализа поясним на простом примере одно-факторного анализа, когда проверяется действие только одного фактора. Пусть, например, одна и та же величина измеряется т однотипными измерительными п-р.1борами и требуется установить, можно ли считать систематические погрешности этих приборов одинаковыми. Другими словами, требуется проверить влияние одиого фактора - прибора - на погрешность результатов измерений. Выполним с помощью каждого прибора серию из п измерений. Всего получим пт результатов измерений гц, где /-номер прибора (/=!,..., т); т - количество приборов; i - номер измерений (t=I,..., п).

Таблица 23.1. Результаты эксперимента

При эксперименте будут получены следующие результаты измерений (табл. 23.1).

Оценка дисперсии результатов измерений (предполагается, что все результа ты представляют собой выборку из одной генеральной совокупности):

Оценка лисперснй, харамеризующай рассенние средних результатов измерения каждого прибора,

ш

В этой формуле Z -среднее арифметическое всех пт измерений.

Проверим теперь нулевую гипотезу, согласно которой центры рассеяния показаний каждого из приборов совпадают (т. е. гипотезу о равенстве систематических погрешностей приборов). Если нулевая гипотеза верна, то расхождение между £ *(Zij) и D*{z}) несущественно, если же обнаружится существенное расхождение между дисперсиями, то с большой вероятностью можио считать, что систематические погрешности приборов различны.

Идеи рандомизации и изучения рассеяния используются при применении других методов статистического анализа - метода главных компонентов, факторного анализа, дискриминаитного анализа.

Не всегда возможно или целесообразно планировать заранее весь эксперимент. В этих случаях применяется стратегия последовательного эксперимента, заключающаяся в том, что планируется сначала некоторый этап (шаг) эксперимента, затем производится анализ полученных данных и по его результатам принимается решение о следующем этапе (планирование следующего шага), в том числе может быть принято решение и о прекращении эксперимента

Математическая статистика внесла в теорию эксперимента идею оптимального использования пространства независимых переменных, или, как ее часто называют, идею многофакторного эксперимента. Суть этой идеи состоит в том, что при планировании экспериментов, в которых необходимо учитывать влияние многих независимых переменных (факторов), экспериментатору предлагается ставить эксперимент так, чтобы изменять все факторы сразу, тогда как при традиционном планировании экспериментатор изучает влияние каждого фактора в отдельности, изменяя только его значения при фиксированных значениях остальных факторов. Оказывается, что такое многофакторное планирование является более эффективным, чем однофакторное, так как позволяет значительно уменьшить погрешности определения интересующих экспериментатора величин. Покажем это на примере линейного регрессионного анализа.

Пусть некоторая величина х линейно зависит от т факторов у\,..., ут. Уравнение регрессии будет иметь вид

X=bo + biyi+ . . . +ЬтУт,

где bo, bi, bm- коэффициенты регрессии, которые необходимо определить по экспериментальным данным.

Так как количество подлежащих определению коэффициентов регрессии на единицу больше количества факторов, то к /п действительным факторам необходимо добавить один \ {,т-\ 1)-й] фиктивный фактор. Будем считать, что значения каждого фактора могут находиться только на одном из двух уровней, которые условно будем обозначать -fl (верхний уровень) и -1 (нижний уровень). При однофакторном планировании (поочередное изменение только одного фактора)

Применение последовательного анализа при контроле рассматривается в гл. 13.

дисперсии oiteiiOK коэффищ'еитов регресспн будут равны о^.1Ь,]=о^т/2/г (а'л- дисперсия, характеризующая погрсппюсть эксперимента; и -число повторных измерений при изменении каждого фактора) и, очевидно, ие будут зависеть от общего числа факторов. Если же изменять все переменные одновременно, то оценка дисперсии каждого из коэффициентов регрессии будет вычисляться по всей совокупности (т--1)/г опытов, так что при некоторых условиях можно получить оценку а^[6,-] в т-[-1 раз меньшую, чем при однофакторном эксперименте.. Таким образом, при увеличении числа независимых переменных т, учитываемых в эксперименте, эффективность многофакторного эксперимента растет как m-j-1.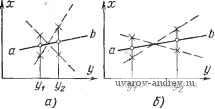

Рис. 23.1. К определению угла наклона прямой регрессии:

а - небольшое расстояние между точками и б - увеличенное по сравнению с предыдущим расстояние между точками у, и У2

Повышение эффективности многофакторного эксперимента (уменьшение дисперсий оценок коэффициентов регрессии) можно объяснить также следующим образом. При линейном регрессионном анализе коэффициенты регрессии при заданной погрешности эксперимента Ох определяются тем точнее, чем больше радиус обследуемой сферы, т. е. чем больше диапазон изменения независимых переменных. Например, в однофакторной задаче (рис. 23.1) чем больше расстояние между точками и j/s, в которых производится измерение, тем точнее оценивается коэффициент регрессии (угол наклона прямой регрессии аЬ). Многофакторные планы позволяют увеличивать радиус обследуемой сферы не только путем увеличения интервалов измеиеиия факторов (что не всегда возможно по условиям эксперимента), но и опираясь на свойства многофакторного пространства. Действительно, в одномерном пространстве радиус обследуемой сферы равен 1 (по-прежнему считаем, что переменные варьируются на уровнях +1), в двумерном пространстве этот радиус равен, очевидно, К2 (радиус окружности, описанной вокруг квадрата со стороной, равной 2), в случае т-мерного пространства радиус обследуемой сферы равен Vm.

Следует, однако, отметить, что не всякий многофакторный эксперимент позволяет уменьшить дисперсию оценок коэффициентов регрессии в m-f 1 раз. Этого можно достичь только путем соответствующего планирования многофакторных экспериментов (например, используя при линейной регрессии специальные планы, так называемые дробные реплики).

Планирование регрессионных экспериментов

Многочисленные задачи экспериментальных исследований на математическом языке могут быть сформулированы следующим образом: в результате эксперимента необходимо получить некоторое представление о зависимости интересующей исследователя величины х от нескольких независимых переменных (факторов) у1, ..., t/ft. Эти переменные (факторы) задают й-ыерное факторное про-страиство точек, ординатами которых являются значения уи ..., уи. Функцио-

нальная зависимость при фиксированном х

1=иУи .... Ук)

называется функцией отклика, или поверхностью отклика.

В общем случае аналитический вид функции отклика может быть неизвестным, поэтому приходится использовать полиномиальные модели, т. е. представ лять приближенно функцию отклика в виде полинома (такое представление, очевидно, можно использовать и тогда, когда вид функции отклика известен):

k k k

(=1 1=1 /=1

Результаты измерений величины g при различных значениях будут, очевидно, случайными величинами, так как измерения производятся с погрешностями (случайными). Поэтому значения у\, ..., ук будут определять величину g лишь в среднем, т. е. функция отклика будет определяться как математическое ожидание M{X\yi, Уь]- Задача состоит в том, чтобы по результатам эксперимента оценить коэффициенты Ро, Pi Таким образом, функция отклика есть

М[Х\уг. .... ун]Ш, УК. .ро, р. ...)

и представляет собой уравнение регрессии; эксперименты, целью которых является поиск оценок неизвестных параметров Ро, Pi - (коэффициентов регрессии) или неизвестной поверхности отклика, называются регрессионными; процедура поиска этих оценок называется регрессионным анализом.

В дальнейшем при изложении регрессионного анализа воспользуемся матрич-выми обозначениями. Итак, в некоторых точках й-мерного факторного пространства у1, ... yh производятся измерения величины X, являющейся функцией факторов уи ..., t/ft. Эти факторы образуют матрицу-столбец

Предположим, что выполнено п измерений, результаты которых можио представить матрицей-столбцом

причем эти измерения производились соответственно в точках с координатами

Уп, г/21.....Ум; г/12, (/22, . ., Уи; Ут, Win, , Укп- Будем считать также, что

все результаты измерений представляют собой независимые, нормально распределенные случайные величины X ..., Хп с дисперсиями а,2, ..., Ог?. Уравнение регрессии можно записать в следующем виде:

М [XIY\ = 5 (Г, V) = 1/гф (Г) = 2 V,Ф, (Г),

где

есть вектор оцениваемых параметров, составляющими которого являются все коэффициенты регрессии Ро, Рь ..., Рг, ..., Psj, ..., pii ...;

Ф(Г) =

<tm(Y)

- вектор известных функций [например, ф1(У) = 1, qi2(Y)-Y и т. д.]. Индекс т означает транспоиироваиие матрицы.

При определении оценок параметров V естественно потребовать, чтобы искомые оценки обладали по возможности такими свойствами, как состоятельность, несмещенность и эффективность. Кроме того, обычно ищут линейные оценки, т. е. такие, которые можно представить в виде

V*=,LA,

где V* - вектор оценок; L -матрица размерностью тХ -

Оценки, обладающие перечисленными выше свойствами, называют наилучшими линейными оценками, а для их определения можно воспользоваться следующей теоремой (см. [23.9]):

наилучшими линейными оценками для неизвестных параметров V являются

V*=T-X,

где Т - неособенная квадратная матрица порядка т с элементами

Тр, = 2 /¥р(5/)¥ч(>/)р. 9=1. 2, ..../п;

X - матрица-столбец с элементами

cui=I/ai=, 1=1, 2, .... п.

Матрица Т называется информационной матриц ей Фишера.

Матрица Т-, обратная ииформациоиной матрице, называется дисперсионной, или ковариационной, матрицей D(V*) оценок V (иногда ее называют матрицей погрешностей). Диагональные элементы этой матрицы определяют дисперсии оценок, а иедиагональные элементы - ковариации соответствующих им оценок (коэффициентов регрессии).

Определение оценок в соответствии с приведенной теоремой при сделанных предположениях означает фактически определение оценок по методу наимень-

ших квадратов. Поэтому оценки V*, полученные по последней формуле, обладают тем свойством, что минимизируют диагональные элементы матрицы D(V*).

Доказано также (см., например, [23.8]), что наилучшие линейные оценки V* обладают наименьшей дисперсионной матрицей D(V*) среди всех линейных несмещенных оценок и определитель [D(V*)] также наименьший, т. е.

D(V*XD(Vh*)

и

[D(V*)]<[D(Vb*)],

где Vh - вектор любых несмещенных линейных оценок.

Так как целью регрессионных экспериментов является получение оценок коэффициентов регрессии, то качество (или оптимальность) таких экспериментов и соответствующих им планов естественно оценивать в зависимости от точности получаемых в результате эксперимента оценок. Точность оценок V* характеризуется их дисперсионной матрицей D[V*], поэтому критерии оптимальности планов регрессионных экспериментов обычно формулируются в виде некоторых требований, предъявляемых к дисперсионной (а следовательно, и к информационной) матрице.

Прежде чем формулировать критерии оптимальности планов, уточним понятие плана регрессионного эксперимента. Учитывая, что в общем случае в каждой точке факторного пространства Yi может производиться несколько независимых измерений, планом регрессионного эксперимента e(N) называется сово-

п

купиость величии (Yi, п), (У^, Гя),2 i=N, где N - общее количество

измерений.

План называется £ -оптимальным, если он минимизирует определитель дисперсионной матрицы (соответственно максимизирует определитель информационной матрицы), т. е. -оптимальное планирование заключается в отыскании

min 1 D I

или

max I Т I .

е (n)

Определитель дисперсионной матрицы D (его называют также обобщенной дисперсией) характеризует объем эллипсоида рассеяния оценок V*, поэтому £ -оптимальный план минимизирует объем этого эллипсоида.

План называется Л-оптимальным, если он минимизирует след Sp (сумму диагональных элементов) дисперсионной матрицы

т

min S D = min У Dno-

Л-оптимальный план минимизирует среднюю дисперсию наилучших линейных оценок.

Кроме перечисленных критериев оптимальности находят применение также минимаксные критерии (например, минимум максимальной дисперсии функции отклика), информационные и др. Оказывается, что в некоторых частных случаях

план, оптимальный в смысле одного критерия, одновременно оптимален и по другим критериям. Например, планы, оптимальные по миинмаксному критерию, являются также С-оптима-ьными; если дисперсионная матрица имеет вид D= = С1, где С - константа, а единичная матрица, то план, которому соответствует такая матрица и который Л-оптимален, будет также С-оптимальным.

Задача построения оптимальных планов регрессионных экспериментов в общем случае является весьма сложной, поэтому ее решают обычно с использованием ряда ограничений (например, поверхность отклика является линейной ити квадратичной функцией независимых переменных и т. д.). В настоящее время наиболее разработана теория £>-оптимальных планов для линейной регрессии.

Планирование экспериментов по выяснению механизма явления

Эксперименты по выяснению механизма явления имеют своей целью определение математической модели, описывающей исследуемое явление (объект). При планировании таких экспериментов исследователь обычно располагает некоторой информацией об исследуемом объекте, и в зависимости от этой априорной информации возникают три различные постановки задач.

1. Математическая модель объекта априори известна, т. е. известен аналитический вид функции отклика (У, V) и требуется определить вектор параметров

или же известны не только вид функции б(У, V), но и предварительные оценки бо*, которые необходимо учитывать.

2. Известно, что функция отклика совпадает с одной из функций i (У, V), h(y, V), 1в(У, V), и требуется определить, какая из этих функций является истинной, и оценить ее параметры. При этом предполагается, что в различных моделях вектор параметров Vi (i=l, . , <?) может иметь различную размерность. Другими словами, перед экспериментом исследователь располагает несколькими возможными моделями (гипотезами) исследуемого явления, и задача состоит в том, чтобы поставить эксперимент, позволяющий выбрать такую модель, которая лучше всего соответствует исследуемому явлению.

3. Аналитический вид функции отклика (У, V) неизвестен, но известно (по крайней мере, предполагается), что функция отклика в интересующей исследователя области может быть с достаточной точностью аппроксимирована конечным рядом по некоторой системе наперед заданных функций (например, полиномом). Требуется поставить такой эксперимент, который позволил бы найти наилучшее описание функции (У, V).

Математический аппарат планирования экспериментов наиболее полно развит для решения первой из перечисленных задач. Применительно к этой задаче разработаны эффективные методы планирования как статических (планируется весь эксперимент в целом), так и последовательных (поэтапных) экспериментов. Методы статического планирования для широкого класса функций (У, V) разработаны настолько, что подобное планирование сводится, по существу, к выбо-

РУ готовых таблиц, описывающих оптимальные планы экспериментов. Некоторые трудности возникают в тех случаях, когда функция (У, V) нелинейна по оцениваемым параметрам V. Однако, используя линеаризацию функции - разложение ее в ряд Тэйлора в окрестности некоторой точки Vo* (точка предварительных оценок параметров), обычно удается и в этом случае решить задачу стандартными методами.

Достаточно полное описание методов решения первой задачи имеется-в [23.8], многие методы планирования и описания различных оптимальных планов можно найти в [23.7, 23.8].

Более сложной является вторая задача - планирование экспериментов по. выбору наилучшей модели из некоторой заданной совокупности; эта задача является, по существу, задачей дискриминации гипотез. Планирование дискриминирующих экспериментов заключается в поиске таких точек У, в которых конкурирующие гипотезы к У, Vi), .... lg{Y, Vg) давали бы разные результаты т. е. результаты измерений в этих точках не должны быть инвариантны к замене одной проверяемой модели другой. Здесь прежде всего возникают две основные задачи. Первая - это выбор совокупности конкурирующих моделей-гипотез. Естественно, что лучшие результаты могут быть получены тогда, когда число, конкурирующих моделей невелико, а их совокупность содерБ<ит истинную модель. Эту задачу должен решать специалист той облЗЪти науки, к которой относится планируемый эксперимент. Вторая задача - выбор некоторого оптимального решающего правила, позволяющего принимать илн отвергать конкретные гипотезы. В качестве таких правил можно использовать решающие правила, основанные на сравнении взвешенных сумм квадратов отклонений по критершо Х^, правила, основанные на критерии отношения максимального правдоподобия, на энтропийном критерии (мера Кульбака), и т. п.

Наибольшие трудности встречаются при планировании экспериментов в тех случаях, когда математическая модель исследуемого явления совершенно неизвестна. Оптимальные планы экспериментов при неизвестном виде функции. (У, V) в настоящее время еще не разработаны, н задача эта решается обычно, с помощью некоторой последовательной процедуры, предусматривающей чередование экспериментов по уточнению параметров и дискриминирующих экспериментов. Этот процесс поиска математической модели можно представить [23.8; в виде следующей схемы (рис. 23.2).

Блок 1 отображает экспериментальный этап работы, т. е. техническое осуществление ранее спланированных экспериментов (например, некоторых предварительных, затравочных экспериментов). Следующий этап (блок 2)-оценка) параметров V некоторой предварительной (может быть, грубой), но известной' модели (У, V). После этого (блок 5) проверяется, согласуется ли описание-функции к У, V*), где V* - вектор полученных оценок, с экспериментальными данными. Если согласуется, то эксперимент можно прекратить либо спланировать, его по дополнительному уточнению оценок (или некоторой наиболее интересной части этих оценок). На схеме, нзобраБ<енной на рис. 23.2, этому этапу соответствует блок 4. Если же модель (У, V) плохо согласуется с экспериментальным данными, то требуется пересмотр принятой модели путем более тщательного, анализа исследуемого явления и возможно построение новой модели (блок 5). Наконец, последний этап - планирование дискриминирующего эксперимента (блок 6), который позволил бы выяснить, какая из имеющихся моделей лучше описывает исследуемый объект.

При реализации такой последовательной процедуры поиска моделей используются, естественно, методы и критерии, применяемые при решении задач по уточнению или определению оценок параметров и по дискриминации моделей. Однако такое поочередное решение этих задач может привести к плохим результатам (будет выбрана модель, плохо описывающая исследуемое явление). Это связано с тем, что если выбрана неадекватная предварительная модель, то теряет смысл задача уточнения оценок ее параметров, а если параметры модели оценены грубо, то трудно осуществить правильно дискриминацию моделей.

Рис. 23.2. Схема процесса поиска математической модели:

1 - эксперимент; 2 - обработка экспериментальных данных и поиск оценок искомых параметров; 3 - проверка согласия между моделью и данными; 4 - планирование эксперимента по уточнению параметров; 5 - пересмотр модели и выдвижение конкурирующей модели; 6 - планирование дискриминирующего эксперимента

В связи с этим возникает весьма актуальная и вместе с тем сложная задача построения таких планов, которые были бы оптимальными и в смысле уточнения параметров, и в смысле дискриминации моделей. Здесь необходимо решить задачу выбора некоторых обобщенных критериев оптимальности. При разработке таких критериев обычно используют некоторые функции от известных частных критериев либо вводят новые критерии точности результатов эксперимента, учитывающие одновременно информацию и по определению оценок параметров, и по дискриминации моделей.

Обобщенным критерием первого типа может быть, например,

где М - мера, зависящая от качества дискриминации; Л - мера точности оценкч параметров; Hi, - весовые множители, которые должен выбирать исследователь.

Критерий К может означать конкретно потери при неправильном решении задачи. Тогда М будет характеризовать потери, вызванные неправильной дискриминацией модели, а Л - потери из-за неточного определения оценок неизвестных параметров. При использовании таких обобщенных критериев возникает трудность, связанная с выбором весовых множителей Ну и Н^.

Обобщенным критерием второго типа моБ<ет быть информационный критерий (например, среднее количество информации, приобретенной в эксперименте).

Краткое изложение методов планирования экспериментов при неизвестной функции К У, V) имеется в [23.7, 23.8].

Планирование экстремальных экспериментов

Необходимость в планировании экстремальных экспериментов возникает при решении различных экстремальных задач (задач оптимизации) в условиях, когда исследуемые объекты (процессы) представляют собой диффузные системы с неизвестными механизмами (математическими моделями) явлений. Типичными примерами таких задач являются задачи оптимизации различных химических, ме-

таллургических и биологических процессов, причем протекание каждого из них зависит от многочисленных факторов, влияние которых на процесс трудно поддается функциональному описанию. Поэтому и возникает задача экспериментального поиска оптимальных условий протекания диффузионных процессов, а следовательно, и задачи планирования таких экспериментов. Таким образом, планирование экстремальных экспериментов заключается в поиске таких значений факторов (контролируемых переменных), которые обеспечивают оптимальное в смысле некоторого критерия протекание процесса. Например, для определенного химико-технологического процесса критерием оптимальности может быть требование максимального выхода продукта реакции, а планирование эксперимента будет заключаться в поиске таких значений факторов (температуры, давления, концентраций реагентов и т. п.), которые обеспечивают это требование. Так как зависимость выходного продукта от факторов (поверхность отклика) априори неизвестна, то в этом случае используют полиномиальную модель, а для нахождения оптимальных значений факторов предусматривают при планировании изменення факторов в широких пределах. Однако проведение такого многофакторного эксперимента потребует, очевидно, очень большого числа опытов, времени и затрат. Чтобы избен^ать этого, планирование экстремальных экспериментов основывается обычно на шаговом методе изучения поверхности отклика [23.7], суть которого состоит в том, что вначале ставится небольшая серия опытов для локального описания небольшого участка поверхности отклика полиномом первой степени, далее осуществляется движение по поверхности отклика в направлении градиента линейного приближения, ставится новая серия опытов и т. д. Этот шаговый процесс продолжается до тех пор, пока не будет обнаружена некоторая почти стационарная область, где линейная модель уже непригодна. В этой области используются полиномы второй степени и планируется большая серия опытов.

Таким образом, планирование экстремальных экспериментов сочетает в себе идею движения по градиенту (крутого восхождения по поверхности отклика) с планированием многофакторных регрессионных экспериментов для локального описания поверхности отклика.

Следует отметить, что вопросы планирования экстремальных экспериментов разработаны в настоящее время достаточно полно, изложению соответствующих методов планирования и их практическому использованию посвящено значительное число работ.

ЗАКЛЮЧЕНИЕ

В данной книге систематизированы стрлктуры, алгоритмы функционирования и даны начала системотехнического проектирования ИИС и входящих в них системных устройств. Остановимся на перспективах их развития и попытаемся наметить задачи, подлежащие рещению в будущем.

В первую очередь можно выделить круг задач, связанных с соверщенствованием основных метрологических, эксплуатационных, экономических характеристик ИИС в рамках функций, выполняемых существующими в настоящее время системами. Даль-нейщее повыщение точности, быстродействия, чувствительности,