Таблица 21.1, Характеристики некоторых ортогональных базисных функций

Вид аппроксимирующей функции

Составляющие базисных функций

Интерполяционный многочлен Лагран-жа

Ряд Котельникова

sin Юс (t - jM)

Прибл.чжение многоч.тенами Чебышева первого рода

К

п

k (О = 1/К 1 - А; I - М/2, М/2]

Приближение многочленами Лежандра К

fe=C

Приближение многочленами Лагерра п

См. рис. 21. 1, 21.2

См. рис. 21.4

/ (<) = cos (я arc cos О .

Т, (О = 4/3 3/; = 8<* -8/2+1

(См. рис. 21.5, 21.6)

(t) = - (35/4 30/2 + 3) 8

L (/)=l; q(t)=-t + U

L5(0 = -4t+2:

Вид аппроКсими.зующеа функции

Составляощие базисных функций

Разложение Фурье - Уолша

п

См. ркс. 21.7

функции С экстраполяцией по предыдущему значению. Восстанавливающее устройство при этом имеет наиболее простой вид и не вносит запаздывания в процесс восстановления.

При равномерном приближении (штрихпунктирная линия на рис. 21.1) интервал дискретизации может быть увеличен вдвое, но при восстановлении исследуемой функции вводится запаздывание на интервал дискретизации и несколько усложняется реализация восстанавливающего устройства.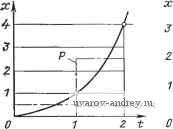

Рис. 21.1. Приближение Рис. 21.2. Приближение Рис. 21.3. Линейная ап-функции x{t)=P много- функции x(t}=fi много- проксимация членом нулевой степени членом первой степени

Если аппроксимация функции x{t) производится многочленом первой степени (линейная аппроксимация), то i<181 s, /M2, а восстановленная функция имеет вид х* {t)=x{ti)-\-[x{ti+i) - -x{ii)] {t-tj)/tj+i-ti. В нашем примере М2=2, а если €таж| = =0,25, то Д^1:1, т. е. достаточно иметь два интервала дискретизации (рис. 21.2).

При относительно больших значениях допустимой погрешности (етал:0,02) разница между интервалами при линейной аппрок-

Продолжение табл. 21 1

Погрешность

Информация о .vr(/)

Определение интервала дискретизации

симации и аппроксимации миогочлеиами более высокого порядка иезиачительиа. Поэтому лишь при малых погрешностях приближения целесообразно рассматривать возможность применения многочленов со степенью п>2.

Положим, что известна корреляционная функция /?*х(т) исследуемой функции x(t) и задана среднеквадратическая погрешность о приближения (Напомним, что использование среднеквадратиче-ского критерия погрешности аппроксимации возможно, если ис-

следуемая функция интегрируема в квадрате, т. е. x(t)dt<i оо.)

а

Тогда, если для аппроксимации реализации случайной стационарной функции x{t) используется степенной многочлен нулевой степени, интервал дискретизации может быть определен из выражения М* [x{t) -x{tj) Y=2R*x (0) -2R*x (Ato).

Когда корреляционная функция Rx*{t:) неизвестна, то значение Ato может быть определено путем последовательного приближения к допустимому значению среднего квадратического отклонения.

Для линейной аппроксимации (при максимальной погрешности на середине интервала дискретизации) в соответствии с рис. 21.3

= М* {х it) ~ к (t,.) + [X (/+.) - X {t)] } = = 1 М\ (0) - 2R {MJ2) + 0Ж\ (А..).

Нахождение значения Ati при известной функции /?х*(т) особых затруднений не вызывает.

По В. А. Котельникову непрерывная функция x{t), удовлетворяющая условиям Дирихле, с ограниченной верхней частотой fc

может быть представлена своими дискретами, следующими через интервалы Atl/2fc:

00 go

X(t)- 2j x(]M) (, .д;) - 2j -[-2]

/=-00 /=-00

Этот ряд носит название ряда Котельникова, а функция sinj[(2fc-j)/n(2fct-j) - функции отсчетов. На рис. 21.4 показаны произведения

X ( 2fс) [sin п {2Ut-j) /я (2fс/-У) ]

для моментов времени /-1, /, /+1.

Восстановление исходной непрерывной функции по дискретным отсчетам x{j/2fc) в виде б-импульсов через интервалы времени At=l/2fc может быть выполнено путем использования идеального фильтра нижних частот на бесконечно большом (от -оо .до оо) интервале времени. На практике исследуемые процессы длятся в течение конечного времени. Следовательно, математическая модель, отображаемая теорией отсчетов, лишь приближенно описывает реальные физические процессы. Нужно заметить, что отклонение характеристик фильтра от идеальных также вносит погрешности.

Ввиду сказанного при использовании теоремы Котельникова на практике несколько увеличивают значение расчетной верхней граничной частоты fc-

Известна математическая модель, в которой принимается, что спектр сигнала отличен от нуля в пределах от -оо до оо, сигнал имеет конечную длительность и известна его корреляционная функция. Для этого случая доказывается, что интервал дискретизации должен быть равен интервалу корреляции:

т. е. отсчеты функции по теореме Котельникова представляют со- бой не что иное, как ближайшие некоррелированные значения функции.

Для аппроксимации непрерывных ф^нкций широко используются ортогональные функции и многочлены. Основные их достоинства связаны с тем, что коэффициенты базисных функций могут получаться независимо друг от друга и во многих случаях они обеспечивают хорошую сходимость.

Напомним, что система функций фь ..., фк называется ортогональной на отрезке [О, Г], если

Здесь л является нормой ф^; если л=1, то функция называется иормированиой, а система ортогональных функций называется ортонормированной. Если (p{t) определена в точках ti, .... tn, та ее можно рассматривать как вектор п-мерного пространства с компонентами (pkitj). Тогда функцию x{tj) можно представить в виде

где

C,-\k{t)Xit) <f, (/)di jjk (t) f, it)dt

0 / 0

- коэффициенты Фурье, a kit) -весовые коэффициенты.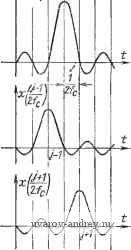

Рис. 21.5 Размещение узлов аппроксимации при использованиЕ многочленов Чебышева

To(t)

г

Рис. 21.4. Произведени.ч дискретных значений и функции отсчета

Рис. 21.6. Многочлены Чебышева

В табл. 21.1 приведены в сжатом виде данные некоторых ортогональных базисных функций.

Узлы аппроксимации многочленов Чебышева (рис. 21.5) определяются путем решения уравнения ? (/) =0. Они имеют гармоническое расположение (рис. 21.6), при котором узлы распределены гуще к концам отрезка наблюдения. Использование узлов Чебышева приводит к уменьшению погрешности аппроксимации по сравнению с равномерной дискретизацией.

ОстатОчный член многочлена Чебышева равен

[(М„+.Кя+ 1)/2 (/г + 1)П(А№

W3=R,Rz

Многочлены Чебышева во многих случаях дают лучшее и более экономное приближение, чем другие базисные функции.

Весьма удобно для практического использования при аппроксимации непрерывных функций и в ряде других приложений разложение функций в ряд Фурье с коэффициентами Фурье - Уолша [11.8]. В рассмотренных ранее ортогональных многочленах определенную трудность представляет формирование функций фк(0 ( В виде синусов, косинусов, степенных выражений и т. п.).

Разложение интегрируемой в квадрате на отрезке' [О, Г] функции x{t) в ряд Фурье с использованием функций Уолша Wy,{t) выполняется по формуле

>c4ti)=c,{ww,{t,).

Коэффициенты Фурье - Уолша

Рис. 21.7. Функции R и Уолша W

Радемахера

(при ции).

единичной весовой функ-

Система функций Уолша образуется из функций Радемахера (рис. 21.7). Функция Радемахера т-го порядка определяется при целых положительных т следующим образом:

Р^(/) = sign sin (2 +ii/),

или

+ 1, если ~<t<

. 2гЧ- 1

2п

(нечетные интервапы, начиная с 0); - 1, если -<<--

(четные интервалы i);

oW-1.

Здесь j=0, 1, ..., 2 --1 - порядковый номер интервала задания функции Rm{t).

Чтобы из функций Радемахера, являющихся нечетными, получить полную ортогональную систему, нужно образовать произведения вида (рис. 21.7).

.....mAi)=Kni)X...XR At).

Для построения функций Уолша может быть использовано следующее соображение. Функции Радемахера соответствуют делению отрезка [О, Т] на 2 . Следовательно, W2, W4, Ws . .. равны соответственно Ri{t), Rzit), Rsit), Rit) ... Формирование промежуточных (между двоичными) значений Wk осуществляется в соответствии с формированием чисел в двоичном коде. Например, Ws{f)=RAt)R2{t); W{t)=R.ii)R,(t)R,{t).

В некоторых случаях удобно использовать обозначения Wgi и Wei, введенные по аналогии с тригонометрическими функциями.

Процесс получения коэффициентов Фурье - Уолша соответствует умножению матрицы Уолша W [строки этой матрицы равны значениям функций Уолша в двоично-рациональных точках отрезка (О, Г)] на вектор-столбец исходных данных:

Для определения коэффициентов выполняются операции сложения и вычитания; умножения при этом отсутствуют.

Имеется возможность использовать так называемый алгоритм быстрого преобразования Фурье - Уо.пша, применив преобразование Адамара для каждой пары последовательных дискрет x{tj):

где

1 - матрица Адамара.

Для вычисления 2 коэффициентов Фурье - Уолша необходимо п раз последовательно применить это преобразование, и, следовательно, общее количество операций сложения и вычитания будет равно п2 .

Ряд Фурье с функциями Уолша для всякой функции x{t), интегрируемой на отрезке [-А 2/А 2], сходится к ней в среднем.

Остаточный член для ряда равен

2 (п + \)\ \ 2 )

Отсюда может быть определен интервал квантования по времени, необходимый для восстановления исходной функции с заданной погрешностью.

Имеется обобщение теоремы отсчетов (теоремы Котельникова) !на ряд Фурье -Уолша, согласно которому каждая временная функция x{t) полностью характеризуется дискретной последова-тельностью значений отсчетов x{mAt), взятых через At=l[2fc= = Г/2 +. При этом действительно соотношение

x(t)=. f x{mM)r,(t~mAt).

Гп it)

1-для 0<f< {-2)Т;

i О - для остальных значений t.

Между наивысшей частотой процесса и п имеется очевидная чгвязь:

fc=2-/T,

!где Т - продолжительность выборки непрерывной величины.

В заключение следует подчеркнуть, что выбор системы базис-сных функций для аппроксимации должен производиться с учетом Сведений, которые имеются об исследуемой функции перед выпол- нением измерения.

21.2. ОБ АДАПТИВНОЙ ДИСКРЕТИЗАЦИИ

В промышленном производстве и при проведении эксперимен-тальных исследований увеличиваются потоки измерительной информации, требующие документирования, срочной обработки и визуального вывода. В то же время в подавляющем большинстве случаев информационная избыточность этих потоков велика, поэтому имеется возможность уменьшить их интенсивность, а значит, уменьшить емкость устройств памяти, загрузку устройств обработки и передачи данных, обеспечить более легкое восприятие оператором необходимой для его работы информации.

Уменьшение потоков (сжатие) измерительной информации мо-.жет быть произведено так, что либо по сжатым данным может быть восстанов,яена исходная информация, либо такое восстановление становится невозможным, т. е. в последнем случае в про-щессе сжатия могут быть необратимо потеряны необходимые для этого информационные составляющие. Типичными примерами не- обратимого сжатия являются процессы контроля, получения статистических закономерностей случайных процессов и т. п.

Операциями сжатия измерительной информации с сохранени- ем возможности восстановления исходных данных являются операции адаптивной дискретизации непрерывных измеряемых вели-Чин и их аппроксимации с помошью приближающих функций минимальной сложности. В дальнейшем изложении остановимся главным образом на адаптивной дискретизации непрерывных величин, связанной с минимизацией числа дискрет.

в общем виде задача квазиобратимого сжатия измерительной информации может быть сформулирована следующим образом. Исходная функция x{t) или х{1) на отрезке [О, Т] или [О, L] представлена с заданной погрешностью функцией яз[/,(/), Gi ... .... aiv]. Величины {аг},-=1.....jv могут быть, например, равноотстоящими дискретами исходной функции. Предположим, что восстановление исходной функции с заданной погрешностью выполняется с помощью другого набора величин {bj}j=i.....м- Если M<iN,

то можно говорить о сжатии ивмерительной информации.

Основными характеристиками устройств, выполняющих операции сжатия измерительной информации, могут быть коэффициенты сжатия, погрешности восстановления и время, необходимое для определения {bj}. В качестве при вычислении коэффициента сжатия может быть принято количество равноотстоящих дискрет, обусловленное, например, теоремой Котельникова. Тогда коэффициент сжатия может быть определен как

Ki=N/M, или /C,( = 1-M/.V.

В случае адаптивной дискретизации для восстановления исходной функции необходимо измерять также координаты реализованных дискрет во времени или в пространстве. Эта операция иногда носит название датирования отсчетов. Тогда коэффициент сжатия уменьшится и будет равен:

K2=Nl{M+Mo), или /С2(>=1-(Л1+Мв)/ЛГ.

Естественно, что характеристики сжатия существенно зависят от принятого метода (алгоритма) обработки информации.

Можно различать однопараметрическую, двухпараметрическую и многопараметрическую адаптацию [21.3]. При однопараметриче-скои адаптации (при заданной длительности реализации исходной величины) в соответствии с ее видом может изменяться число дискрет (узлов аппроксимации) либо при фиксированном числе узлов может изменяться длительность реализации исходной величины.

В случае двухпараметрической адаптации изменяется как число дискрет, так и длительность реализации. Многопараметрическая адаптация связана не только с адаптивным квантованием по времени, но и с оптимальным квантованием по уровню дискрет.

Остановимся на случае однопараметрическои адаптации исходной непрерывной величины конечной и заданной длительности. В этом случае вид приближающей функции и оценки погрешностей выбираются заранее, а интервалы квантования по времени определяются в зависимости от текущего поведения непрерывной величины.

Частным, промежуточным между равномерным и адаптивным квантованиями, является кусочно-равномерное программное квантование (рис. 21.8). Такую разновидность дискретизации можно реализовать, если известен характер изменения x{t) и можно выделить отдельные участки, на каждом из которых устанавливаются