г л а в а 20

ТОЧНОСТНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ СИСТЕМ

20.1. КРИТЕРИИ ОЦЕНКИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ ВХОДНОЙ ВЕЛИЧИНЫ

В результате измерения неизвестной входной величины х получается ее приближенное значение х* (с погрешностью е). Под погрешностью понимается степень близости результата измерения к истинному значению измеряемой величины.

Погрешность измерения е вызывается, во-первых, неточностью изготовления аппаратуры, изменением ее характеристик во времени, чувствительностью к неконтролируемым внешним мешающим воздействиям у, а во-вторых, неточностью самого метода измерения. В соответствии со сказанным можно различать аппаратурную и методическую составляющие общей погрешности. Так как факторы, вызывающие появление погрешности измерения, вообще говоря, имеют случайный характер, то и погрешность измерения следует рассматривать как случайную величину [20.1, 20.2]

Наиболее полной характеристикой погрешности е вследствие возможности ее статистической связи с измеряемой величиной х является условная плотность распределения вероятностей f(sx), которая теряет условный характер и имеет вид f(e) при отсутствии такой связи. Плотность распределения вероятностей содержит всю необходимую информацию для оценки погрешности, однако она не всегда известна. Поэтому на практике используется некоторое количество параметров (показателей) этого распределения так, чтобы эти параметры в достаточной мере характеризовали погрешность исследуемой системы. В качестве оценок погрешности отдельных устройств и измерительных систем наиболее широко применяются экстремальные, интегральные оценки и оценки, основанные на применении доверительных интервалов и вероятностей.

К экстремальным оценкам погрешности относятся:

модуль максимального отклонения

S.max= IX-Х' max,

модуль максимальной относительной погрешности

модуль максимальной приведенной погрешности

8 =

пр у

К интегральным оценкам погрешности (если х и х* - случайные величины) относятся:

средний модуль отклонения

оо со

f(K, к*} IX - х*\ йхйк ;

-go -00

средний модуль относительной и приведенной погрешности

00 оо

00-оо 00 оо

-00-00

среднее квадратическое отклонение

з, = / J J/(3C, x)(x-Kydxdx*

-00 -со

или дисперсия

00 00

Dz= j (л;, K){x-xydxdx.

-00-00

Под знаком интеграла в качестве сомножителя стоит выражение совместной плотности распределения вероятностей измеряемой величины л: и ее приближенного значения х .

Оценки погрешности, основанные на применении доверительных интервалов и вероятностей, позволяют определить, с какой вероятностью (Зд погрешность системы ед не выходит за заданные пределы ±ео:

Р{ед<ео} = Рд.

Для определения доверительной вероятности по заданному доверительному интервалу в общем случае необходимо знание плотности распределения погрешности f(e):

В частности, для нормального закона распределения р{8д|<о}=0,68; р{8д|<2о}=0,95;

р{едКЗа} =0,997.

Если кривая плотности распределения погрешности неизвестна, но известна ее дисперсия De, то при Л1£=0 можно найти верхнюю оценку доверительной вероятности, воспользовавшись неравенством Чебышева:

Р*д^1-Де/ед2.

Оценка неравенством Чебышева дает завышенные значения до-шерительных вероятностей, особенно для малых отношений

При выборе допустимых погрешностей отдельных устройств или систем, а также для их сравнения в ряде случаев широко используются так называемые функции штрафа (потерь). Функция штрафа определяет размер штрафа, налагаемый в случае наличия разницы между истинным значением измеряемой величины и ре зультатом измерения. Разумными требованиями к функции штрафа могут быть:

а) любая погрешность облагается штрафом

б) при отсутствии погрешности штраф равен нулю

к(х, х)=0;

в) большие отклонения х* от х облагаются большим штрафом, т. е. для л:л:1*л:2*

%{Х, Xi*)k{x, Х2*).

в качестве функции штрафа наиболее часто используются различные оценки погрешности, взвешенные соответствующими коэффициентами.

Так как в общем случае х п х* - случайные величины, то и функция штрафа является случайной величиной. Можно произвести усреднение выбранной функции штрафа щ при фиксированном значении Xi (так называемый условный риск):

g{xi, х')= iiiXi, x)fixfXi)dx,

и для всех возможных значений х п х* (так называемый средний риск):

00 00

G{k, х^)= j %j{x. Kjfix, xf)dxdx.

-00-00

Для характеристики средства измерения нужно знать условную плотность вероятностей f{x*/x) результатов измерения х* при фиксированном значении измеряемой величины х. Считается, что при измерении величины х, имеющей плотность распределения вероятностей f{x), измерительная система 1 не хуже измерительной системы 2 по критерию О, основанному па функции штрафа v.j{x, л-*), если

j %,{х, x)f,{x, x)dxdK< J Kjix, x)h{x, x)dxdx.

При оптимизации измерительных систем в качестве критерия оптимальности используют средний риск, добиваясь min min Gx Х(л:, X*) (минимальный критерий) или minmaxG(A, х*) (минимаксный критерий). Последний критерий применяется тогда, когда должна быть гарантирована минимальная погрешность при любых законах распределения вероятностей f{x).

Универсальных оценок, пригодных для сопоставления между собой различных ИС, не существует. Можно показать, что, пользуясь даже одной оценкой, одно и то же средство измерения можно, признать лучшим или худшим чем другое, в зависимости от вида закона распределения вероятностей измеряемой величины.

Уместно назвать некоторые разумные области использованиж тех или иных оценок.

Так, экстремальные оценки целесообразно использовать в таких случаях, когда важно оценить, насколько результаты измерения могут отклониться от действительного значения. Такие оценки важны при исследовании, положим, процессов, проходящих вблизи аварийных ситуаций, при исследовании предельных значений прочности силовых конструкций и т. п.

Для оценки погрешностей измерения, предположим, количества выпускаемой продукции при непрерывном производстве или вообще для оценки ИС в среднем правомерно использовать интегральные оценки и оценки, основанные на применении доверительных интервалов и вероятностей.

Таким образом, соответствующие оценки погрешности должны выбираться в зависимости от характера измеряемой величины, от целей использования результатов измерения и свойств' измерительной системы.

20.2. ОЦЕНКА ПОЛНОЙ ПОГРЕШНОСТИ

Если составлена СЛСА системы, то в ней можно выделить преобразования измерительной информации, сопровождающиеся погрешностями.

Очень важной задачей является определение полной погрещности ИИС по характеристикам погрешности этих функциональных преобразований или выполняющих их блоков..

В этой задаче можно выделить два предельных случая:

определение полной погрешности одноканальнон (последовательной) многоблочной ИИС;

оценка погрешности ИИС многоканальной (параллельной)-структуры.

Вопросы определения полной погрешности ИИС смешанной параллельно-последовательной структуры решены пока с недостаточной для практики полнотой.

Наиболее разработанной является задача определения полной статической погрешности многозвенных последовательных измерительных систем. Методы, применяемые для ее решения., зависят от того, в какой форме заданы погрешности отдельных звеньев, за-

даны ли их законы распределения или заданы только некоторые числовые характеристики частных погрешностей.

Рассмотрим применяемые в названных случаях методы.

Если известны аналитические выражения для законов распределения погрешностей отдельных звеньев и система линейна, то задача может быть решена с помощью методов свертки или с ис-.пользованием характеристических функций.

Пусть, например, ei и ег - случайные функции погрешности двух соседних звеньев, а f(ei) и ({г^) -их плотности распределения. Тогда, если эти погрешности независимы, закон распределе ния суммарной погрешности ei,2 этих двух звеньев находится с помощью свертки исходных плотностей:

Применяя последовательно операцию свертки п-1 раз, где п- количество звеньев, получаем закон распределения полной погрешности системы.

Использование метода характеристических функций заключается в следующем. По теореме умножения характеристическая функция суммы независимых случайных величин определяется как произведение их характеристических функций, т. е. в нашем случае

п

где

- характеристическая функция погрешности t-ro звена; g{Ks.) - характеристическая функция суммарной погрешности системы.

Выполнив затем обратное преобразование, можно найти закон распределения полной погрешности f{&s.) системы.

Следует отметить, что инженерное решение задачи определения полной погрешности данными методами в большинстве случаев может быть получено лишь после преодоления трудностей, связанных с вычислением многомерных интегралов.

В настоящее время все большее значение приобретает развитие методов решения задачи определения полной погрешности, основанных на математическом моделировании. К ним относятся метод статистических испытаний (СИ) и метод деревьев логических возможностей (ДЛВ). Оба метода позволяют определить закон рас пределения полной погрешности как в случае, когда законы распределения погрешностей отдельных звеньев заданы аналитически, так и в случае, когда эти законы заданы в виде гистограмм.

Метод СИ является более разработанным и известным методом, чем метод .ДЛВ. Сущность использования метода СИ для определения полной погрещности ИС заключается в следующем. Законы распределения случайных первичных погрешностей формируются с помощью специальных генераторов или программным путем. Осуществляя многократный перебор случайных сочетаний значений первичных погрешностей и определяя каждый раз полную погреншость, можно по результатам испытаний воспроизвести закон распределения полной погрешности ИС. Принципиально метод CPI не менее точен, чем аналитические методы расчета, но для получения высокой точности определения полной погрешности он требует перебора весьма большого количества случайных сочета НИИ первичных погрешностей.

Использование метода ДЛВ для определения полной погрешности многозвенных ИС менее известно, поэтому представляется целесообразным отстановиться на этом методе более подробно. Сущность метода ДЛВ заключается в следующем [20.3]. Пусть имеется некоторое пространство логических возможностей. В этом пространстве может быть построено так называемое дерево, представляющее собой связный граф, в котором нет ни одного контура. Каждой ветви дерева приписывается некоторая вероятностная мера, представляющая собой безусловную или условную вероятность получения отдельных первичных погрешностей или возможного сочетания различных первичных погрешностей. Законы распределения погрешностей при использовании метода ДЛВ представляются в виде дискретной последовательности возможных значений первичных ошибок е, каждому из которых приписывается определенная вероятность. Любое отдельное сочетание случайных значений различных первичных погрешностей представляет собой реализацию, вероятность которой определяется вероятностями выбранных значений первичных погрешностей. Каждая полученная описанным образом реализация образует вполне определенный путь в ДЛВ, и для нее сравнительно легко гшределить вероятность.

Разберем на примере, заимствованном из [20.3], графический способ построения ДЛВ. Предположим, что рассматривается система независимых случайных величин а, Ь, с, каждая из которых может принимать несколько дискретных случайных значений а bj, Ck (например, i=j=k=l, 2, 3) с заданными вероятностями р

Pb.Pch дальнейшем для простоты вместо а;, bj, Ch будем писать

i, /. k.

Для независимых случайных величин процесс построения ДЛВ можно начать с любой из них и в произвольной последовательности. Вероятность появления каждой из возможных реализаций может быть записана так:

P[i/\iAk]=p[i]pi[j]Pi =PiPHjPij,h. Последние два сомножителя в приведенном выражении последовательно указывают выбранный путь на ДЛВ. В более общем

Pzzz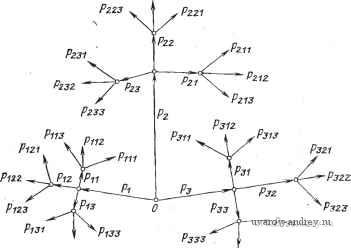

P13Z

P33Z

Рис. 20.1. Пример построения дерева логических возможностей

случае, когда случайные величины статистически зависимы, ве-ро.ятности р,-,з и pi,j,\i являются условными. ДЛВ, построенное для рассматриваемого случая, изображенно на рис. 20.1.

Точка О на рис. 20.1 называется корнем дерева. Отрезки прямых Pi называются ветвями первого ранга, отрезки прямых - ветвями второго ранга, отрезки прямых pt,j,h - ветвями третьего ранга. При построении ДЛВ ветви всех рангов откладываются в едином масштабе, поэтому схеме ДЛВ присуща определенная наглядность. По ветвям наивысшего ранга можно определить число логических возможностей. Для рассматриваемого примера их ко-количество vV=27.

Вместо изображенной на рис. 20.1 схемы ДЛВ можно составить эквивалентную таблицу, в которой отражены вероятности каждого из путей дерева (табл. 20.1).

В общем случае изложенным образом может быть построена схема ДЛВ с ветвями т-го ранга или составлена эквивалентная ей таблица. При этом если через щ обозначить число дискретных значений случайной величины с номером /, то число путей в ДЛВ окажется равным:

где L - число случайных величин.

Т аблнца 20.1. Вероятности логических путей

Логический путь

Вероятность

Логический путь

Вероятность

Логический путь

Вероятность

Ol33

Ли Pus

Pill

PlW Pl23 PlSl Pl32

Лзз

02,3

O222 О22З O2S1 O232 О23З

All P2I2 P213 P22I P222 Р22З / 231 P2S2

O3II C312 O313 O321 O322 O323 C33I O332 O333

Psu P312 A13 A21

PS22 PS23

Pssi

PSS2

Сами пути будут иметь вероятности, определяемые выражениями

... ХР

П1 2 ... п.

рЫКрШХ ... -ХрЫ

в зависимости от того, являются ли случайные величины связанными или независимыми в статистическом смысле.

При относительно большом количестве случайных величин или их дискретных значений можно ограничиться одной табличной формой записи ДЛВ, а расчеты вероятностей различных логических путей проводить с помощью ЭВМ. По результатам этого расчета монсет быть построена гистограмма распределения результирующей суммарной величины.

Как показано в [20.3], метод ДЛВ может успешно использоваться для анализа по-решностей не только линейных, но и нелинейных систем, а также для случаев, когда случайные погрешности отдельных звеньев представляют собой не случайные величины, а случайные функции.

До сих пор речь шла о нахождении полной погрешности многозвенной измерительной системы по известным законам распределения. Как же следует поступать в тех случаях, когда частные погрешности заданы в виде некоторых числовых характеристик?

Если отдельные звенья ИС охарактеризованы экстремальными погрешностями, то полная погрешность системы определяется простым суммированием этих погрешностей. Естественно, такая оценка полной погрешности будет очень завышена.

Оценка полной погрешности может быть получена, если частные погрешности отдельных звеньев заданы интегральными оценками или доверительными интервалами и вероятностями. Методика определения полной погрешности для этого случая рассмотрена в [20.1, 20.2].

Несмотря на некоторое различие в подходе к решению этой задачи, по результатам проведенного анализа можно сформулировать некоторые выводы. Полная систематическая погрешность многозвенной линейной ИС находится суммированием систематических погрешностей отдельных узлов (если, конечно, известны действительные систематические погрешности узлов, а не их доверительные интервалы, в последнем случае можно получить грубую верхнюю оценку), а дисперсия случайной погрешности при условии некоррелированности погрешностей отдельных звеньев - как сумма дисперсий погрешностей звеньев (в случае, если погрешности некоторых звеньев коррелированы между собой, к сумме дисперсий добавляются удвоенные корреляционные моменты соответствующих погрешностей). При суммировании вводятся весовые коэффициенты, зависящие от схемы включения звеньев и определяемые как частные производные от выходной величины системы по величине на входе данного звена. В том случае, если заданы не дисперсии случайных погрешностей отдельных звеньев, а их доверительные интервалы, для определения полной погрешности необходимо знание законов распределения частных погрешностей.

По известным законам распределения частных погрешностей, доверительным интервалам и вероятностям можно найти дисперсии, а затем полученные дисперсии суммировать.

Если же законы распределения частных погрешностей неизвестны и заданы только их доверительные интервалы, то расчет полной погрешности становится крайне затруднительным. Из-за этого в качестве критерия погрешности отдельных звеньев предпочтительнее использовать среднее квадратическое отклонение или дисперсию.

В заключение следует сказать несколько слов о погрешности, с которой может определяться полная погрешность системы. В зависимости от решаемых задач эта погрешность должна выбираться разной. В обычных случаях эта погрешность может составлять примерно 30% максимального значения результирующей погрешности.

Оценка погрешности ИС многоканальной (параллельной) структуры молсет проводиться с учетом следующих соображений [13.5]. Систематическая погрешность такой системы находится как среднее арифметическое систематических погрешностей Ме каждого из N каналов. Среднее значение случайной погрешности в каждом из N одинаковых каналов должно быть равно нулю, поэтому равно нулю и среднее значение случайной погрешности системы в целом. Дисперсия случайной погрешности системы равняется среднему значению дисперсий случайной погрешности Dc в каждом канале.

Если в системе не все каналы однородны, а имеется несколько различающихся между собой групп однородных каналов, то такие средние показатели могут формироваться для каждой группы в отдельности.

20.3. О РАСПРЕДЕЛЕНИИ ПОГРЕШНОСТЕЙ МЕЖДУ ЗВЕНЬЯМИ СИСТЕМЫ

Значительный интерес при проектировании ИС представляет обратная задача оценки погрешности ИС, а именно задача распределения частных погрешностей по звеньям так, чтобы результирующая погрешность не превосходила определенного значения.

В общем случае решение такой задачи неоднозначно.

Остановимся несколько подробнее на результатах решения одной из модификаций обратной задачи, изложенных в [13.5]. Метод решения, предлагаемый в этой работе, основан на минимизации затрат:

где Сгъг - затраты на уменьшение погрешности t-ro узла; Cohi&i - потери при эксплуатации системы за счет наличия погрешности t-ro узла; е-г - некоторая оценка частной погрешности i-ro узла; Ci - удельные затраты на снижение погрешности i-ro узла; hi - коэффициент влияния частной погрешности i-ro узла на результирующую погрешность системы; Со - коэффициент, связывающий потери при эксплуатации системы с погрешностью i-ro узла; N-количество узлов в системе; q-некоторый эмпирический коэффициент: q>0.

Оптимальные значения погрешностей узлов Вг, минимизирующие 5, определяются как

Необходимо оговориться, что при проектировании, коэффициенты Со, Сг, hi зачастую неизвестны. Особенно трудно получить значение Cq. Не располагая знанием Со, задачу оптимального распределения частных погрешностей е, можно решать, если известно, каким значением ограничена сверху сумма допустимых затрат на уменьшение погрешности. Для этого случая и при q=l (т. е. затраты принимаются обратно пропорциональными погрешностям) получено выражение

где е^бщ = 2 ~ оценка полной погрешности системы.

Результат показывает целесообразность распределения частных погрешностей при ограниченных средствах на их снижение пропорционально весовым коэффициентам ]/с^ г^, характеризующим фактически эффективность вложений в целях снижения каждой ошибки.