о 0,005 0,01 0,015 0,0г 0,025 0,03 р^а/г

Рис. 13.5. Номограмма: заданы а, 1/аж\ находятся

36;.,%

0,005 0,01 0,015 0,0Z p-=J3/Z

Рис. 13.6, Номограмма: заданы Р, 1/ох; находятся 30 г Д, За у 1сx

По номограмме на рис. 13.7 при заданных (а+Р) и 1/ох можно определить допустимые погрешности контроля.

Следует отметить, что для определения ошибок контроля первого и второго рода могут быть использованы и иные методы. Например, если известны законы распределения годных f\{x) и негодных /о (л;) изделий по данной контролируемой величине и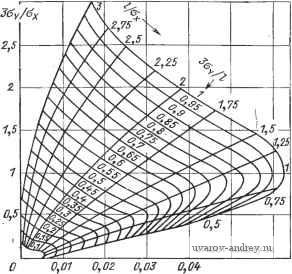

P=(oc+fi)/Z.

Рис. 13.7. Номограмма: заданы (a-J-p), l/Ox; находятся ЪотИ, Зот/Ох

если они частично перекрываются (рис. 13.8), то для данной нормы с можно определить вероятности отнесения годных изделий по данной контролируемой величине в негодные и наоборот.

В [13.7] рассматриваются асимптотические приближения оценки, также позволяющие существенно упростить вычисления Ws- 16- Остановимся кратко иа этих оценках.

fifjc)

Рис. 13.8. Плотности распределения вероятностей годных и негодных изделий

При принебрежении вероятностью реализации погрешностей, превышающих длину отрезка [Сн, Св], т. е. при р[у|>Св- -Сн] 0, и симметричной относительно нуля плотности вероятности величины у, т. е. при Ф( /) =ф(-г/),

1 Г(Сн)+Г(Св)

2 F(c)~F(c)

М[\у\\.

в этом выражении f -обозначение интегрального закона

распределения х, а М[\у\\= j /ф(у)ф -первый абсолютный

момент погрешности.

Для нормального распределения величин хну, имеющих характеристики Gx, Мх, Оу, My=Q, М[\у\]~2ау1У^\

оу ехр [ - (Св- А!)2/2оу + ехр [ - (Сн - М^)12<,\

Ф(Св--Ф(с^ - М^1=)

Ошибка первого рода (риск поставщика) может быть приближенно определена по формуле

W;.{F{c,)-F{c,)\Wl. Выражение для IFar-г существенно упрощается, если границы

интервала [Сн, Св] симметричны относительно Мх, т. е. Св-Мх= -Мх-Ск=кОх:

оу ехр [ - ft2/2]

Полученные выражения пригодны для решения обратной задачи, т. е. по заданному значению вероятности ошибки, например Wш-т, возможно определение ограничений на погрешность средств контроля:

exp[-ftV2]

Рассмотренный способ вычислений ошибок контроля пригоден для использования при инженерных расчетах с погрешностью

примерно 5-10%.

В ряде случаев удобно пользоваться понятиями, связанными с достоверностью контроля. Под достоверностью контроля понимается мера определенности решений, принимаемых при контроле.

Без выполнения контроля риск изготовителя а=0, а риск потребителя Рот может быть определен после оценки и (см. рис. 13.2), при этом абсолютная априорная достоверность

D=\-pom.

Рис. 13.9. Нормальное состояние гт г1в 4tB *г объекта контроля - площадь круга

Если контроль произведен с помощью технических средств с погрешностью, характеризующейся плотностью распределения в ероятностей f {у), то апостериорная абсолютная достоверность контроля D* = = I - = 1 ~ (** + Р*) Обычно < р^, и, следовательно, D*y-D. Относительная апостериорная достоверность контроля DoTB= 1 - (jCom/jCom)- До выполнения контроля Doth = 0, а после вы пол нения контроля Doth-1-

Следует упомянуть, что если состояние объекта характеризуется несколькими связанными друг с другом величинами, то при выполнении допускового контроля могут возникнуть дополнительные методические погрешности [13.2]. Так, если нормальное состояние объекта контроля определяется площадью круга, радиус которого R=Vk -\-к^ зависит от размера величин х\ и Х2, то в зависимости от того, каким образом выбираются уставки

СПн, Спв и Ci2H, С\2ъ ИЛИ С2\и, С^\ъ И оЗн, С22в , уВСЛИЧИВаЮТСЯ ОШИб-

ки второго ИЛИ первого рода из-за того, что уставками увеличивается или за счет негодных изделий число годных (заштрихованная площадь на рис. 13.9), или за счет годных число негодных (затушеванная площадь).

13.4. ОБЪЕМ ВЫБОРКИ ПРИ КОНТРОЛЕ

Выше рассматривался случай, когда не накладывались ограничения на количество объектов контроля. На практике для контроля из партии изделий выбирается некоторая часть. Последовательность реализованных значений хи--;Хп будет состоять из частных реализаций случайной величины X. Предположим, что закон распределения вероятностей этой величины нормален и имеет параметры Мх=а и Ох-

п

Оценки математического ожидания выборки М^х^ х;,-/ идис-

п

пенсии (а^хУ {Xi -М*хТIn сами являются случайными величи-

нами, изменяющимися от выборки к выборке.

Определим объем выборки, необходимый для нахождения Мх* с заданной абсолютной погрешностью ±А:

М[М'х] = а; Г! /

D[M*x]D

-1=1

При равенстве дисперсий математических ожиданий

D[Mx*]=Dx/n; °[M x]oxll1i.

Зададимся вероятностью Рдоп, с^ которой значения УИх -а должны лежать в пределах (-Д, Д):

р{-Д< (Мл-*-а) <Д}=рд

или после нормировки

д

По таблице функций Лапласа Найдем значение-Д/(с^/] г ) = /zon

[(например, при Рдог = 0,95; /1дог = 1,96). При допуске Д на значение \М*-а\ и известном Ох находим необходимый объем вы- борки:

/гдсша'/Д'.

Например, при рдоп = 0,997, а.х/Д=5 п~22Б.

Если совокупность контролируемых изделий ограничена, то следует для определения объема выборки пользоваться формулой

п С. Л [(Л' - 1) А^с^х Ч-Сп].

При N=500, рдоп=0,997 и ах/А=5 и=155.

Возможен несколько иной подход к определению необходимого объема Выборки. При последовательном анализе объем выборки заранее не определяется, а выполняется анализ поступающих нарастающим образом данных о значениях контролируемых величин (по сути дела производится измерение этих величин). После проверки принятой статистической гипотезы принимается решение о прекращении или продолжении контрольного эксперимента.

Положим, распределение вероятностей величины X нормально, известны Ох, значения уставок Сн и Св, а также ошибки первого и второго рода при контроле. Приемочные и браковочные числа при контроле среднего значения контролируемой величины могут быть подсчитаны по формулам

Здесь г-1, 2,..., N - количество последовательно контролируемых объектов.

На рис. 13.10 показаны зоны брака и годной продукции, а также зона неопределенности - продолжения эксперимента. После каждого измерения производится подсчет Xi к эта сумма

сравнивается с и щ. Если OjS Xtfi, то эксперимент продол-

жается. Если 2 х,С^)\, вся контролируемая партия изделий бра-

куется, а при 2 i<C4 принимается.

Последовательный анализ может быть использован также и при оценке среднего квадратического отклонения контролируемых величин.

На практике метод последовательного анализа дает относительно большую экономию в среднем числе испытываемых изделий по сравнению с фиксированным объемом выборки. Однако при его использовании заранее невозможно установить срок окончания контроля.

Имеется возможность использования смешанного метода контроля - заранее определяется необходимый объем выборки (п объектов контроля), затем контроль выполняется по методу по- , ,

х, г с , -Рис. 13.10. Использование последо-

следовательного анализа. Если звательного анализа при контроле для получения ответа о годности партии объектов контроля по методу последовательного анализа запланированный объем выборки недостаточен, то производится оценка результатов контроля по методу фиксированного объема выборки.

10 п

13.5. ОРГАНИЗАЦИЯ СТАТИСТИЧЕСКОГО КОНТРОЛЯ

Основная цель статистического контроля связана с получением статистических данных, необходимых для анализа хода технологического процесса или годности готовой продукции и для принятия соответствующих решений.

В случае, если заданы допуски годности продукции и доли годных и негодных изделий Wro, -во, Who, то текущий статистический контроль позволяет следить за ходом технологического процесса. При изменении положения центра настройки технологического процесса (рис. 13.И) происходит изменение вероятностей получения годных и негодных изделий. Для унимодальных и симметричных относительно начального центра настройки законов распределения f{x) в случае, показанном на рис. 13.11, справедливы следующие неравенства:

Увеличение рассеяния готовой продукции приводит к деформации распределения f(x) (рис. 13.12), и при ограничениях, отмеченных выше, соотношения между начальными и текущими зна

чениями вероятностей принимают вид

г1<1Гго; Wei>irEo; U7hi>U7 o.

Решения о перенастройке технологического процесса по данным статистического контроля принимаются на основании экономических соображений.

Статистический контроль можно организовать и в том случае, когда известен результат контроля в виде градации годен (Г) и брак (Б).

Рис. 13.11. Влияние изменения математического ожидания контролируемой величины на результат контроля

Рис. 13.12. Влияние изменения дисперсии контролируемой величины на результат контроля

Наиболее простым в этом случае является определение момента переналадки по предельному значению подряд встречающихся бракованных изделий в ряду ГБГГГББГГГГБББГ... [13.8].

Остановимся на основных методах уменьшения ошибок первого и второго рода.

Если продукция признается годной без допускового контроля или при зоне допуска [сн, Св]±3ал-, то ошибка первого рода отсутствует или пренебрежимо мала.

Уменьшения ошибок первого и второго рода можно добиться путем многократного повторения операций контроля. Однако эффективность многократного повторного контроля относительно невелика. Так, например, если объем действительного брака в партии изделий, контролируемый параметр которых распределен по нормальному закону, составляет 2%, то при нормальном распределении погрешности измерений и отношении предельно допустимой погрешности к ширине допуска, равном 0,2, ошибки первого рода будут достигать после первой операции контроля 17,5%, после второй операции контроля над отбракованными изделиями- 12%, после третьей -9,5% и после четвертой - 8%.

Значительно более эффективным оказывается двукратный контроль, при котором при первой операции используются менее точные, но более производительные средства, а при второй - более точные средства контроля. Если партия изделий содержит 3% действительного брака и проконтролирована с погрешностью

0,5 ширины допуска, то слиибка первого рода будет достигать 28%.. После второй операции контроля объем ложного брака составит 190/0. Если же вторая операция контроля будет проведена с ногрештостью 0,1 ширины допуска, то объем ложного брака составит 2%..

Для резкого уменьшения ошибок второго рода применяются-гарантированные допуски: это значит, что зона допуска Сн, Св сужается до размеров, при которых (3 становится пренебрежительно малой. Очевидно, что при этом должны увеличиться ошибки.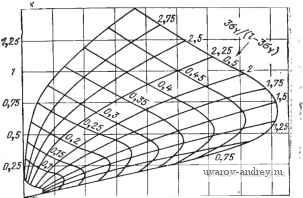

о о,ог 0,0 0,06 0,08 0,1 0,12 0,П р=а./2 Рис. 13.13. Номограмма: заданы а и (I-Зау)/о^с

первого рода. Для того чтобы ошибки не превышали заданного значения, необходимо обеспечить определенную точность устройства контроля.

На рис. 13.13 приведена номограмма, позволяющая оценить необходимую точность устройства контроля, если зона допуска уменьшена на Зоу, т. е. равна /-Зоу, заданы ошибки первого рода а и отношение зоны допуска к среднему квадратическому отклонению контролируемой величины.

Для принятого на номограмме диапазона изменения характеристики точности устройства контроля Зоу максимальное значение ошибки второго рода не первышает 10 ~*. Чтобы ошибка первого рода не была больше, чем при допуске негарантированном, необходимо существенно повысить точность устройства контроля. Так, например, для а+р-0,04, 1/ах=2,5 при негарантированной зоне допуска Зау = 0,87 (см. номограмму на рис. 13.7), а для гарантированной зоны допуска [1-3oy] при а==0,04, р=0,0001, 0=2,5 точность устройства может быть оценена выражением 3gy/10,3.

Типичными примерами специализированных устройств статистического контроля являются устройства для автоматического построения. гистограмм параметров радиодеталей, для получения

оценок математического ожидания и дисперсии размеров обрабатываемых деталей на станках и т. п.

Статистическая обработка экспериментальных данных выполняется с помощью выпускаемых промышленностью статистических анализаторов (см. гл. 15) и выполняется обязательно в САК, содержащих универсальные программируемые вычислительные устройства.

13.6. ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНОЙ КОНТРОЛИРУЕМОЙ ВЕЛИЧИНЫ

Необходимость дискретизации непрерывных контролируемых величин {x{t)} возникает при проведении операций контроля через некоторые интервалы времени, обусловленные, например, тем что устройство контроля в этих интервалах загружено определением состояния других величин.

Такой контроль называется далее дискретным в отличие от непрерывного контроля, при котором устройство контроля, не отрываясь, определяет состояние только данной контролируемой величины.

Положим, что известно поведение контролируемой величины во времени и оно описывается степенным многочленом x(t) - = Go+flJi+%+ +Gm - Тогда для ДОПУСТИМОГО изменения этой величины aon=ait+a2t+...-{-amt можно найти интервал времени At, через который необходимо провести операцию контроля состояния объекта.

Если заданы вероятность и интенсивность отказов и их связь со временем, например, выраженная в виде экспоненциальной функции р = е~*, то может быть определен интервал времени, через который следует произвести операции контроля объекта.

При дискретном контроле случайной величины x{t) для определения интервалов дискретизации не удается непосредственно использовать математический аппарат теории дискретизации, применяемый при измерении. Это объясняется в первую очередь спецификой контроля как процедуры сжатия информации.

Произведем сравнение среднего времени выхода контролируемой величины за зону допуска с интервалами дискретизации при равномерном и адаптивном допусковом контроле.

Рассмотрим в качестве предельного случай непрерывного контроля (рис. 13.14), характеризующийся тем, что устройство контроля фиксирует все выходы контролируемой величины x{t) за установленную зону нормального состояния [Сн, Св]. Примем следующие допущения: Рис. 13.14. Случай непрерыв- контролируемая величина являет-ного контроля ся стационарной случайной функцит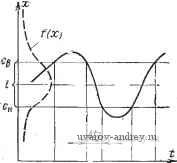

ей времени с нормальной плотностью распределения вероятностей

\время, затрачиваемое на контроль, пренебрежимо мало. Среднее число операций контроля, фиксирующих выход контролируемой величины за [Сн, Св], в течение времени Т равно:

где о^х - дисперсия контролируемой величины, а cv.- дисперсия

ее первой производной.

Суммарное время нахождения контролируемой величины в

пределах [Сн, Св] равно 2 Ш = рТ, где р - априорная вероят-

ность нахождения контролируемой величины в зоне [Сн, Св].

Среднее время между переходами контролируемой величиной уставок в этом случае составит:

Если учесть, что 1 I <

ехр

+ехр

И обозначить 2cj. /1/211 через , то А^ .ср = /К--

При контроле непрерывной величины через некоторые интервалы времени достоверность контроля по мере увеличения этих интервалов, естественно, снижается.

Допустим, что в момент tn выполнена операция контроля и установлено, что контролируемая величина находится в зоне [сн, Св]. В этом случае можно считать, что до следующей операции контроля с определенной вероятностью она останется там же. Тогда оценкой результатов контроля может служить вероятность р{Х^1) того, что при t>tn контролируемая величина не выйдет за [сн, Св].

На малом отрезке времени изменение контролируемой величины может быть представлено в виде

л:(г+АО .*;(7г)-ЬJt(< )A,

где x{tn-\-bX)\ x{trCi и x{tn) - соответственно размер контролируемой величины в моменты < -j-A и производной контролируемой величины в момент tn выполнения предыдущей операции. Чтобы контролируемая величина через время Д/ вышла за пределы [сн, Cj,] через границу Св, должно быть выполнено условие