коррелированной выборке определяется по формуле

при k=0, 1, , .., (m-1).

Здесь Мт - интервал сдвига, а тАх -интервал корреляции. При некоррелированной выборке и Д^Дт

(m-l)

(2m-1)

л;(Ш)(Ш + Мт)+ х(Ш)л(Ш +

+ Дх)+...+ (гДОл(Ш +Mt)

i=yv-m

В [12.7] подробно рассматриваются возможные режимы работы коррелометров параллельно-последовательного действия. Остановимся на одном из режимов работы такого коррелометра.

После аналого-цифрового преобразования (рис. 12.22) результаты измерений заносятся в регистры RGx и RGy. В запоминающем устройстве RAAlx хранятся результаты измерений мгновенных

о

значений x{iAt), взятых через интервал времени Д^-Дт. Количество в RAMx результатов измерения определяет количество измеряемых коэффициентов корреляции. В течение интервала At производится последовательное умножение всех запомненных значений

x{iAt) {i-0, 1, 2, ..., т) на реализовавшееся значение yijAt). По-

лученные произведения [x{iAt)y{jAt) при t=var и /=const] суммируются и хранятся в ЗУ. После выполнения этих операций, продолжающихся в течение Д^, производится измерение следующих

дискретных значений: х{т-г1, At) и у{т-\-1. At). В запоминающее

устройство RAMx заносится значение х{т-\-1. At) и убирается избыточное. В системе имеется возможность следить за текущими значениями коэффициентов корреляции, хранящимися в ЗУ. Обычно аналого-цифровое преобразование производится с невысокой

точностью, результат измерения представляется тремя-четырьмя двоичными разрядами. Количество интервалов квантования корреляционной функции mlOO.

Устройство умножения должно обладать быстродействием, обеспечивающим выполнение т операций за интервал времени At. Если на выполнение операций ум-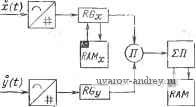

Рис. 12.22. релометра

Схема цифрового кор-

--J J J - .-;;,!; ножения отвести 50 мкс И принять

т=64. то lAmir =3,2-10-3 (, Отсюда видно, что подобный режим коррелометра позволяет анализировать относительно низкочастотные случайные процессы.

Для повышения быстродействия используются режимы работы коррелометра, при которых Д^/то>1. Тогда количество интервалов квантования т уменьшается, упрощается запоминающее устройство RAMx, облегчаются требования (но быстродействию) к устройствам умножения. Однако для обеспечения заданной погрешности оценки корреляционных функций необходимо увеличивать длительность реализаций случайного процесса.

До сих нор рассматривались коррелометры, предназначенные для работы со случайными процессами, реализации которых представлены в виде электрических сигналов. Однако большое количество реализаций может быть дано в виде графических материалов. Известны коррелометры параллельного и параллельно-последовательного действия, выполненные с применением оптических средств восприятия и обработки таких графических материалов. Оптические устройства для статистической обработки графиков позволяют обеспечить высокое быстродействие при относительно невысокой сложности. Для корреляционного и вообще статистического анализа с помощью оптических устройств целесообразно использовать специальные формы представления анализируемого графического материала (теневые графики, кодовая регистрация и т. д.). Для статистической обработки графических материалов весьма широко используются сканирующие ИС.

Корреляционные ИС с измерением коэффициентов многочлена, аппроксимируюиего корреляционную функцию

Оценка корреляционной функции может быть представлена в виде аппроксимирующего многочлена

/?*;,(.)= 2 <,<р,(.).

г оо Г 00

С* = J J{-) 9, {-)dtd.± j yx{t)x{t- .) <p, (т)dtd-z

0 0 0 0

T 00

=yjWj( -)T.(-)rf.rf--

Здесь {фь(т)}-система базисных функций, чаще всего ортогональных.

Нетрудно заметить, что - i)<f,(-)di является откликом

линейного ортонормированного фильтра Ф при подаче на его вход

о

сигнала xit) (рис. 12.23). Следовательно, при применении цепочки ортонормированных фильтров отпадает необходимость в специальных устройствах, создающих запаздывание т. В [12.9] приведены результаты исследования, направленного на создание коррелометров, в которых используется разложение корреляционной функции по полиномам Лагерра. В этом случае ортогональные фильтры должны иметь передаточную функцию

1 I p-a/2\k р + а/2 \ p + a/2j

где р -оператор дифференцирования; а - коэффициент.

Ф

Рис. 12.23. Схема включения ортогонального фильтра

Общий член ортогональной функции Лагерра

а корреляционная функция может быть восстановлена при известных коэффициентах Сп как

Примеры применения корреляционных ИС

Как уже говорилось, корреляционный анализ случайных процессов применяется весьма широко в различных областях науки и техники. В частности, привлекает внимание возможность исполь зования в ИИТ фильтрующих свойств, заложенных в корреляционном анализе, в целях выделения полезных детерминированных сигналов на фоне помех:

Положим, имеются периодический (например, синусоидальный) сигнал u{t) и стационарная случайная помеха y{t), аддитивная по отношению к полезному сигналу и имеющая интервал корреля-

ции тоу. Тогда оценка корреляционной функции x{t)=u{t)-\-y(t}, будет равна:

т

tx (-) - [и (О +1 {t)\ [и it + х) +i (t 4- X)] dt =

г т т т

J и it) и it + т) dt -f f I (t) I [t + x) л + j li {t) I {t x) dt +

+ yy{t)l{t-.)dt

Поскольку сигнал и помехи не коррелированы, то два последних интеграла равны нулю. Следовательно,

При т>тоу/?у*(т>Тог,) 0 и Rx*{х>хоу) Ru*(г).

Таким образом, проведя измерение корреляционной функции при т>тоу, можно отфильтровать влияние помехи.

Значительное уменьшение времени анализа в этой ситуации, может быть получено при применении дополнительного генератора,

о о

повторяющего полезный сигнал %{t)=kLi {t), и измерении

с о

взаимной корреляционной функции процессов x(t) и x{t):. т

R-X. xi-) = ~rj [ (О + yim % it -\-)dt=Ru. X {-) + . X {-) Rv, X {-) о

о

Это устройство с генератором функции %{t), но существу, является аналогом фильтра с узкой полосой пропускания при частотном методе фильтрации. Подобные методы используются в целях уменьшения влияния случайных аддитивных помех в измерительных усилителях, для определения источников шумов (например, в технической диагностике) -и т. п.

Автором [12.8] высказывалась мысль о возможности использования этих методов для построения помехоустойчивых устройств сравнения уравновешиваемых измерительных цепей с параметрическими датчиками, поскольку питание таких цепей имеет известный и детерминированный характер.

Продолжаются применение и разработка корреляционных методов защиты от помех при геофизической разведке полезных ископаемых электромагнитным способом.

Значительный класс статистических ИС - корреляционные экстремальные ИС - основан на использовании наличия особой точки-экстремума корреляционной функции при нулевом значении аргумента [12.11, 12.12]. Корреляционные экстремальные ИС широко применяются в навигации, радиолокации, металлообрабатывающей, химической нромышленности и т. д. для измерения параметров движения разнообразных объектов.

Так, например, известны корреляционные измерители скорости движения горячего и холодного металла при прокатке, судна, самолета и пр.. [12.13, 12.14]. Принцип их работы (рис. 12.24) за-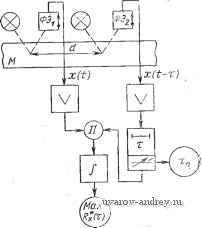

Рис. 12.24. Корреляционный измеритель скорости проката металла

Таблица 12.1. Анализаторы распределения вероятностей, коррелометры

Примечание. А - плотность распределения вероятности амплитуд; В - то же времени между импульсами; Д - то же частот источников импульсов; АА, АВ, АД, ВВ, ВД - двумерные плотности; ЦПМ - цифропечатающая машина.

ключается в том, что имеются два приемника ФЭ и ФЭ2 сигнала отраженного от некоторой поверхности, перемещающихся относительно нее со скоростью v, которую нео-бходимо определить. На выходе приемников будут формироваться зависящие от свойств отражающей поверхности случайные процессы, сдвинутые между собой на интервал времени Ти- Если расстояние между приемниками отраженного сигнала постоянно и равно d, то, измерив т^, можно определить скорость v-d/xn-

Учитывая, что корреляционная функция этих случайных процессов имеет максимум при т=0, имеется возможность изменять запаздывание случайного процесса в канале х(1-х) и добиваться на выходе коррелометра максимального значения коэффициента корреляции, отсчитывая при этом Хп- По данным, приведенным в [12.11], ногрещность измерения скорости движения металла М 36 м/с не превышала 0,1%. Время, необходимое для получения результата измерения, при таких скоростях составляет (при автоматической работе) доли секунды.

Корреляционные экстремальные ИС используются для измерения дальности нахождения объекта в воздухе и воде, т. е. как высотомеры, измерители расстояния между объектами и т. н. Скорость распространения радиоволн в воздухе Со=3-105 км/с, а ультразвуковых волн в воде Сб=1,5-10 м/с. Следовательно, после измерения времени запаздывания сигналов тц (в секундах) можно получить расстояние в воздухе при локации 1,о=С'оТц/2=1,5-10Чц (в километрах) и в воде Lb==.1 500тц/2 (в метрах).

При использовании корреляционных экстремальных ИС для локации космических кораблей удается измерить расстояния порядка 3300 км с ногрешностью ± 1 м, до 2-10 км с погрешностью ±10 км [12.12].

Выделение сигналов на фоне щ-умов, измерение параметров движения, распознавание образов, идентификация, техническая и медицинская диагностика - вот неполный перечень областей практического приложения методики и средств корреляционного анализа.

В табл. 12.1 приведены данные некоторых выпускаемых промышленностью коррелометров.

В настоящее время подавляющий объем корреляционного анализа выполняется корреляционными ИС, содержащими ЭВМ, и локальными устройствами со средствами микропроцессорной техники.

12.4. СПЕКТРАЛЬНЫЕ ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ

Основные определения

Системы спектрального анализа предназначены для количественной оценки спектральных характеристик измеряемых величин.

Напомним основные определения спектральных характеристик [12.13, 12.3]..

Известно, что абсолютно интегрируемые функции, удовлетво-

ряющие условию x(t)dt<:c>o, могут быть представлены в виде интеграла Фурье

Функция S(/со) называется комплексным спектром, или спектральной плотностью амплитуд, и равна:

5ЧН== x{t)e~ dt.

5 (/со) имеет случайный характер, так как соотношения между амплитудами и фазами колебаний различных частот случайных процессов неопределенны. Поэтому при спектральном анализе случайных процессов определяется спектральная плотность мощности (энергетический спектр). Для стационарных эргодических случайных процессов спектральная плотность мощности - математическое ожидание от периодограммы

Т^оа Г

Оценка спектральной плотности мощности

Сх*(сй)=Л1[52(/сй/7].

Необходимо отметить, что в спектральном анализе применяется не только спектральная плотность мощности одного процесса, но и взаимная спектральная плотность мощности реализаций двух процессов.

В соответствии с теоремой Винера - Хинчина энергетический спектр и корреляционная функция связаны между собой преобразованием Фурье:

со 00

Ga:( )= J/?A:(x)exp(-/шх)с?т1= j/?;i:(t)cos<Bx<ix;

-оо -00

Rx (х) =- \ Gx ( >) ехр (/<вх) do) =- I Gx ( )) cos шхш.

2п J J

-00 -30

Проиллюстрируем связь между ?х(т) и Сх(сй) несколькими примерами.

Если /?х(т) является убывающей функцией с увеличением т, то Gx (со) - функция, убывающая по мере увеличения со. Если -/?х(т) приближается к б-функции, то Gjr(cu) -к равномерному белому шуму (рис. 12.25). Если х{() помимо случайной состав-

ляющей содержит периодическую составляющую с частотой ио, то спектральная плотность мощности имеет разрыв непрерывности в точке СОо (рис. 12.26). При т=0

т. е. элемент Gx(cu)dcu определяет составляющую M[x{t)] от комплексной частоты со (рис. 12.27). Таким образом, спектральная плотность мощности описывает частотное распределение средней мощности случайного процесса.

Рис. 12.25. Равномерная спектральная плотность мощности (в) и соответствующая ей корреляционная функция {б)

Рис. 12 26. Спектральная плотность мощности (а) и соответствующая ей корреляционная функция (б)

При спектральном анализе используется выражение для нормированной спектральной плотности мощности:

gx(c))=G*( )/Ox*.

Нормированная спектральная плотность связана с нормированной корреляционной функцией следующим образом: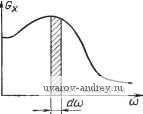

2п

При Т=0

J gx{is>) COS (Bxdco;

Яа:( )= рА:(1)ео8<в1Йт:.

-со 00

JgA:( >)rfcD= 1.

Рис. 12.27. К выделению элемента Gjc(cu)rfw

Методы измерения спектральной плотности случайных процессов

Существующие методы спектрального анализа основываются на применении частотных фильтров или на использовании ортогональных преобразований случайного процесса и преобразова-

НИИ Фурье над известной корреляционной функцией Rx{x). При параллельном фильтровом анализе (рис. 12.28) наибольшее применение получили полосовые избирательные фильтры-резонаторы. На выходе каждого фильтра, пропускающего узкую по-

x(t)

> И

Рис. 12.28. Схема многоканального фильтрового спектрального анализатора

лосу частот сОф, после возведения в квадрат и интегрирования получается составляющая спектра

Gx (о1ф) Dx ( >ф)

2п

Л^(Шф)Ш,

где Л(соф) -частотная характеристика фильтра.

При последовательном анализе используются перестраиваемые фильтры и гетеродинные анализаторы (рис. 12.29). Гетеродинные анализаторы находят большее применение, так как они проще в технической реализации. В них с помощью генератора периодических колебаний с перестраиваемой частотой - гетеродина- происходят последовательный сдвиг частотного спектра исследуемой величины и выделение из него с помощью полосового (обычно резонансного) фильтра составляющих энергетического спектра.

Рпс. 12.29. Схемы спектральных измерительных систем с перестрапвае-мыми фильтром (а) и с гетеродином (б)

Применяются также анализаторы последовательно-параллельного принципа действия.

Разрешающая способность фильтровых анализаторов определяется наименьшим частотным интервалом ДД в пределах которого смежные компоненты спектра различимы и который зависит обычно от полосы пропускания избирательного фильтра, взятой на уровне 0,7 максимального значения его амплитудно-частотной характеристики.

При параллельном анализе время анализа 7пар определяется временем установления колебаний в фильтрах с заданной сте-

пенью приближения амплитуды колебания фильтра к своему максимальному значению Атах=1:

Разрешающая способность и время анализа [12.15] связаны соотношением Д/Д^=Л=соп51, показывающим, что нельзя одновременно улучшать обе эти характеристики.

При последовательном анализе, используемом для выявления составляющих дискретных спектров, время анализа (при полосе исследуемого спектра, равной f) будет равно:

Tnoc=Atf/Af=Af/{Af).

Для уменьшения времени последовательного анализа широко используется изменение частотного масштаба исследуемого процесса, например скорости его записи и воспроизведения, при этом 5и(/сй) =5(/сйй).

Если k>l, то время анализа уменьшается. Для изменения скоростей записи и воспроизведения используются магнитная запись, запоминающие электронно-лучевые трубки, рециркуляционные линии задержки и т. п. Отношение скоростей k от 100 до 10 000 удается получить при анализе квантованных по времени дискретных последовательностей и кодоимпульсных сигналов.

Отечественной промышленностью выпускаются гетеродинные анализаторы спектра серий СЧ и СКЧ и др. [12.6], перекрывающие широкий частотный диапазон исследуемых электрических сигналов (от долей герца до десятков гигагерц).

При проектировании спектральных ИС все в большой мере используются принцип агрегатирования и средства микропроцессорной и иной вычислительной техники. В спектральном анализе все больше используется метод быстрого преобразования Фурье.

Для спектрального анализа одиночных импульсов выпускаются анализаторы параллельного действия с коммутаторами и регистрирующими устройствами (например, АСОИ-1, имеющий 8 каналов, погрешность измерения суммарного значения спектральных составляющих порядка ±20%, время анализа от 300 до 500 мс).

Бесфильтровые методы спектрального анализа в большинстве случаев основаны на определении коэффициентов ряда Фурье. Оценка спектральной плотности мощности при этом может быть получена из выражения

г Т -12

G*x( )--f Ж[5(/.

к {t) cos (otdt

. М[лч< )+вЧ )]-