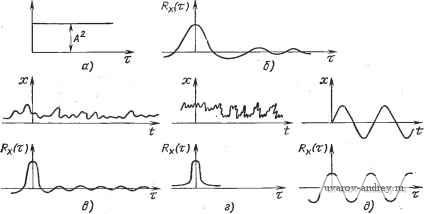Рис. 12.12. Виды корреляционных функций

о - постоянной величины; б - случайной иеличины с относительно большим интервалом корреляции е, г --то же, ио с меньшим по сравчению с предыдущим случаем интервалом корреляции; д - синусоидальной величины

КО формально можно трактовать как случайные процессы. Их используют обычно для проверки коррелометроз.

В прикладном корреляционном анализе довольно часто используется понятие интервала корреляции. Под интервалом корреляции понимается значение аргумента корреляционной функции to, при котором корреляционная функция не превышает некоторого заранее заданного значения е:

I рх (т) I <8 для Т>То.

Используются также определения интервала корреляции через интегральное значение корреляционной функции:

.о

\е для c>V;

J РА:()<е ДЛЯ = =

Выбор того или иного выражения для интервала корреляции определяется характером прикладных задач.

Так, например, интервал корреляции то используется при оценках математического ожидания случайных процессов, то -при определении шага квантования по времени непрерывных реализаций при осциллирующих корреляционных функциях. То - при оценке эффективности оценок корреляционных функций.

Методические погрешности корреляционных измерений весьма подробно рассмотрены в литературе [12.7, 12.8].

Остановимся лишь на тех результатах исследования этих погрешностей, которые необходимы для организации экспериментального определения корреляционных функций.

Погрешность от влияния квантования исследуемой величины по амплитуде оказывается незначительной при относительно невысоких требованиях к точности измерения мгновенных значений. Положим, при квантовании случайного процесса образуется шум квантования n{t). Квантованное по амплитуде мгновенное значение случайного процесса будет равно:

xAt)x{t)-]-Mx-\-n(i).

В этом случае

Rx (-) = М [X,(t) х„(t -f .)] М [1сit) -f х)4- x{t)Мх-ь -f х {() я 4- 1) -f Мхх [t -f- г) -L М'х -Ь Мхп + ) + . fО X

X к (/ -f г) + МхП (t)+ п (t) п {t -Ь т)].

Если квантователь имеет шумы квантования с нулевым математическим ожиданием, то

M[M;fn(/+t)J=0; 7W[Mx (0]=0.

Кроме того, Л1[х(0ад=0 и M{Mxx(t-\-%)]=(). Тогда

Rx, = Rx {-) + М\ -У Rxn (-) + Rnx (-) -г Rn {-)

При интервалах квантования Ах<Хтах можно полагать шум равномерно распределенным, интенсивность шума квантования М[ 2] = /? (0) = (Дл:)712- (т). При Ал:/0<1 взаимная корреляция шума квантования и сигнала x{t) практически может не учитываться. Следовательно, Rx,{:)Rx{:)-\-Mx+{x)/l2. Если не вводить поправку на Rn{x), то оказывается, что относительная погрешность б из-за квантования сигнала по уровню даже при незначительном количестве квантов т имеет небольшое значение. Так, при т = 4 б 20%; т=8 85%, при т=16 6=1,2%, при 7=32 6 = 0,3%, при т = 64 6=0,09%.

На практике в целях уменьшения влияния возможных отклонений математического ожидания и плотности распределения шума квантования от расчетных значений обычно применяют АЦП имеющие от 16 до 64 делений.

При определении оценок корреляционной функции важно учитывать погрешности, обусловленные кснечным временем Т реализации или числом дискрет N случайной последовательности. При проектировании корреляционных ИС приходится решать также задачу определения Т или (V при заданной погрешности.

Эта задача может решаться по-разному в зависимости от полноты априорной информации о виде корреляционной функции, которая должна быть получена в результате измерения.

Положим, известна нижняя частота ю„ гармонических колебаний спектра корреляционной функции. Тогда j 12-8], если ограничиться временем реализации 2Т,

W -cos т - cos со т [Rx (.)].

При заданной погрешности 6t[/?jc(t)J можно определить Т:

Так, например, при бт[?х(т)]=0,02 /Ст>8.

Для эргодического стационарного случайного процесса с нормальным законом распределения и нулевым математическим ожиданием при некоррелированной выборке значений анализируемого процесса может [12.2] использоваться следующее выражение:

D {R*x(-z)\ 1 ---о р =

Если объем выборки ограничивается техническими характеристиками аппаратуры, то можно усреднить результаты измерения, полученные на отдельных участках, и тем самым уменьшить 6(т).

Более подробно эти вопросы рассмотрены в [12.2, 12.4, 12.7, 12.8]. Интервалы квантования Ат корреляционной функции по аргументу выбираются в зависимости от допустимой погрешности восстановления корреляционной функции. На практике при восстановлении корреляционной функции весьма часто используются полиномы невысокой степени (в большинстве случаев - первой).

При линейной аппроксимации и известном значении максимума модуля второй производной IМ I корреляционной функции имеем

LYS\I\M \. Если р;,(т) = е- то Ах = (1/р)]/88;. При Рл: (mfiJ ~ 0,05, т: д; = 3/р количество дискрет нормированной корре. ляционной функции я - З/j/ 88р -- 1. Принимая 5р = 0,02, получаем я = 9.

Обычно для восстановления Rx*(x) с погрешностью около 1 - 2% достаточно на отрезке самой высокочастотной составляющей корреляционной функции взять примерно 10 дискрет, для монотонной по характеру корреляционной функции достаточно взять 10- 15 интервалов Дт, для затухающей по гармоническому закону функции - 30-40 интервалов, для двухчастотных функций - около 100 интервалов и т. п.

Наиболее существенные результаты по анализу аппаратурных погрешностей корреляционных ИС получены в [12.1, 12.2, 12.7]. Остановимся кратко на рекомендациях, полученных в результате этого анализа. В корреляционных ИС даже значительные внешние влияния, если они не коррелированы с исследуемыми процессами.

мало сказываются на результатах измерений. В то же время небольшой дрейф характеристик или возникновение помех, коррелированных с x{t), может вызвать появление значительных погрешностей.

Степень влияния помех и погрешностей существенно зависит от места их возникновения в системе. В частности, центрирование случайных величин целесообразно выполнять на входе, а не на выходе ИС.

Точность корреляционных ИС во многом определяется их принципом действия. Цифровые ИС имеют в этом смысле большие преимущества, при этом их сложность относительно невелика.

Следует выделить два основных метода построения корреляционных ИС. Первый из них связан с измерением коэффициентов корреляции и последующим восстановлением всей корреляционной функции, второй - с измерением коэффициентов многочленов, аппроксимирующих корреляционную функцию.

По каждому из этих методов система может действовать последовательно или параллельно, работать с аналоговыми или кодоимпульсными сигналами, в реальном времени или с изменением скорости и т. п.

Корреляционные ИС с последовательным измерением коэффициентов корреляции

Рассмотрим методы построения систем, в которых выполняются прямые (некомпенсационные) измерения коэффициентов корреляции.

Среди них наиболее распространен метод умножения. При его реализации используются формулы

т

?*х() = Гх(0(+-)й;

о

г

при фиксированных значениях аргумента Мт, k=0, 1, 2 ... На рис. 12.13 и 12.14 показаны схемы аппаратной реализации для измерения коэффициентов корреляции корреляционной и взаимно корреляционной функций. Поскольку метод умножения применим для корреляционного анализа любых стационарных случайных процессов, то большинство корреляционных ИС построено на его основе.

Имеются решения, позволяющие избежать операции умножения. Они связаны в большинстве случаев с заменой умножения возведением в квадрат суммы значений х и х (t+x).

Для стационарных случайных процессов

M[x(l)+x{t+r)y = 2DxU+px{x)];

. M{[x{t}+x{t+T)V-[x{t)-x(t+rm =

=M[4x\t)x\t+T)]==4Rx{T).

Нужно, однако, заметить, что коррелометры, основанные на таком принципе действия, не имеют преимуществ по точности перед коррелометрами с умножением, а выигрыш по простоте реализации сомнителен.

x{t)xaft)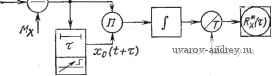

Рис. 12.13. Схема, реализующая метод умножения при измерении дискрет корреляционной функции

x(t)

Xo(t)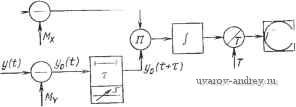

Рис. 12.14. Схема, реа-fxrWl лизующая метод умножения при измерении взаимно корреляционной функции

Коррелометры, построенные по полярному методу (методу зна-косочетаний) [12.8], являются наиболее простыми, но они применяются для анализа центрированных нормальных стационарных случайных процессов. Двумерная плотность распределения нормального случайного процесса

27xo]/l-f=(x)

ехр

- 2xiX2?(c) -f Х^а

2oM1-pV=)]

где xi==a:(0; 2=-<(+)) определяются значениями нормированной корреляционной функции. Следовательно, если найти совместную вероятность некоторых значений х{1) и х(+т) [или г/(+т)], то можно определить рх(т). Наиболее просто находятся вероятности совпадения (или несовпадения) знаков случайных процессов (рис. 12.15), сдвинутых относительно друг друга на интервал т [12.2]:

Р++ (t) =Р- (т) (1 / 2л) arccos [-р (т) ]. Отсюда р (т) =-cos 2я [р++ (т) ].

Структурная схема полярного коррелометра относительно проста (рис. 12,16). Однако необходимо принимать меры по обеспечению одинаковых частотно-фазовых характеристик каналов, исключению связи между ними, уменьшению дрейфа нуля во входных цепях и т. д. Выпускаемый серийный полярный коррелометр КА-ЗД имеет погрешность не более 10%, частотный диапазон от 50 до 20 ООО Гц и динамический диапазон сигналов 100 мкВ - 3 В.

При релейном методе используются формулы

Гх () =М[х (/) sign X {t -{-.)] = Vh °хРх (-t);

Rx. Y (т:) = М [К (t) sign y{t-]- 1)]= y2jiz OxPx. Y (=)

Коррелометры, основанные на релейном методе ( значение - знак ), обладают более высокой точностью по сравнению с полярным коррелометром и приближаются в этом смысле к коррелометрам, основанным на методе умножения. Следует отметить, что при релейном методе объем выборки увеличивается примерно в 2 раза по сравнению с методом значение - значение и определяется из следующего выражения: бр=(1/Л^нк) {[jxV4px(t)] - 1},. где Л'нк - количество некоррелированных значений исход'юй функции. Имеются исследования, направленные на повышснпе точности полярного и релейного методов путем введения вспо.\.игательных-случайных сигналов и т. п.

При измерении коэффициентов корреляции с применением интеграла Стилтьеса используется аналого-цифровой принцип построения коррелометров в соот- ветствии с выражением

Рис. 12.15. К определению совпадения

о в

знаков x{t) и x(i-)-T)

О

I X, sign X

Рис. 12.16. Схема полярного коррелометра

в этом случае предусматривается, что производится аналого-цифровое преобразование сигнала y{t-{-x). При равномерной шкале АЦП (A=const) можно принять, что Zy{t-{-x)=jAy. Следовательно,

t, t, т

/о

В соответствии с этим выражением структура коррелометра (рис. 12.17) состоит из схемы переменной задержки по времени

сигнала y{t), простейшего АЦП, элементов И и устройства инте-

y(t)

>-4

>

Рис. 12.17. Схема коррелометра, основанного на использовании интеграла Стилтьеса

грирования, на которое сигналы подаются с соответствующими весами, определяемыми значениями сопротивлений R. Количество элементов И равно количеству уровней квантования и обычно невелико (до 10).

СЛСА для рис. 12.17 можно записать в следующем виде:

<р(г, г = 0) Ф(В) \\x{t)\\y{t,-\-.)\\l\y{U-.)lz,{t-\-.)ULy\X

i\y{i-\-)M-\-) = \M

X >[y(-f .):5ЛДг/±Дг 2]1

S:j,J{t)dt-\-uK{t)dt ...Ф(Е).

Верхние пределы некоторых интегралов отсутствуют, поскольку интегрирование х(0 по этому алгоритму производится в течение

о

интервалов времени, пока y{t-\-x) находится в пределе соответствующего уровня квантования с весами, определяемыми этими уровнями. Для реализации этого алгоритма следует схему на рис. 12.17 дополнить устройством, определяющим необходимость выполнения нового аналого-цифрового преобразования.

Одним из наиоолее простых методов получения коэффициентов корреляции является метод диаграмм рассеяния [12.8]. Он пригоден для анализа случайных процессов, подчиняющихся нормальному закону распределения. Основан он на том, что сечения нормальной плотности распределения (при заданном т) представляют собой эллипсы, отнощение главных полуосей а и b которых определяет нормированную корреляционную функцию

р^,у(т) = [1-(а/.6)2]/[1--(а/6)2].

Фигура Лиссажу, получаемая с помощью электронного осциллографа, обычно имеет размытый вид. Для измерения а и 6 выбираются линии равной яркости. Подобный метод пригоден для ориентировочной оценки значений коэффициентов корреляции.

Компенсационные методы измерения коэффициентов корреляции разработаны значительно слабее. Однако известные достоинства этих методов, связанные преимущественно с возможностью исключения ряда ногрещностей, заставляют обратить внимание на те немногие попытки, которые направлены на создание компенсационных коррелометров.

Первая попытка создания компенсационного коррелометра была предпринята в 1958 г. [12.10].

в компенсационном коррелометре этого типа изменяется мае-

о

штаб x{t) в а раз (рис. 12.18). Следовательно, на выходе вычит

о о

тающего звена получается сигнал а:(-1-т)-ax{t). После возведения в квадрат (Л'е) и интегрирования получается

М [x{t+x) -ax{t) ] Dx [ 1 +а^-2арх (т) ].

Р1зменением а достигается минимум этого выражения. При этом учитывается, что [l-l-a-2apjf(т)]/da=0, а=рх{%). Погрешности выполнения операций возведения в квадрат и интегрирования в таком коррелометре не оказывают существенного влияния, а требования к указателю существенно упрощаются, так как определение р(т) практически не зависит от знания точного значения минимума, равного Dx\}-р^х-(т)]. Видимо, этот метод не получил широкого распространения ввиду трудностей, связанных с выполнением операций минимизации выходного сигнала, на что требуются определенные затраты времени, и ввиду зависимости уровня минимума от значения сигналов.

Для независимого измерения коэффициентов корреляции можно использовать квазикомненсационную цепь, предложенную К. Б. Ка-рандеевым и Г. А. Штамбергером и изображенную на рис. 12.19. На

о о

устройство умножения подаются напряжения й()/2и(и ()/2)Х

о

y(Zv.lz) -и(-1-т), а показывающий прибор реагирует на

Ш[ 2 (О z /z- (О и (-f т) ] =

= [Z) Zk/Z-/? (т)], , ,

где k - коэффициент пропорциональности.

Изменяя 2k, можно добиться нулевого показания индикатора. При этом справедливо соотношение

ри (т)=гк/2.

Благодаря использованию скалярных режимов измерения процесс уравновешивания измерительной цепи осуществляется весьм.а просто и может быть автоматизирован. Время проведения эксперимента практически будет определяться временем, необходимым для выполнения операции осреднения. Схема, реализующая этот принцип, успешно использовалась в аппаратуре для геодезической аэроэлектроразведки методом естественных электромагнитных полей.

xft)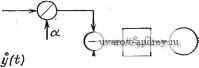

S(t)

z/2 Z/Z

Рис. 12.18. Схема с минимизацией выходного сигнала коррелометра

Рис. 12.19. Схема компенсационного коррелометра

Имеется возможность измерения с помощью такого же метода так называемых мнимых коэффициентов корреляции при использовании специальных спектральных фазосдвигающих цепей, обес-

о

печивающих изменение фазы каждой составляющей спектра u{f) в заданном диапазоне частот на угол зх/2 без изменения исходных амплитуд.

Корреляционные ИС с параллельным и параллельно-последовательным измерением коэффициентов корреляции

Преимущества и недостатки ИС параллельного действия присущи и корреляционным ИС параллельного действия.

Структурные схемы аналоговой и аналого-цифровой корреляционных систем параллельного действия представлены на рис. 12.20 и 12.21. Схема аналоговой системы не требует пояснений. Аналого-цифровая корреляционная ИС, описанная в [12.2], позволяет произвести одновременное измерение 100 коэффициентов корреляции. Частота работы генератора импульсов от 100 Гц до 1 МГц, максимальное время задержки создающейся регистрами сдвига, при этом изменяется от 1 с до 100 мкс. Кодоимпульсный сигнал от АЦП поступает сначала на триггерные регистры сдвига, затем на умножающие устройства и на интегрирующие цепочки. Измерение уровней напряжений на конденсаторах производится после выполнения цикла анализа.

x(t)

Рис. 12.20. Многоканальная аналоговая корреляционная ИС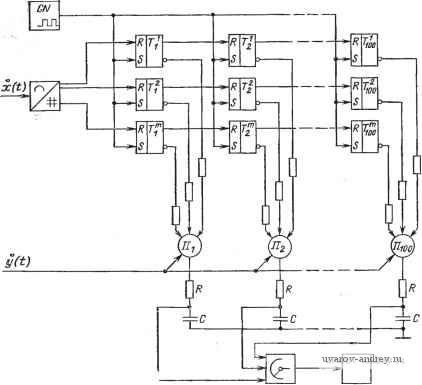

Рис. 12.21. Многоканальная аналого-цифровая корреляционная ИС

В цифровых коррелометрах параллельно-последовательного действия возможно несколько вариантов структур. В большинстве случаев общими элементами информационного канала являются устройства умножения, суммирующее и ЗУ.

Корреляционная функция в цифровом корреляторе при сильно