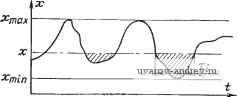Рис. 12.2. Функция распределения вероятностей:

и - к определению функции распределения вероятностей; б - вид функции распределения вероятностей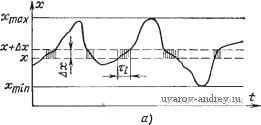

так

Рис. 12.3. Плотность распределения вероятностей:

о - к определению плотности распределения вероятностей; б - вид плотности распределения вероятностей

Двумерный интегральный закон распределения вероятностей стационарного случайного процесса x{t) определяется вероятностями нахождения x{t) и x{t-\-x) ниже уровней х\ и xi:

F{xu Х2, t)=p[x(0<x,; x(+t)X2].

Одно- и двумерные дифференциальные законы распределения вероятностей случайного процесса x{t)-плотности распределения вероятностей (рис. 12.3)-определяются следующими выражениями:

f{x)=dF(x)/dx; f{xi, х^, т) =

=dF{Xi, Х2, x)/dxidx2 или ,

f (х)dx=p[xx{t) x+dx];

f(Xb X2, x)dxu dX2 = p[Xi.x{t) Xi-\-dXi; X2x(f+t)X2±rfX2].

Определение вероятностей p[x{t)x] и p[xx{t) x+dx] можно производить путем суммирования отрезков времени, в течение которых выполняются указанные неравенства, и отнесения полученной суммы к времени наблюдения:

для функции распределения

Т-*оо Т

для плотности вероятности

St.-

f{K, Ах) = lim

г^оо Т Дх

Если исследуемый процесс представлен решетчатой функцией (в виде дискрет, размешенных через интервал дискретизации At), то выражения для интегральной функции и плотности распределения примут следующий вид:

F{x, N, ДО = lim

Л/->=о

f{x, N, М, Дх:) = Ит

В этих выражениях At-интервал дискретизации; п-количество дискрет, уровень которых меньше х для функции распределения или находится в интервале х+Ах для плотности распределения; N=T/At-количество дискрет в исследуемой реализации-объем выборки.

В большинстве случаев Д^ равно или больше интервала корреляции исследуемого процесса.

Для определения функции и плотности распределения должен быть получен ряд значений F{x) и f(x, Ах) в пределах динамического диапазона исследуемого процесса. Для этого динамический диапазон разбивается на несколько интервалов квантования и для каждого интервала квантования определяются значения F и f.

При экспериментальном определении закона распределения вероятностей неизбежно возникают методические погрешности обусловленные конечной длительностью наблюдения (7<;оо) или выборки (yV<oo) реализаций и конечным значением интервала квантования по уровню АхфО. Именно ввиду наличия в первую очередь методических погрешностей в результате измерительного эксперимента получаются не точные, а приближенные выражения-оценки законов распределения вероятностей:

F(X. Т)=; Г(х:. Дх:, .

Т йх

Fv, N, Ы) = ;

iif 1

f (л-, N, At, Ах) =

N Дх

Определение интервала квантования по параметру х производится известными способами. В зависимости от степени аппроксимирующего многочлена в теории вероятностей различают представление плотности распределения гистограммой (приближение на интервалах квантования степенным многочленом нулевой степени) или полигоном (приближение многочленом первой степени).

Неравенства Чебышева [12.5] позволяют при заданной погрешности оценки законов распределения приближенно определить время наблюдения при некоррелированной выборке, когда интервал квантования At равен или больше интервала корреляции;

p[max\F{x, Т) -F{x)\b,]-

р [шах I /* {х, Ах, T)Ax-f (х) Д v в,]

Более точное определение времени анализа Т или объема выборки N (при некоррелированной выборке) может быть выполнено, если задана относительная средняя квадратическая погреш-ость измерения а в фиксированных точках F*{x) и f*{x, Ах) по формулам [12.2, 12.5]:

1 -f*(x)

eff(x, Дх) affix, Ax)Ax

Приближенные значения Np и Nf получены при условиях F*(x)l uAxf*{x, AxXl.

Если между выборочными значениями имеется корреляционная связь (Д^<;то, где то-интервал корреляции), то объем выборки нужно увеличить.

Поскольку F*(x, Т) и f*(x. Ах, Т) связаны между собой известными зависимостями, то в статистических анализаторах, видимо, можно ограничиться только измерением F*{x, Т) или f*{x, Ах, Т). Аппаратурные решения для измерения F*{x, Т) проще, чем для f*{x. Ах, Т). Однако большинство ИС делается для измерения плотности распределения. Это объясняется тем, что при преобразовании плотности распределения в функцию распределения погрешности получаются существенно меньшими, чем при обратном преобразовании [12.6].

Рассмотрим основные структуры и алгоритмы ИС, измеряющих дискреты функций или плотностей распределения вероятностей. Такие ИС (будем называть их анализаторами вероятностей) могут быть одноканальными и многоканальными.

Одноканальные анализаторы вероятностей за цикл анализа реализации x{t) позволяют получить одно дискретное значение функции или плотности распределения исследуемого случайного процесса. Для получения всех дискретных значений, необходимых

для представления законов распределения, следует последовательно изменять X или месторасположение интервалов квантования-по уровню Да: и производить измерение величин F*{x и /*(л:г, Дх). Естественно, что при последовательном измерении всех дискретных величин и f* на проведение анализа затрачивается большое время.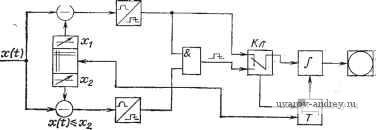

Рис. 12.4. Анализатор с ШИМ и аналоговым интегрированием {х, и Хг-уровни; анализа)

Рис. 12.5. Одноканальная система для измерения функции распределения вероятностей

Е

Рис. 12.6. Система с телевизионным датчиком ТД для измерения распределения вероятностей

Структурные схемы одноканальных анализаторов представлены на рис. 12.4-12.6. Наиболее часто в одноканальных анализаторах, оперирующих с непрерывными сигналами и основанных на измерении относительного времени пребывания процесса x{t), используется образование ШИМ-сигналов и их интегрирование в течение времени Т.

Логическая схема алгоритма анализатора вероятностей, изображенного на рис. 12.4 и настроенного на получение дискрет ПЛО1Ч0СТИ распределения вероятностей, охватывает:

начальное состояние: Ф(В) ([х\; х^; Кл{1)] 1[л:(01Х; образование ШИМ-сигналов: X{I[a:(0<-*i/ o; Д<(л:1)] II

xz/uo; At{x2)]}X;

формирование дискреты плотности распределения: X MlC-i) -

~ut{x,)]; и,} I

1>[М (х,) - М (х,)]; ujr [х„ Дх] I [8:Г(х: Дл;)]Ф(Е).

Разрешающая способность таких анализаторов определяется .дрейфом уровня амплитудных селекторов и формой импульсов. Она обычно ограничивается примерно 1/20-1/100 частью максимального значения измеряемого напряжения.

Если исследуемый процесс представлен в квантованном по времени виде, используются амплитудный дискриминатор с изменяемым уровнем сравнения х (рис. 12.5) и суммирующие счетчики, на выходе которых получаются значения п и 7V.

СЛСА такого анализатора вероятностей:

начальное состояние: ф(л;; N=Q\ п=0; /=0;)Х;

-формирование л:,- и х: X Ф(/ : =/+1) l{xj \\ л:)Х

счет суммарного количества дискрет / и i (с уровнем Xjx): X{I(S:D/) II \l{CR:xux) (>(х^х) I(S:Di]}X;

выдача информации: x (/=jV) [I(Zi) /(Of)] Ф(Е).

Здесь /-текущее суммарное количество всех дискрет проанализированной части исследуемой реализации, а i-текущее количество дискрет с амплитудой, меньшей или равной уровню анализа х.

На рис. 12.5 показан анализатор, предназначенный для измерения F* {х). Предоставляем читателям возможность составить схему и алгоритм анализатора такого типа, позволяющего произвести .измерение f * {х, Ах).

По такому принципу работают одноканальные анализаторы лмпульсов АИ-3-АИ-8, обладающие высоким быстродействием !(до 10 имп./с), повышенной чувствительностью (максимальное значение амплитуды исследуемых процессов до 3-10 в).

Простотой и высоким быстродействием отличаются анализаторы с преобразованием исследуемого временного процесса x{t) в лространственный сигнал х{1). Это преобразование может быть осуществлено с помощью электронного осциллографа при подаче ла отклоняющие пластины электронно-лучевой трубки исследуемого процесса и несинхронного развертывающего напряжения. Возможно также использование оптичесгих систем с перемещаю-л],имися диафрагмами и фотоэлектронным воспринимающим и интегрирующим устройством либо промежуточное преобразование с ломощью телевизионного датчика ТД (рис. 12.6) с последующим анализом полученного потенциального изображения.

Многоканальные анализаторные системы, позволяющие получать законы распределения амплитуд импульсов и интервалов Бремени между ними, амплитуд непрерывных временных и рас-лределенных в пространстве случайных процессов и т. п., широко используются в ядерной физике, биологии, геофизике, в химическом и металлургическом производстве.

Наиболее часто реализации исследуемых процессов представ-.ляются в виде электрических сигналов и графических изображений. Как в том, так и в другом случае могут быть использованы лналоговые, цифровые и смешанные принципы построения анализаторов.

в аналоговых анализаторах используются дискриминаторы, выделяющие каналы-интервалы значений измеряемых величин.

аналоговые накопители (индивидуальные для каждого канала) и устройства вывода (рис. 12.7). В качестве амплитудных дискриминаторов могут использоваться пороговые устройства (типа триггеров Шмитта), фотоприемники с диафрагмами, выделяющими каналы, и т п Обычно при использовании дискриминаторов число-каналов не превышает 30-50. Для накопления данных в этом случае часто используются конденсаторные устройства.

x[t,l)

+ I

о

x(t,l)

Рис. 12.7. Многоканальная аналоговая система для измерения распределения вероятностей

Рис. 12.8. Многоканальная цифровая система для измерения плотности распределения вероятностей

RAM,

RAM,

Рис. 12.9. Структурная схема ИС типа АИ

Структура многоканальных цифровых анализаторов вероятностей (рис. 12.8) включает АЦП, у которого каждое деление шкалы связано с индивидуальным счетчиком.

В многоканальных анализаторных ИС типа АИ, предназначенных для статистического анализа импульсов [12.5J, используются в качестве интегрирующих устройств магнитные устройства памяти (рис. 12.9). Результат измерения в виде кодоимпульсного сигнала I(2j) в таких ИС поступает в регистр RG и определяет адрес ячеек памяти Adz,-, в которых накапливается количество значений исследуемой величины, соответствующих каждому результату измерения. С помощью RG\ к числу, хранящемуся в ячейках памяти данного интервала АЦП, после поступления очередного результата измерения добавляется единица. Промежуточные ЗУ (на магнитных лентах, перфолентах, перфокартах и т. п.) используются для увеличения объема выборки, уменьшения потерь информации и т. д.

Весьма удобной для построения многоканальных анализаторов является мультиплицированная структура (рис. 12.10), пригодная для оценки параметров законов распределения как случайных величин, так и случайных функций. Здесь число ступеней выходного

напряжения Uk ЦАП (число ступеней развертки ) равно числу интервалов группировки f*{x) или F*{x); при этом на каждом такте Ик проводятся определение числа сработавших устройств сравнения и запись этого числа в соответствующие сумматоры, количество которых равно числу ступеней Uk. Если определение числа сработавших устройств сравнения осуществляется путем опроса, то в качестве сумматоров можно использовать обычные счетчики. В зависимости от того, сбрасываются или нет каналь-

Значение/

Рис. 12.10. Мультиплицированная система для измерения распределения вероятностей

ные триггеры в конце каждой ступени, будет измеряться \*{х) или (х). Анализаторные ИС позволяют получать законы распределения амплитуд А, временных интервалов В, номеров источников информации Д в различных сочетаниях (обычно не превышающих трехмерного): А, В, АА, AAA, АВ, ААВ, ВВ, АД, ВД.

Для получения й-мерных законов распределения ИС содержат соответствующее количество АЦП и промежуточное ЗУ (на рис. 12.9-RAM.{). При этом основное запоминающее устройство RAM.2 разделяется на k частей.

В Советском Союзе разработаны и выпускаются анализаторы импульсов типа АИ. Отечественные промышленные анализаторы АИ-128-1М (А), АИ-256 (А, В, Д), АИ-1024 (АА, В, АД), АИ-2048 (А, В, АВ), АИ-4096 (АА, ВВ, АД, ВД) имеют число каналов, равное соответственно 128, 256, 1024, 2048 и 4096, число уровней квантования по амплитуде от 100 до 512 (в АИ-4096-3-А6-до 4096), ширину временных каналов от 10 до 64-10-е с, число каналов координат датчиков от 8 до 100, емкость каналов от 10* до 10 бит, цикл сортировки от 10 до 56 мкс.

Анализаторы АИ-4096-3 и А-2048-1 выполняют дополнительные операции обработки сигналов: сглаживание, нормирование, разложение на элементарные компоненты и т. п. Для этого анализаторы имеют арифметические устройства и устройства управления, позволяющие производить помимо основных арифметических one-

раций операции сравнения, модификации адреса, условного пере-

Анализаторы типа АИ выпускаются в блочном исполнении. К отдельным блокам, входящим в состав современных анализаторов АИ, относятся АЦП, ЗУ, - АЛУ, управляющие, выходные устройства, устройства коммутации и передачи информации. Принцип их действия и технические характеристики изложены в [12.5].

x(t)

Функцио-напьный преобразователь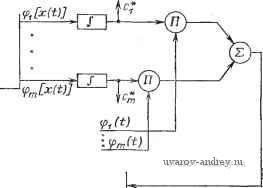

f(X)

Рис. 12.11. Система для измерения распределения вероятностей с аппроксимацией

Для контроля правильности функционирования АИ и определения их характеристик используются генераторы образцовых потоков импульсов. Разработаны генераторы точных амплитудных значений, распределенных, например, по нормальному закону, генераторы белого щума и т. п. Предусмотрен контроль входных и выходных устройств АИ. Разработаны тестовые программы, служащие для проверки работоспособности узлов обработки информации АИ. В [12.5] приводятся данные измерительных комплексов и центров, в которых с помощью коммутаторов и согласующих устройств объединяются для совместной работы несколько АИ и ЭВМ.

Следует отметить, что при работе АИ возникают специфические погрещности, которые следует учитывать. Для этого используется аппарат теории массового обслуживания.

Структура АИС, позволяющая получить коэффициенты многочлена, приближающего кривую плотности распределения вероятностей, представлена на рис. 12.11.

Если учесть, чтоЛ1[х;(0]= J K{f)\{x)dx, коэффициенты раз-

ложения Фурье функции Сд, = J (f [х (Щ dx, а =

=2 k?k[i]. то можно принять, что Cr=M{f,[x{t)]} [12.2].

Сигналы на выходе фильтра (pkit) ортогональны и зависят от времени, а на выходе функционального преобразователя fPk[x{t)]-от исследуемого процесса.

Для графического представления необходимо, чтобы время было связано с уровнем сигнала. Интервал между импульсами 6(0 при определении Ck должен быть больше времени усреднения.

Порядок приближения т может быть определен из анализа средней квадратической погрешности оценки:

о==. nx)dx~ S c,

-оо /г=1

При получении f* (х) описанным методом отсутствует необходимость квантования процесса по времени, могут быть сокрашены емкость используемой памяти и время измерения.

из. КОРРЕЛЯЦИОННЫЕ ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ

Основные определения. Методические погрешности

Для эргодических стационарных случайных процессов выражение корреляционной функции может быть записано как

г

(.) М[х it) °x{t-\- .)] = lim -1- Г {t) x{t +.) d

Г-*оо Г J

о

Аналогичным образом определяется взаимная корреляционная функция двух эргодических стационарных случайных процессов:

т

RxY () \\т^\х (О У it -V ) dt.

О

Иногда под корреляционной функцией понимают

т

RM,x{)-lim- x{t)x{t)dt = Rx{-) + Mx.

Т-*оо J J О

В этом случае корреляционная функция случайного процесса содержит информацию и о математическом ожидании процесса.

Экспериментальное определение корреляционной функции в большинстве случаев связано с измерениями значений корреляционной функции при различных фиксированных т(0т<со). Отдельное значение корреляционной функции при данном т носит название коэффициента корреляции. При т=0 коэффициент корре-

ляции i?x(0)=£x. При т-оо коэффициент корреляции для эргодических стационарных случайных процессов стремится к 0. Для 0<т<оо Rx{t:)Dx. Корреляционная функция является четной функцией своего аргумента, т. е. Rx{x)=Rx{-т).

В результате измерений получаются оценки математического ожидания и коэффициентов корреляции, которые для непрерывных случайных процессов и случайных периодических последовательностей имеют следующий вид:

7- J

x{t)dt;

=1

i = \

Корреляционная функция случайного процесса, отнесенная к его дисперсии, носит название нормированной корреляционной функции рх(т). По определению 0:<рх(т)1.

Проиллюстрируем вид корреляционной функции несколькими примерами (рис. 12.12), взятыми в [12.9]. Корреляционная функция процесса x{t) =А

Rx(x)=A (рис. 12.12.а).

По мере уменьшения статистической связи между ординатами реализаций случайного процесса (рис. 12.12,6, в) корреляционная функция приближается к дельта-функции. Для нормального белого шума корреляционная функция описывается дельта-функцией (рис. 12.12,г).

Для синусоидального процесса корреляционная функция равна -Rx(t) = (/42/2) cos ют (рис. 12.12,(3). Нужно заметить, что величины, имеющие постоянное значение или периодический характер, толь-