Для г-го компонента смеси в этом случае решение может быть найдено в следующем виде:

Xi=a,o-f-fl-iZi-fa,-2Z2-fa,-3Z3-Laiii2i2-fai2222+ai33Z32--fl.i2ZiZ2+aii3ZiZ3-f

+а,-2з222з--а,-11 iZ2-f~*222Z2-H 33Z3+ 1122lZ2-)-ai223Z2Z3~)-+anse2lZ2-faii33ZiZ32-j-ai233Z2Z32-f-ai22322Z3-f-ail232iZ2Z3.

в реализованной на этом принципе действия контрольно-измерительной системе параллельно-последовательного действия выполняются измерение и контроль состава трехкомпонентных растворов глиноземного производства в 15 сечениях технологической линии за время, не превышающее 2 мин.

Для анализа состава многокомпонентных сред широко используется также измерение реакции среды на электромагнитное многочастотное воздействие.

Такой метод анализа получил название многочастотного. Известны его применения для измерения физико-химических свойств стали, влажности зерна и т. п.

Перейдем к краткому изложению сути другого метода раздельного измерения зависимых величин, который назовем условно методом моделей. Этот метод весьма полно исследован и давно используется в электроизмерительной технике для раздельного измерения активной и реактивной составляющих комплексных сопротивлений и напряжений [11.4, 11.5]. Действительно, в самом общем виде мосты и компенсаторы переменного тока содержат модель измеряемого объекта (сопротивления или напряжения), известные параметры которой сравниваются с неизвестными параметрами объекта. При достижении определенных соотношений между ними (в равновесном режиме - равенство этих параметров) результат измерения определяется по известным параметрам модели.

Мостовые и компенсационные схемы переменного тока являются вариантами реализации метода структурных моделей, используемого для раздельного измерения зависимых величин. На объект исследования и модель объекта (рис. 11.2) подается внешнее воздействие. Реакции объекта Хг и модели Хг* сравниваются, затем параметры модели изменяются до тех пор, пока между ними и параметрами объекта не будут выполнены определенные соотношения. Метод структурных моделей применительно к раздельному измерению составляющих сложных электрических цепей осуществляется в многомерных электроизмерительных устройствах сравнения.

В [11.6] обобщены основы построения, исследованы вопросы чувствительности, сходи-мости и устойчивости процессов уравновешивания при применении итерационного метода, произведен анализ погрешностей многомерных электроизмерительных устройств сравнения. Кроме того, приведены данные о разработанных устройствах для измерения и контроля элементов радиоэлектроники, сеточной модели и т. д.

На рис. 11.3 показана схема измерения сопротивлений Ri, R2, R3, Ri, сходящихся к узлу О сеточной модели с помощью многомерного устройства. В момент равновесия

Ri=R iR./Rc; Rs=RiRa/Rc; RsRsRa/Rc; RiRafRc

На эти соотношения не оказывают влияния остальные сопротивления сеточной модели.

{Xi)n

Модем объекта

Внешнее воздействие

Рис. 11.2. Структурная схема устройства с моделью объекта

Рис. 11.3. Измерение сопротивлений сеточной модели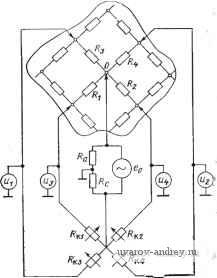

[А

r~\-i til Mi МгГ^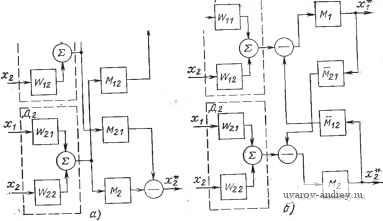

Рис. 11.4. Структурная схема ИС с прямыми (а) и обратными (б) перекрестными связями

Следует отметить, что при числе контуров уравновешивания, превышаюшем? два, схемы и алгоритмы для раздельного измерения зависимых величин существенно усложняются. Для автоматического уравновешивания в многомерных измерительных устройстиах используются методы наискорейшего спуска, градиента, Гаусса - Зейделя, описанные в гл. 8.

Задачу разделения взаимосвязанных величин в ряде случаев можно решить используя введение искусственных перекрестных связей, учитывающих неселек-тивиость датчиков или взаимосвязь измеряемых величин в среде. На рис. 11.4,а представлена структурная схема системы, предназначенной, для раздельного

измерения двух величин, в которой используются прямые связи, а на рис. 11.4,6- обратные связи. На этих рисунках W - передаточные функции датчиков, М - людели датчиков, Д, и Да -датчики.

Для случая разделения двух переменных (рис. 11.4) прямые перекрестные связи Mi2=MiWi2/W22 и M2i=M2lF2i/Wii, а обратные связи Mi2=(l/M2)X X(Wi2/W22) И M2i=(l/Mi) (U72i/U7,i). Результирующие передаточные функции ло каждому каналу определяются для схемы на рис. 11.4,а в виде

Я, = М, U7 (1 U7,2 U72,/U7 U722) ;

H2==M2W22(.l~Wi2W2l/W2lW2>2),

a для схемы на рис. 11.4,6

Hi=MiWu; H2=M2W22;

Из этих выражений видно, что с помощью введения перекрестных связей можно осуществить не только разделение сигналов, но и их функциональное преобразование.

Если выбрать Mi = l/U7 , и M2=l/W22, то работа второй схемы сводится к так называемому методу обратных операторов.

Известно применение метода перекрестных связей для уменьшения взаимного влияния компонентов в четырехкомпонентных аэродинамических весах с упругими элементами и тензодатчиками. При этом удавалось примерно на порядок уменьшить взаимное влияние компонентов.

Методы перекрестных связей и обратных операторов можно отнести к не-.посредственным методам разделения и измерения зависимых величин, а метод .структурных моделей - к компенсационным методам.

Видимо, возможно совместное использование метода перекрестных связей, юбеспечивающего относительно простое разделение величин, и метода структурных моделей, обладающего, в принципе, лучшими возможностями по точности .измерения. По сути дела, в таких системах используется комбинированное управ--ление по разомкнутому и замкнутому каналам с применением принципа инвариантности (компенсации) системы к внешним возмущениям.

11.2. АППРОКСИМИРУЮЩИЕ ИС

Если нужно количественно оценить и при необходимости восстановить исход-яую входную величину, являющуюся функцией некоторого аргумента, то имеется -Принципиально два пути выполнения измерений. Первый, чаще используемый, .заключается в измерении дискрет этой величины, расположенных через опреде-.ленные интервалы аргумента, и восстановлении ее путем аппроксимации с помощью многочленов невысокой степени. Второй путь связан с измерением коэф- фициентов многочленов, аппроксимирующих исходную функцию на всем интерва--ле ее анализа. Естественно, что порядок аппроксимирующего многочлена при этом должен быть более высоким. Нужно отметить, что при соответствующем .выборе типа приближающего многочлена имеется возможность не только количественного описания поведения изучаемой величины в любой точке интервала яаблюдения, но и одновременного получения информации о некоторых свойствах этой величины. В частности, при использовании ряда Фурье знание коэффициентов ряда позволяет судить о частотном составе изучаемой функции.

Измерительные системы, позволяющие измерять коэффициенты, приолижа -щих многочленов, далее называются аппроксимирующими (АИС). Подчеркнем что АИС относятся к системам, предназначенным для количественного описания величин, являющихся функциями времени, пространства или другого аргумента и их обобщающих параметров, определяемых видом приближающего многочлена.

Коэффициенты аппроксимирующего многочлена зависят от изучаемой x{t) и выбранной системы приближающих функций ф(/). Получение коэффициентов, многочлена, аппроксимирующего исходную функцию,

Ch=F,[x(0, фПО].

относится к области анализа сигналов. Эта зависимость при равномерном кван-

товании по аргументу имеет вид Ck= x(tj)((ihiti), где /=1, 2, ..., N - по

рядковый номер дискретных значений исходной функции x{t).

Заметим, что наиболее часто изучению подлежат процессы x{t) и пространственные функции х{1).

Кроме времени и пространства в качестве аргумента в АИС употребляются-интервалы корреляции при описании корреляционной функции, частоты при описании спектральных характеристик и т. д. (рис. П.5).

Для восстановления (синтеза) исходной изучаемой функции нужно выполнить преобразование

к

При равномерном квантовании по аргументу x*{tj)= Cii<fii{tj),.

*=о

В АИС, так же как и в других ИС, информационные операции могут вы подняться последовательным, параллельным или смешанным способами. Аппроксимирующие измерительные системы могут реализоваться с замкнутой или разомкнутой информационной обратной связью, в виде аналоговых или цифровых устройств.

При создании и использовании АИС приходится решать ряд специфи- Рис. И.5. Исходные функции ческих задач, к которым в первую очередь относятся выбор типа приближающего многочлена и определение его порядка, исходя из заданной погрешности аппроксимации.

Решение этих задач зависит от вида изучаемой исходной функции, заранее известной информации о ней, от цели измерения, метрологических требований к измерениям и т. д.

В качестве приближающих многочленов с базисными функциями ф(/) могут быть выбраны ряды Фурье, разложения Фурье -Уолша, Фурье -Хаара, многочлены Чебышева, Лагранжа, Лежандра, Лагерра и др. Основные данные о наиболее широко применяемых многочленах приведены в гл. 21.

Приведем примеры реализации АИС. Остановимся на использовании АИС при измерении коэффициентов разложения Фурье - Уолша распределенной в про-

х(в): x(t), x(l),M(tie(co,f(x)

-e:t,l,t,co,x,

лтранстве непрерывной функции х{1). Б этом важном для практики случае исходная величина воздействует в каждый момент на датчики, жестко закрепленные в узлах аппроксимации. Для первоначального рассмотрения можно принять, что в процессе измерения исследуемая функция не изменяется, координаты мест расположения датчиков известны с заданной точностью, а датчики воспринимают эту функцию в точках. Конечно, отступления от этих условий окажут .влияние на погрешность результата измерения, но это влияние может быть оценено особо.

Размещение датчиков должно быть таким, чтобы можно было описать .исходную функцию с заданной погрешностью по полученным дискретам. Расчет интервалов квантования может быть выполнен из соображений, приведенных в гл. 22. Допустим, что на интервале наблюдения расположено Л?=2 датчи-ков. Тогда имеется возможность реализовать алгоритм получения коэффициентов Фурье - Уолша по формуле

Cfe=(i/2 )2 (ofeC/).

Тде Wk {1}) - функция Уолша.

Аппроксимирующая измерительная система разомкнутого типа при использовании функций Уолша реализуется довольно просто.

Положим, необходимо произвести аппроксимацию пространственной кривой воспринимаемую четырьмя датчиками, с использованием разложения Фурье - Уолша. Матрица коэффициентов функций Уолша Wk (Ij) третьего по-.рядка и структуры аналоговой части АИС параллельного (а) и последователь-,ного (б) действия представлены на рис. П.6. В параллельной структуре показа-

.ны цепи, необходимые для получения по формуле Сь=(1/4) 2 (.h)(h)

коэффициентов Со .и С,. Поскольку функции Уолша принимают значения -fl 1ЯЛИ -1, то сопротивления равны между собой.

При последовательном получении коэффициентов Со и Ci алгоритм работы зыглядит следующем образом: при измерении 4Со

Ф(4Со, 1Го) {iix{hmix{h)]\\4xm\\i[x(u)]}

-tx{h)+x(k)] I(4Co);

при измерении 4Ci

Ф(4С ir,) {1[л;(/,)]1[д;(У]111[-л:(/з)]111[-л:(/4)]}Х Xl[x{h)+x{l2)-x(k)-x(U)] I(4C.).

Коэффициенты разложения Уолша при этом выдаются генератором G ФУ.

На выходе аналоговой части может быть произведен анализ значимости по-.лученных и устранение несущественных коэффициентов. Помимо этого, отбор .существенных коэффициентов может быть выполнен путем оценки погрешности восстановления с помощью сравнения восстановленной и исходной функций и .решения о значимости полученных коэффициентов.

Если исходная функция описывается многочленом высокого порядка, то .-имеется возможность >многократного использования АИС на отдельных участках

1 Z 3

>

-LiCB=x(li)+x(l2)+X(l3)+X(li,)

> -i,c,=x(li)+x(lz)-x(l3)-x(l)

Рис. 11.6. АИС с параллельным и последовательным получением коэффициентов Фурье - Уолша:

а - параллельное соединение; б - последовательное соединение; в - таблица функций Уолша

существования функции и сшивания кусочного описания в единое выражение. Возможность перехода к единому выражению при использовании функций Уолша определяется тем, что функции Уолша для удвоенного интервала увеличивают порядковый номер, а коэффициенты при таком сшивании могут быть получены в виде С-(С'-\-С )/2. Это достаточно наглядно может быть проиллюстрировано с использованием матрицы коэффициентов Уолша. Положим, определены коэффициенты Cm и Сц, а также Coi и Сц для двух отрезков [О, 0,5] и [0,5, 1], содержащих по два датчика (1 и 2, 3 и 4). Тогда для отрезка [0,1] получается

Со= (Со,+Со2) /2; С, = (Со,-С.о2) /2; C2=(Ci,-fC,2)/2; Сз=(С„-С,2)/2.

Действительно, если

Co,=0.5[x( ,)-fx( 2)]; Co2=0,5[x( 3)+-v( 4)]; С„=0,5[х(г,)-х(У];

Со=0,25 [X (г,) (h)-{-x (h) +х ih)]; С,=0,25 [X (h)-\-x (h) -X (h) -X (/4) ]; C2=0,25 [X (Z,) -.V +x (is) -X ( 4) ]; Сз=0,25[х (l{)-x (h)-x (h)-\-x (h) ].

После выполнения таких операций имеется возможность вновь оценить значимость и отфильтровать несущественные коэффициенты.

В Новосибирском электротехническом институте [11.7] были изготовлены и использованы в различных целях АИС: для работы с четырьмя термопарами (20 тыс. коэффициентов разложения Фурье - Уолша в секунду, +0,4 7о); для анализа периодических сигналов с частотой 10, 100, 1000, 10 000 Гц, ±1 %; для работы с четырьмя тензодатчиками (использовались многочлены Чебышева и разложение Фурье - Уолша, производилось одновременное измерение четырех коэффициентов, +0,5%); для работы с 64 тензодатчиками (получались 64 коэффициента ряда Фурье, разложения Фурье - Уолша, Фурье - Хаара и Чебышева); для работы с тензодатчиками с применением микро-ЭВМ С5-11, Электроника-60 . Кроме того, было изготовлено несколько генераторов сигналов заданной формы.

К основным областям применения АИС и восстанавливающих (синтезирующих) устройств относятся измерение статистических характеристик случайных процессов (см. гл. 12) и характеристик нелинейных элементов, сжатие радиотелеметрической информации и инфор.мации прн анализе изображений, фильтрация-восстановление фушщии без некоторых коэффициентов [11.8], генерация сигналов заданной формы

Представляет интерес использование АИС для организации контроля состояния исходной функции и для распознавания образов по коэффициентам разложения.

Глава 12

СТАТИСТИЧЕСКИЕ ИЗМЕРИТЕЛЬНЫЕ СИСТЕМЫ

12.1. особенности измерения статистических характеристик случайных процессов

Статистический анализ случайных величин и процессов широко применяется во всех отраслях науки и техники.

Для специалистов ИИТ необходимо не только уметь пользоваться статистическими характеристиками при проектировании и анализе погрешностей технических средств, но и знать методы и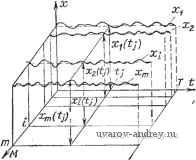

Рис. 12.1. процесса

Реализации случайного

принципы построения аппаратуры, предназначенной для экспериментального измерения таких характеристик. Ввиду особой важности статистических измерительных систем здесь целесообразно привести в весьма сжатом виде основные сведения о принципах построения таких систем и дать примеры их реализации.

Для более глубокого изучения теории статистических измерений, методов и средств измерения статистических характеристик специалистам в области ИИТ можно рекомендовать в первую очередь [12.1, 12.2].

Для изучения материала по статистическим измерениям от читателя требуется твердое знание и понимание основ теории вероятностей в объеме [12.3].

При экспериментальном измерении характеристик случайных процессов имеется возможность оперировать с временной реализацией Xi{t), ансамблем реализаций {Xi{t)}i=i2,....m при О^Г или ансамблем реализаций {Xi{tj)}i=i,2взятых в определенный момент времени tj (рис. 12.1).

Нужно подчеркнуть, что рассмотренное далее приложимо и к анализу случайных функций, у которых в качестве аргумента могут быть время, пространственные координаты и т. п. Заметим, что при фиксированных значениях аргумента значения функции - случайные величины.

Случайные процессы могут быть заданы в непрерывном или в квантованном по времени виде. В последнем случае функция задается выборкой дискретных значений непрерывной функции, взятых через определенный интервал времени А^.

При анализе ансамбля реализаций, конечно, получается наиболее полная информация о случайном процессе. В ряде практически важных случаев можно ограничиться определением характеристик случайного процесса по одной его роализации или по ансамблю значений-это оказывается возможным, если случайный процесс является стационарным и эргодическим.

В дальнейшем остановимся на экспериментальном измерении характеристик стационарных эргодических процессов [12.4].

Полученные в результате измерения эмпирические характеристики случайных процессов принято называть оценками истинных характеристик Q*. Эти оценки сами по себе являются случайными величинами. Поэтому при планировании статистического измерительного эксперимента необходимо решать задачи получения оценок характеристик с заданной погрешностью при ограничениях, накладываемых на объем исходных данных, на время измерения, . а. возможности аппаратуры и т. п.

Как известно, оценки характеристик должны быть состоятельными, несмещенными и эффективными. Состоятельной называется оценка, вероятность отклонения значения которой от оцениваемой величины прн увеличении объема статистического материала N стремится к нулю, т. е. P{\Qif*-Q\e}=0. Оценка называется

несмещенной, если разность ее математического ожидания и истинного значения оцениваемой величины приближается к нулю, т. е. фактически при этом требуется, чтобы отсутствовала систематическая ошибка. Смещение оценки Q* определяется как AQ*= =M[Q*]-Q. Оценка называется эффективной, если несмещенная оценка обладает наименьшей дисперсией: minD[Q*] = =minM{M[Q*]-Q}2. Погрешность оценки Q* обычно определяется доверительной вероятностью и и доверительным интервалом Q±e:

Р (Q*-e<Q<Q*+8) =и.

Типовой алгоритм измерения характеристик стационарного' случайного процесса по его реализации x{t) может быть представлен Б следующем виде:

Q=M{HMt)]},

гд H[x{t)]-соответствующее данной оценке преобразование исследуемого процесса. Если x{t) представлено в виде непрерывной функции, то типовой алгоритм реализуется в интегральном

виде: Q * [x(f)] если же исследуемый процесс пред-

ставлен в виде N дискрет, то

где At-интервал равномерного квантования x{t) по времени. Результат преобразования Нф[л:(<)] при измерении математического ожидания равен Ylm[x{t)]=x{t), дисперсии - Ял[л:()] =[x{t) - -MxV, дискрет корреляционной функции HR[x{t)] = [x{t) - -Мх] [x{t+x)-Mx] и т. д.

Большинство характеристик, получаемых по описанному алгоритму, состоятельны, несмещенны и эффективны. Исключение составляет оценка дисперсии, и для устранения смещенности она должна быть представлена в виде

i [x{ii)-MxYlN [NUN-I)]. ./=1

Основными источниками методической погрешности при реализации этого алгоритма являются конечное время анализа T=NAt или конечный объем выборки N=TflS.t, квантование хЩ

по уровню и способ построения статистических функций по измеренным их дискретам.

Если задача статистических измерений заключается в получении параметров статистических функций, к которым относятся законы распределения вероятностей, корреляционные и спектральные функции, то их определение может быть также реализовано через измерение коэффициентов аппроксимирующих многочленов

к

с получением оценки изучаемой функции Q* = 2 Ct).

Основными источниками методических погрешностей в этом случае будут конечное число членов разложения и, как и в предыдущем способе, конечное время анализа или конечный объем выборки.

Чаще всего при статистическом анализе используются законы распределения вероятностей и моментные характеристики, корреляционные и спектральные функции.

Перейдем к рассмотрению структур и алгоритмов статистических измерительных систем, предназначенных для измерения законов распределения вероятностей, корреляционных и спектральных функций. Средства и алгоритмы измерения математического ожидания и дисперсии читателям предлагается изучить по [12.2].

Считаем полезным привести соотношения, необходимые для ориентировочного определения объемов выборок при измерении Мх и Dx. При измерении Мх некоррелированных выборок (А^>Ткор) otAX {1/N) {Dx/Mx)=x/N где Ткор-интервал корреляции, ам-средняя квадратическая погрешность измерения сред< него значения, %-коэффициент изменчивости. Конечно, это выражение справедливо при Мх=фО. Средняя квадратическая погрешность определения Dx связана с объемом некоррелированных выборок так:

oD(v2/N. \

Подчеркнем, что приведенные соотношения пригодны для грубых, ориентировочных расчетов. При слабо коррелированных выборках объем N должен быть увеличен.

12.2. СИСТЕМЫ ДЛЯ ИЗМЕРЕНИЯ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ СЛУЧАЙНЫХ ПРОЦЕССОВ

Одномерный интегральный закон, или интегральная функция распределения вероятностей, определяется вероятностями нахождения исследуемого процесса ниже уровня х, который может изменяться от-оо до -foo: F{x)=p[~oox(t) х] (рис. 12.2). По определению F(-oo)-0 и /(-fc )=I.